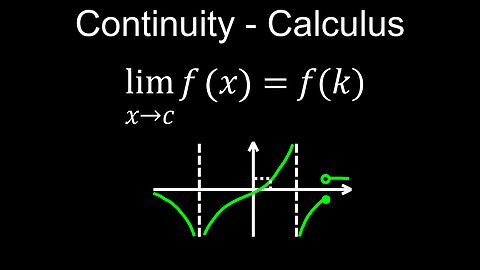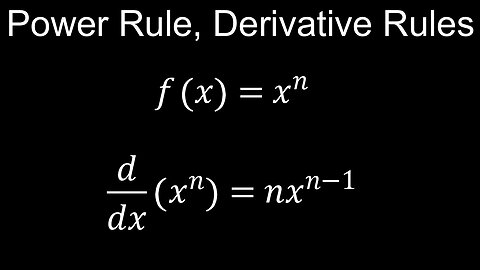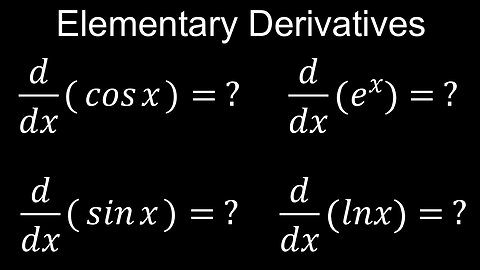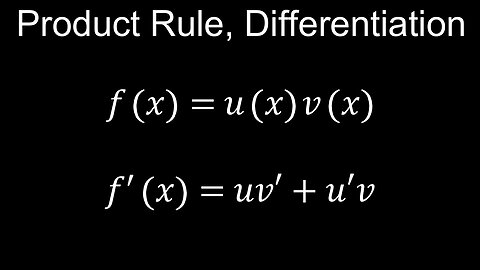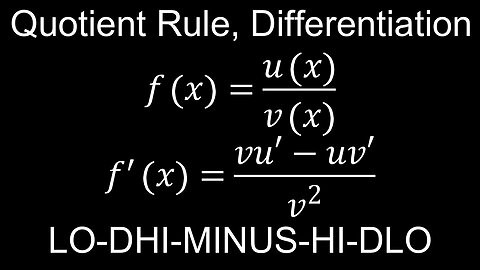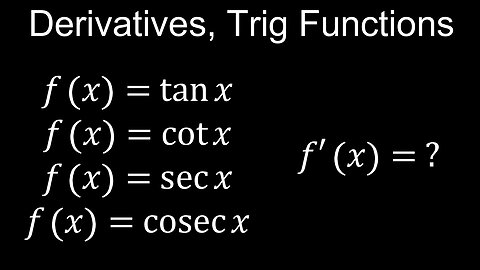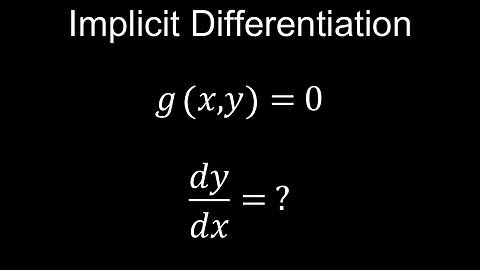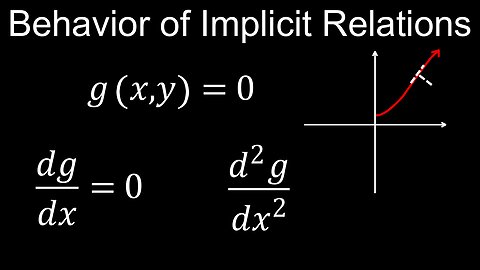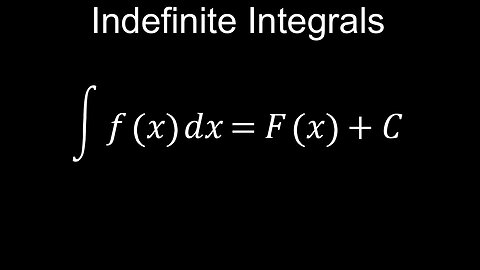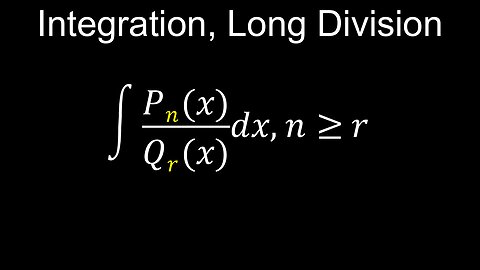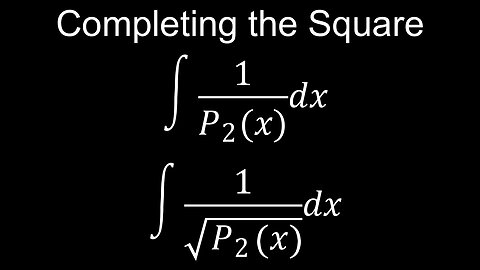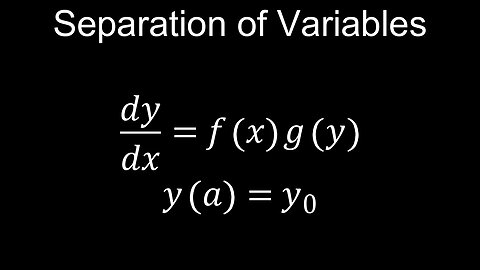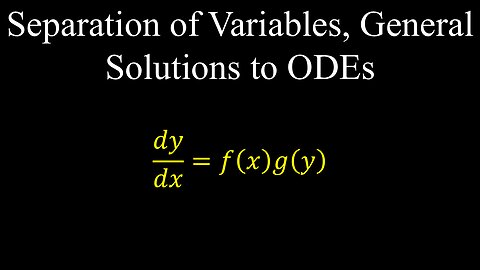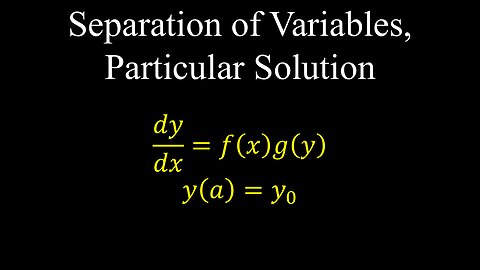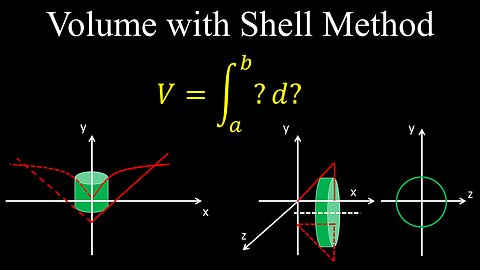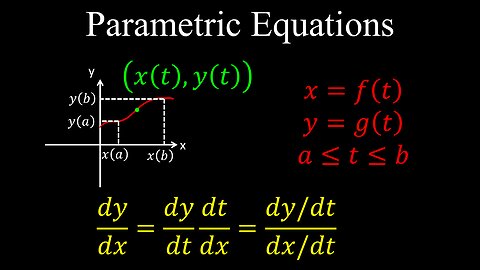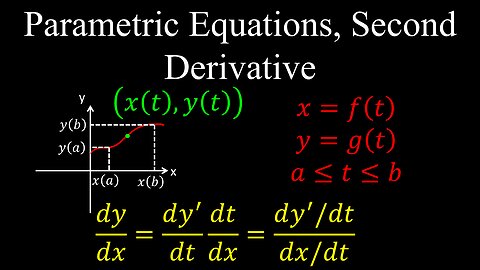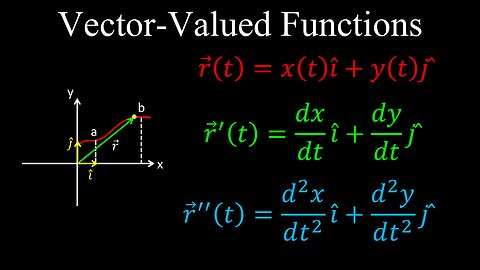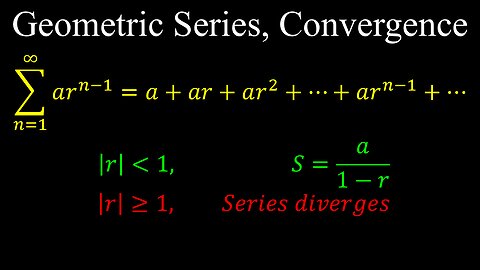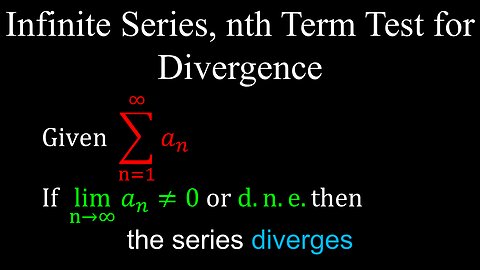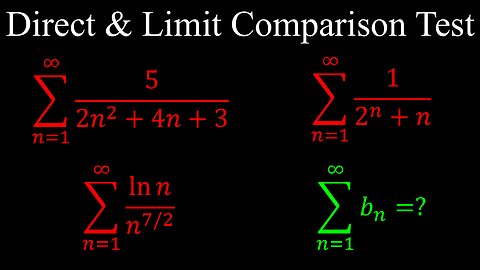Premium Only Content
Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
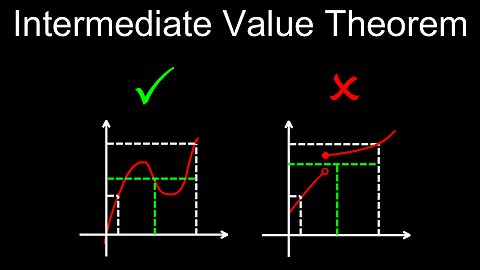
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
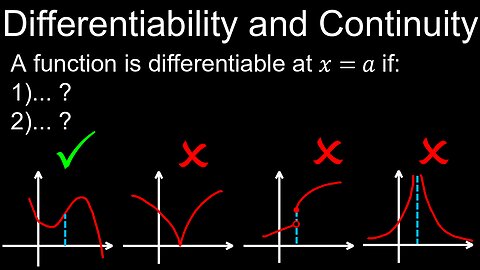
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
Derivative Rules, Power Rule for Differentiation - Calculus
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
Product Rule, Differentiation, Basic Proof, Examples - Calculus
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
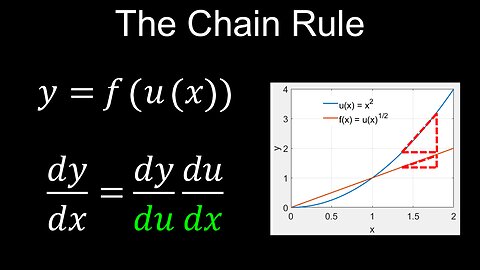
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
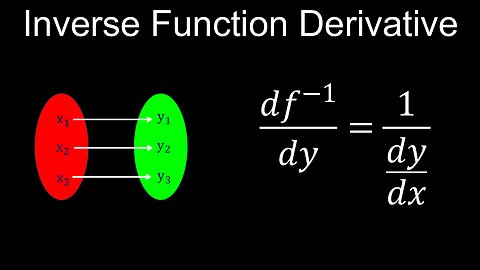
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
Derivatives in Context, Interpretation, Examples - Calculus
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
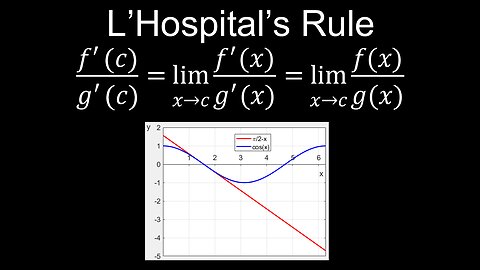
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
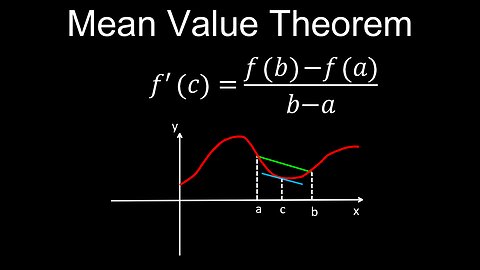
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
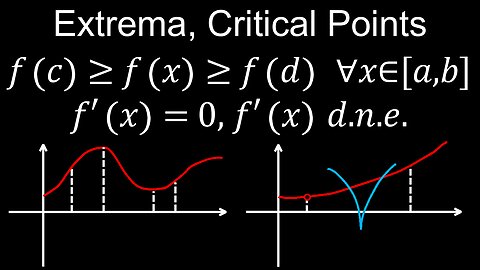
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
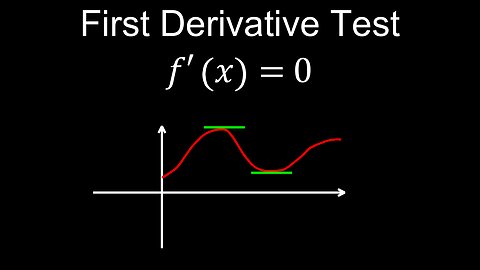
First Derivative Test, Local Extrema, Examples - Calculus
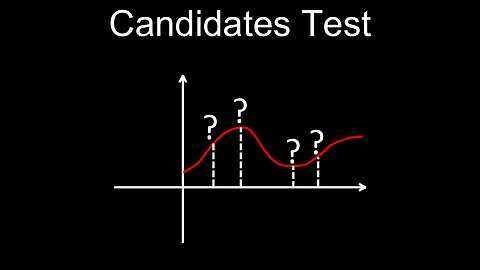
Candidates Test, Global Extrema, Example - Calculus
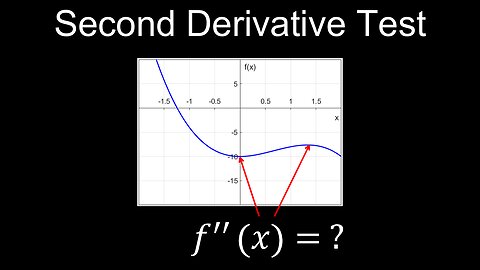
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
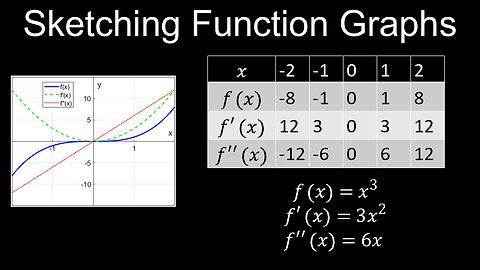
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
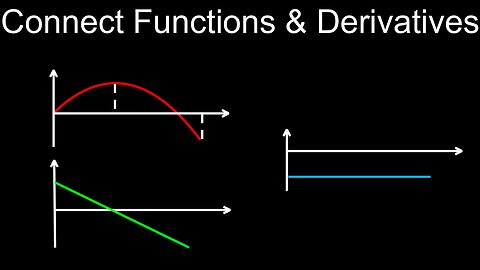
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
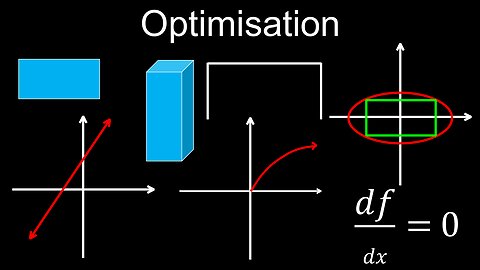
Solving Optimisation Problems, Differentiation, Examples - Calculus
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
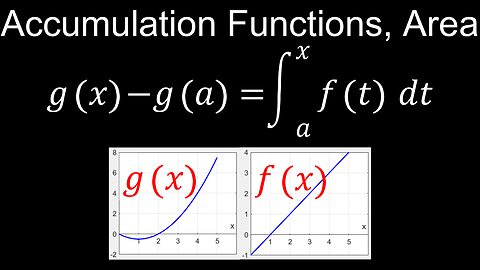
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
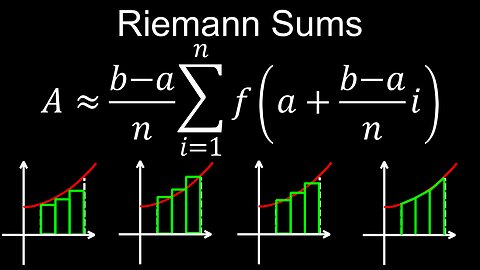
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
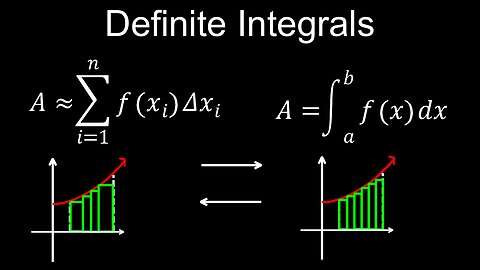
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
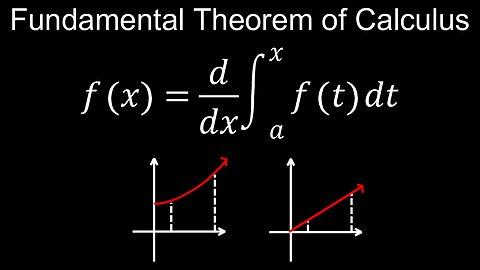
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by Parts, Formula, Rule, Example, Order - Calculus
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
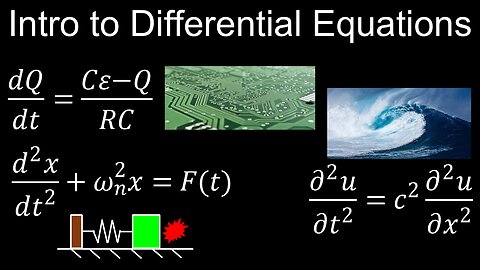
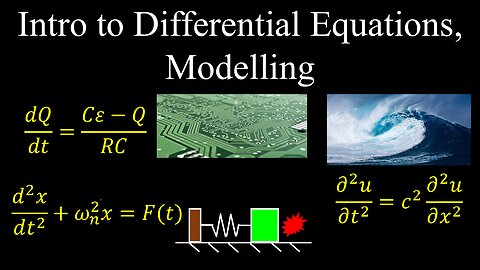
Intro to Differential Equations, Modelling, Worksheet, Example - Calculus
Verifying Solutions to Differential Equations, Examples - Calculus
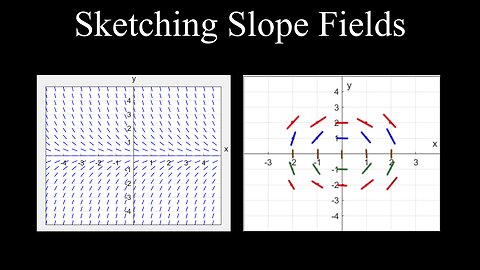
Sketching Slope Fields and Solution Curves Explained, Differential Equations, Example - Calculus
Euler's Method for Solving Differential Equations Explained, Example - Calculus
Separation of Variables Method, Differential Equations, Integration, Examples - Calculus
Exponential Models with Differential Equations, Population Growth, Examples - Calculus
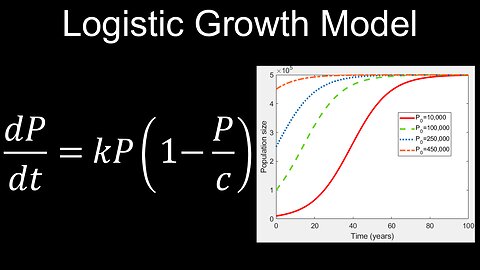
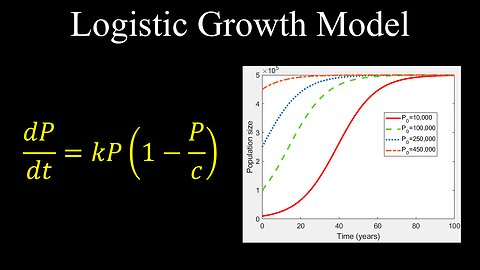
Logistic Growth Differential Equation, Model, Example - Calculus
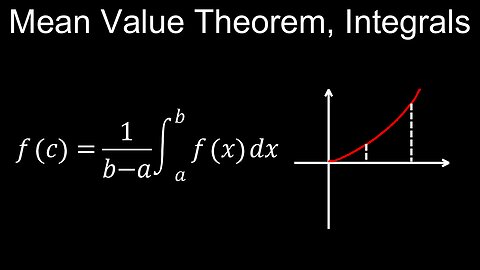
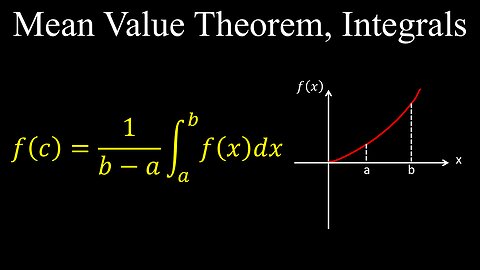
Mean Value Theorem for Integrals, Visual Proof, Examples, Practice Problems - Calculus
Connecting Position, Velocity, Acceleration of Functions, Integrals, Straight Line Motion - Calculus
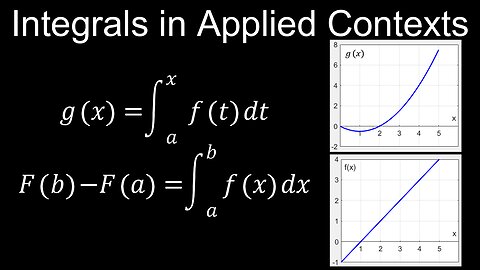
Interpreting Definite Integrals in Applied Contexts Explained, Examples - Calculus
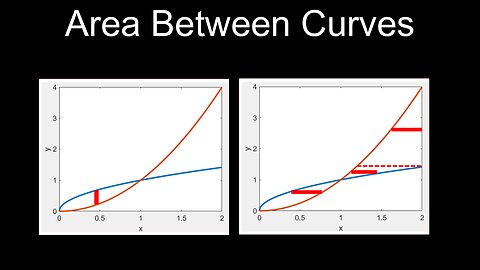
Area Between Two Curves, Integration, With Respect to x and y, Practice Problems - Calculus
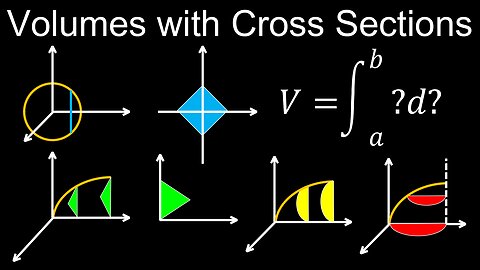
Volumes with Cross Sections, Squares, Rectangles, Triangles and Semicircles - Calculus
Volume with the Disc Method, Solids of Revolution, Examples, Practice Problems - Calculus
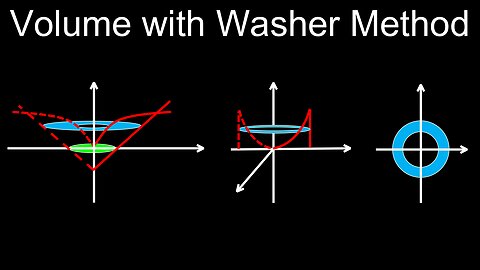
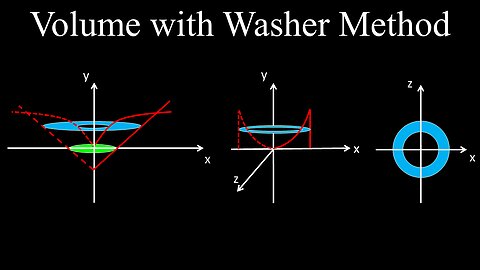
Volume with the Washer Method, Formula, Examples, Practice Problems - Calculus
Arc Length Integral Formula, Distance, Problems and Solutions - Calculus
Intro to Differential Equations, Modelling - Calculus
Verifying Solutions to Differential Equations - Calculus
Sketching Slope Fields, Differential Equations - Calculus
Sketching Solution Curves, Slope Fields - Calculus
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
Separation of Variables, General Solution, ODEs - Calculus
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
Exponential Models, Growth, Decay, Differential Equations - Calculus
Logistic Growth Model, Differential Equations - Calculus
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
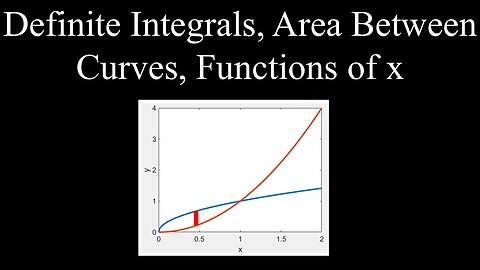
Definite Integrals, Area Between Curves, Functions of x - Calculus
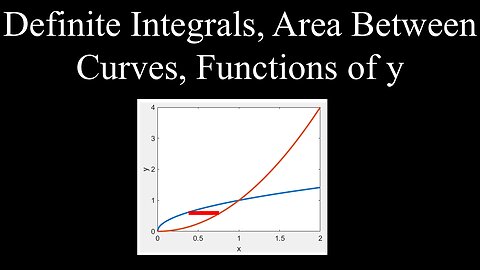
Definite Integrals, Area Between Curves, Functions of y - Calculus
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
Volume with the Disk Method, Revolving Around other Axes - Calculus
Washer Method to Find the Volume of a Revolved Solid - Calculus
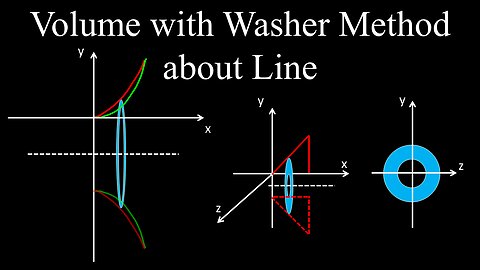
Volume with the Washer Method, Revolved Solid Around Line - Calculus
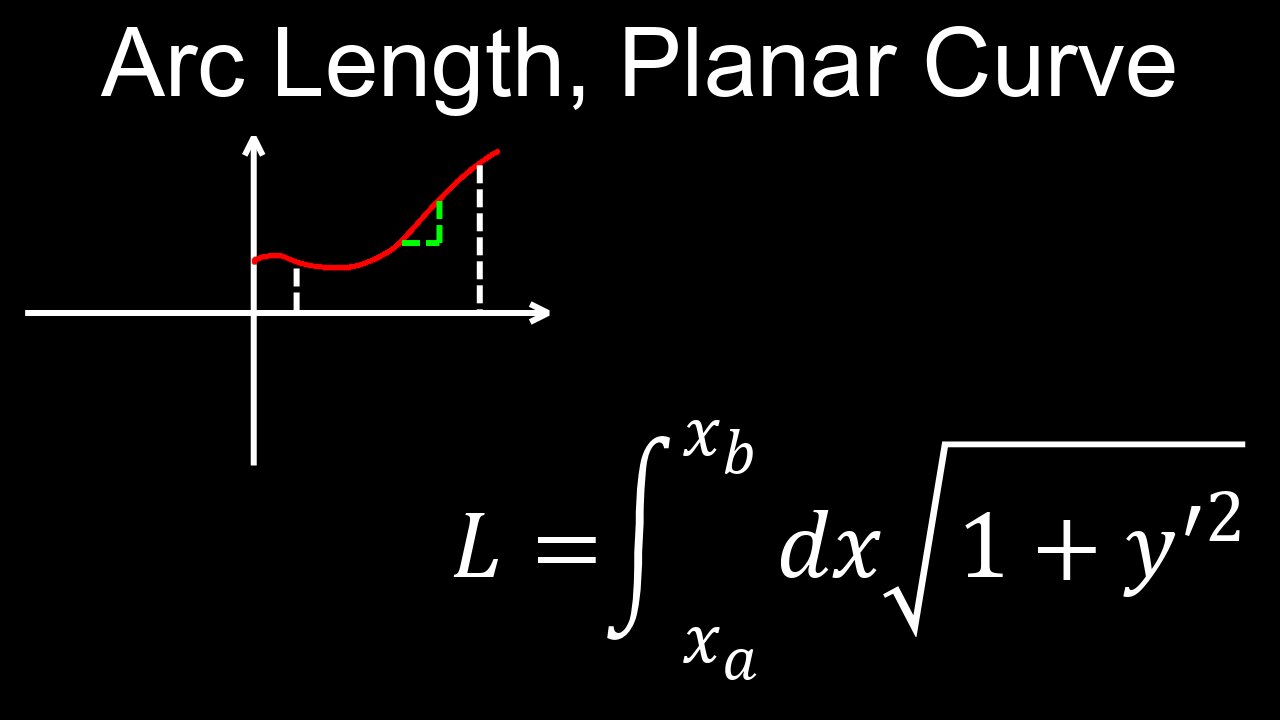
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
Parametric Equations, Definition, Differentiation - Calculus
Parametric Equations, Second Derivative - Calculus
Parametric Curve, Arc Length, Distance - Calculus
Vector-Valued Functions, Differentiation, Examples - Calculus
Vector-Valued Function, Integration - Calculus
Vector-Valued Functions and Motion in 2D Space - Calculus
Polar Coordinates, Polar Curves, Differentiation - Calculus
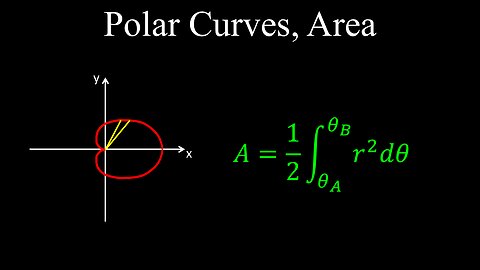
Polar Curve, Area of Region, Integration - Calculus
Polar Curve, Area of Region between Two Curves, Examples - Calculus
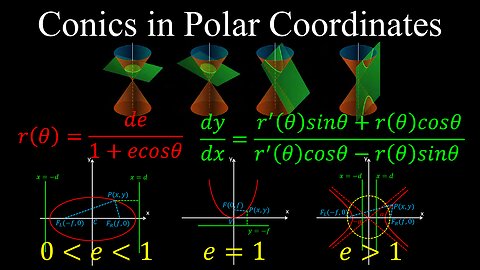
Conics in Polar Coordinates, Derivatives, Example - Calculus
Infinite Sequence, Definition, Representations, Convergence - Calculus
Infinite Series, Definition, Partial Sum, Convergence - Calculus
Geometric Series, Sum, Convergence - Calculus
nth Term Test, Divergence, Infinite Series, Examples - Calculus
Integral Test, Convergence, Infinite Series, Example - Calculus
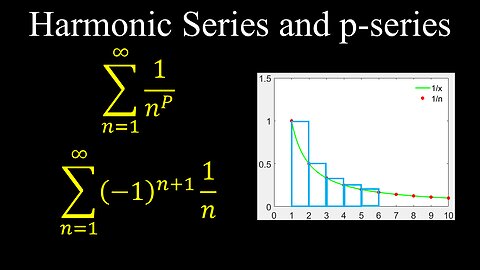
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
Alternating Series Test, Infinite Series - AP Calculus BC
Ratio Test, Infinite Series, Convergence, Examples - Calculus
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
Arc Length Integral Formula, Distance, Problems and Solutions - Calculus
In calculus, arc length is the length of a curve between two points, calculated by integrating a formula that sums infinitesimal segments of the curve. For a smooth function \(y=f(x)\) over an interval \([a,b]\), the arc length \(L\) is found by integrating the square root of \((1+[f^{\prime }(x)]^{2})\) with respect to \(x\) from \(a\) to \(b\): \(L=\int _{a}^{b}\sqrt{1+[f^{\prime }(x)]^{2}}\,dx\).
💡Deriving the Arc Length Formula
The formula is derived by approximating the curve with a series of tiny line segments and finding the limit as the number of segments approaches infinity.
• Divide the curve: into \(n\) small segments.
• Approximate the length: of each segment with the hypotenuse of a right triangle, where the legs are the change in \(x\) (\(\Delta x\)) and the change in \(y\) (\(\Delta y\)).
• Use the Pythagorean theorem: The length of each segment is \(\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}\).
• Rewrite: this in terms of the derivative \(\frac{dy}{dx}\):
\(\sqrt{(\Delta x)^{2}(1+(\frac{\Delta y}{\Delta x})^{2})}=\Delta x\sqrt{1+(\frac{dy}{dx})^{2}}\).
• Sum the lengths: of all these segments to approximate the total arc length:
\(\sum \Delta x\sqrt{1+(\frac{dy}{dx})^{2}}\).
• Take the limit: as \(\Delta x\) approaches 0, transforming the sum into a definite integral:
\(\int _{a}^{b}\sqrt{1+(\frac{dy}{dx})^{2}}\,dx\).
💡Formulas for Different Cases
• For \(y=f(x)\): If the curve is defined as a function of \(x\), the arc length \(L\) from \(x=a\) to \(x=b\) is:
\(L=\int _{a}^{b}\sqrt{1+\left(\frac{dy}{dx}\right)^{2}}\,dx\quad \text{or}\quad L=\int _{a}^{b}\sqrt{1+[f^{\prime }(x)]^{2}}\,dx\).
For \(x=g(y)\): If the curve is defined as a function of \(y\), the arc length \(L\) from \(y=c\) to \(y=d\) is:
\(L=\int _{c}^{d}\sqrt{1+\left(\frac{dx}{dy}\right)^{2}}\,dy\quad \text{or}\quad L=\int _{c}^{d}\sqrt{1+[g^{\prime }(y)]^{2}}\,dy\).
• For Parametric Curves: For a curve defined by parametric equations \(x=x(t)\) and \(y=y(t)\), the arc length \(L\) from \(t=a\) to \(t=b\) is:
\(L=\int _{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\,dt\).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1GQtYzPXeZpvnm7EdpOAPfEyr-VSltAse/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1urkbDfPaDPsymE8T58TZZJHgeUw-P-qx/view?usp=drive_link
💡Chapters:
00:00 Arc length integral
02:04 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
![[Ep 794] Epstein Act | MTG 2.0 [Liz Cheney?] | Crooks, Furries, & Social Media | Guest – Sam Anthony](https://1a-1791.com/video/fww1/1b/s8/1/u/D/2/A/uD2Az.0kob-small-Ep-794-Epstein-Act-MTG-2.0-.jpg) LIVE
LIVE
The Nunn Report - w/ Dan Nunn
1 hour ago[Ep 794] Epstein Act | MTG 2.0 [Liz Cheney?] | Crooks, Furries, & Social Media | Guest – Sam Anthony
142 watching -
 1:06:52
1:06:52
DeVory Darkins
3 hours agoBREAKING: Congress issue MAJOR EPSTEIN Update as MTG goes OFF THE RAILS
111K106 -
 2:06:23
2:06:23
Side Scrollers Podcast
5 hours agoStreamer Awards WRECKED + Cloudfare OUTAGE + AI LOVED ONES?! + More | Side Scrollers
31.9K3 -
 1:57:30
1:57:30
Steven Crowder
6 hours agoSteven Crowder is a Deep State Agent
552K436 -
 1:04:17
1:04:17
Sean Unpaved
4 hours agoJames Franklin Is Going To REVIVE Virginia Tech! | UNPAVED
28.4K2 -
 LIVE
LIVE
Viss
7 hours ago🔴LIVE - Completing Quests & Annihilating All in Our Path! - Arc Raiders!
86 watching -
 53:51
53:51
The Rubin Report
5 hours agoBill Maher Obliterates Patton Oswalt’s Liberal Bubble in Only 2 Minutes
62.3K71 -
 LIVE
LIVE
LumpyPotatoX2
5 hours agoWhere Winds Meet: Just Petting Kitties - Made in China
39 watching -
 LIVE
LIVE
ReAnimateHer
21 hours ago $1.09 earnedDBD Shenanigans
38 watching -
 1:08:01
1:08:01
iCkEdMeL
4 hours ago $2.22 earned🚨Mom Gives Birth on Highway After Kicked Out of Hospital?!
28.9K12