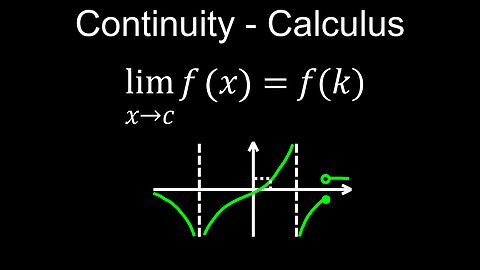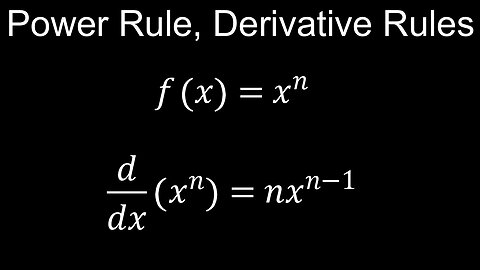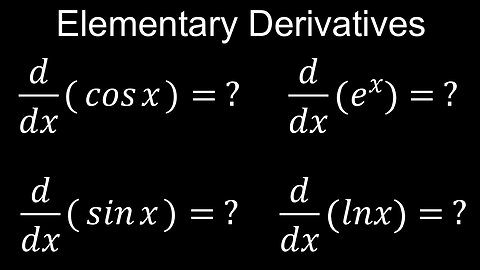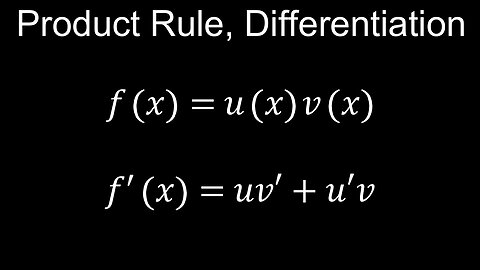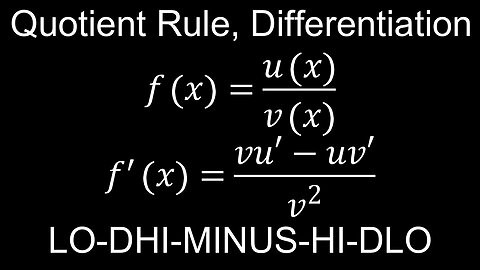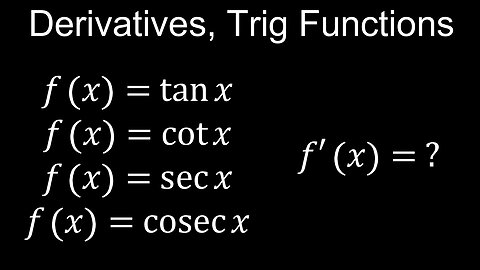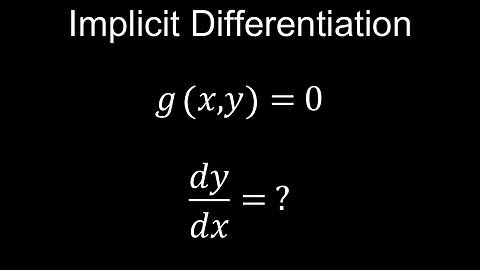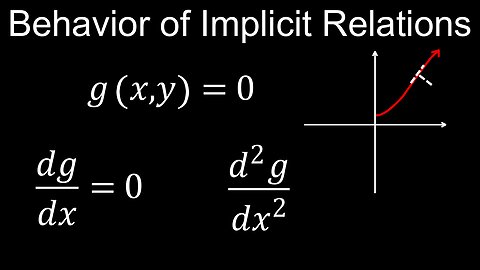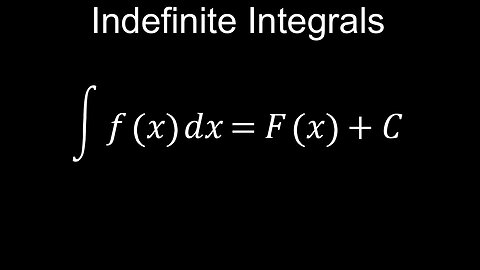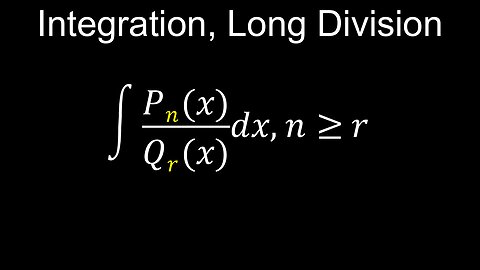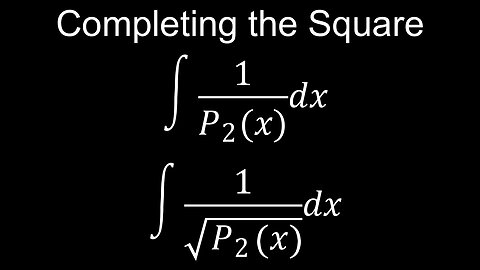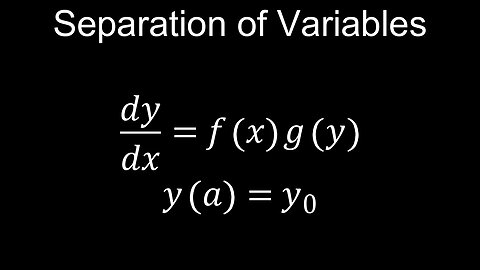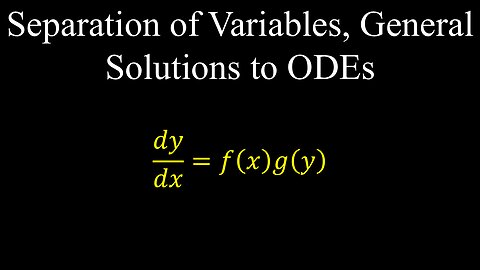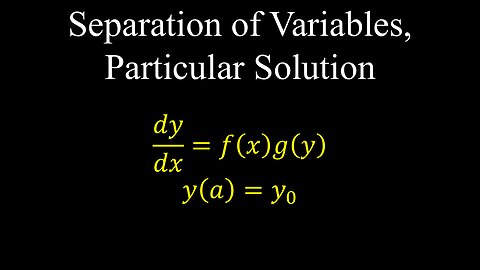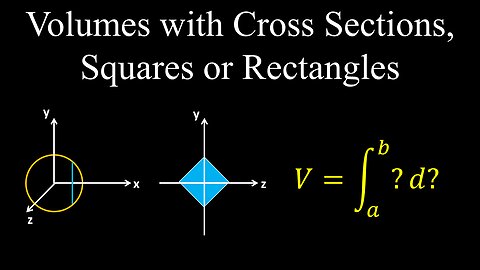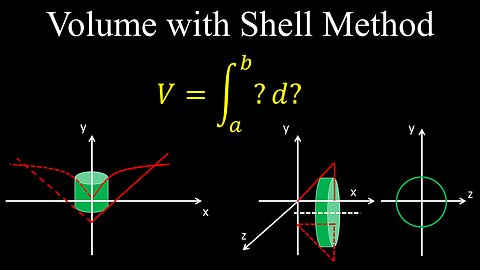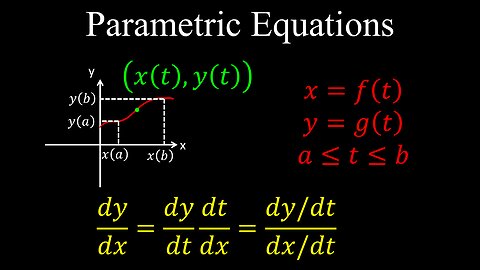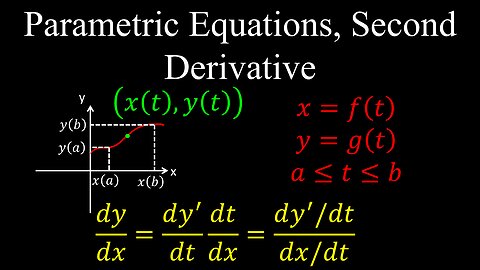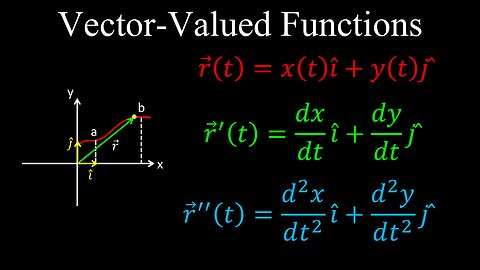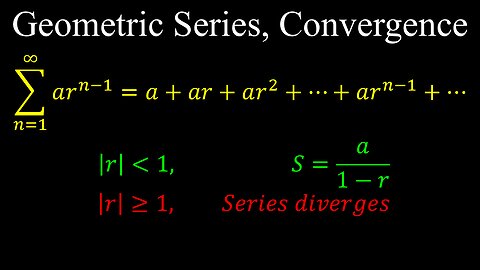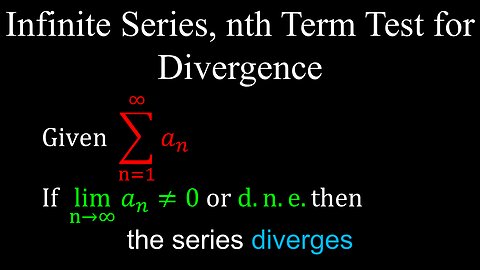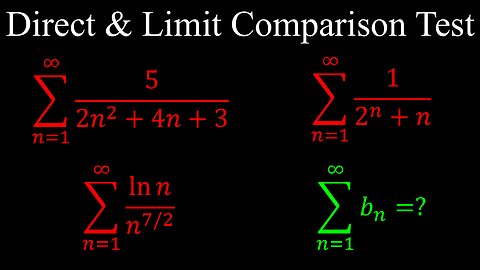Premium Only Content
Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
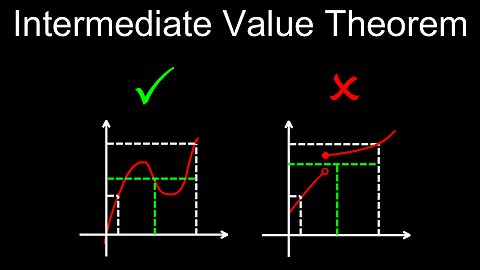
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
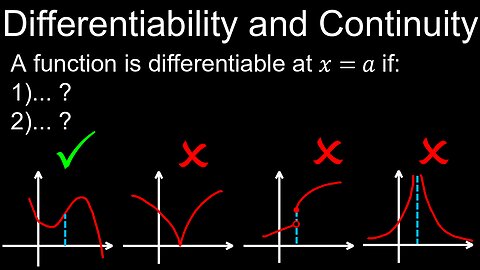
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
Derivative Rules, Power Rule for Differentiation - Calculus
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
Product Rule, Differentiation, Basic Proof, Examples - Calculus
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
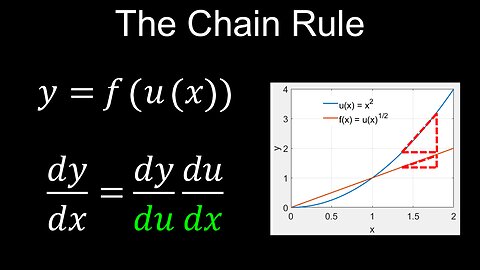
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
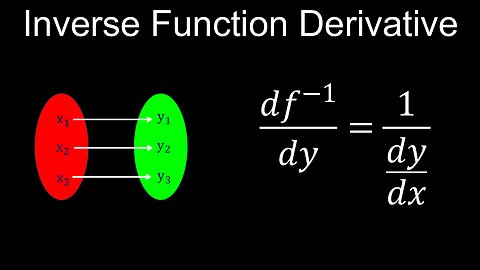
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
Derivatives in Context, Interpretation, Examples - Calculus
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
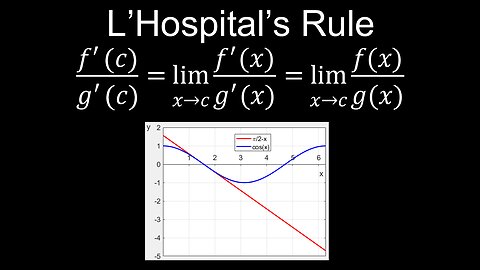
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
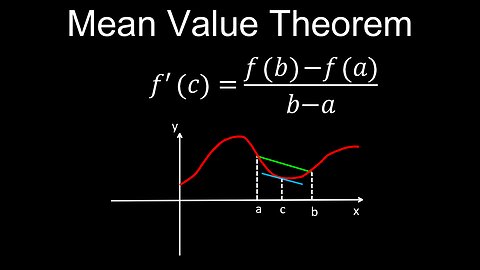
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
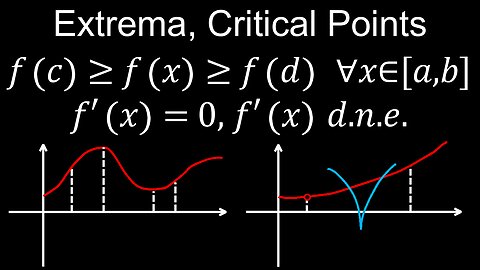
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
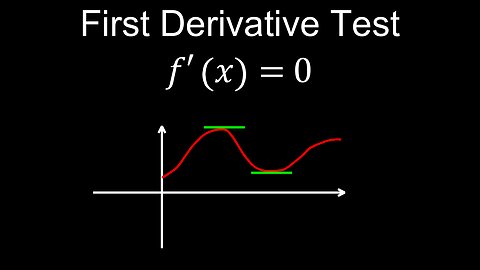
First Derivative Test, Local Extrema, Examples - Calculus
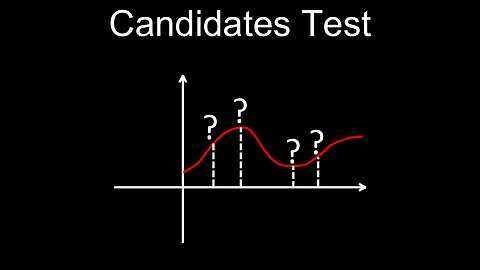
Candidates Test, Global Extrema, Example - Calculus
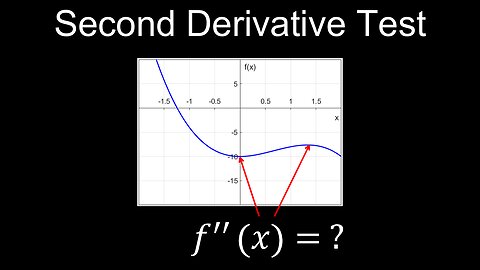
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
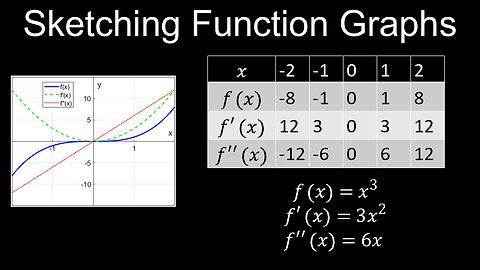
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
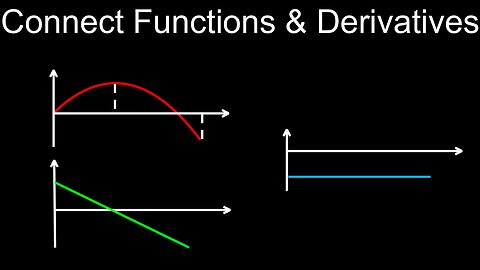
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
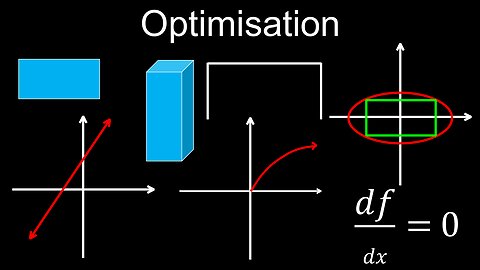
Solving Optimisation Problems, Differentiation, Examples - Calculus
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
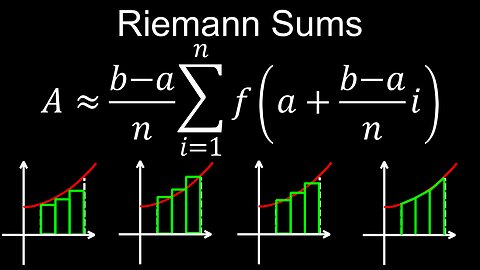
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
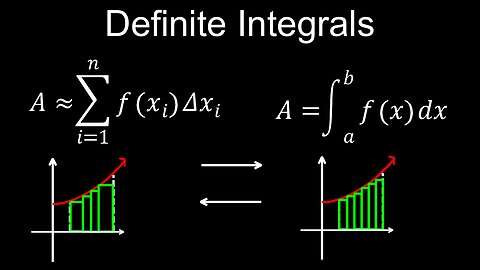
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
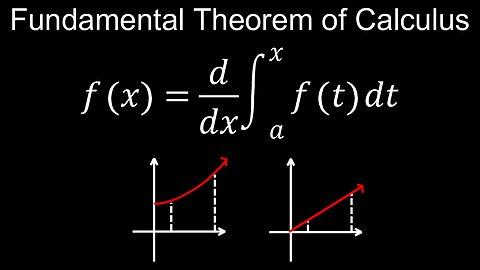
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
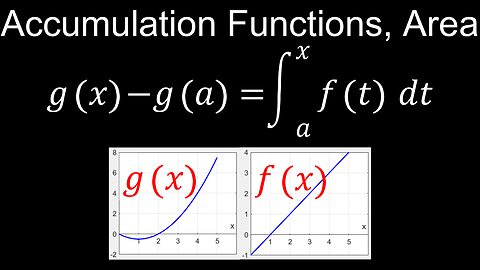
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by Parts, Formula, Rule, Example, Order - Calculus
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
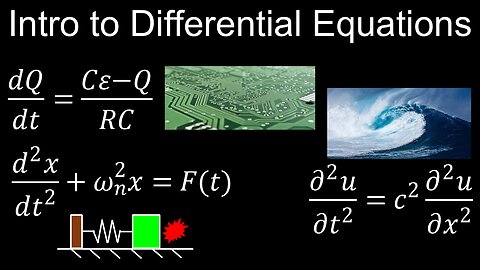
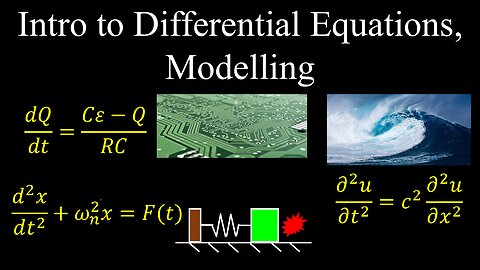
Intro to Differential Equations, Modelling, Worksheet, Example - Calculus
Verifying Solutions to Differential Equations, Examples - Calculus
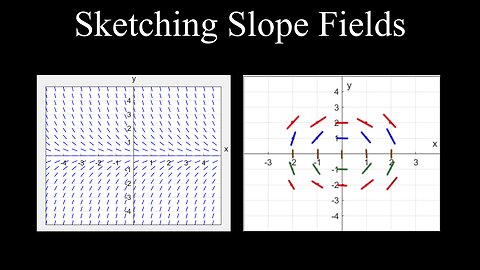
Sketching Slope Fields and Solution Curves Explained, Differential Equations, Example - Calculus
Euler's Method for Solving Differential Equations Explained, Example - Calculus
Separation of Variables Method, Differential Equations, Integration, Examples - Calculus
Exponential Models with Differential Equations, Population Growth, Examples - Calculus
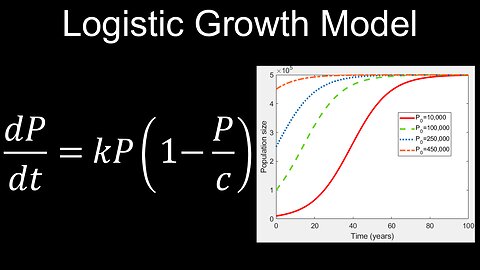
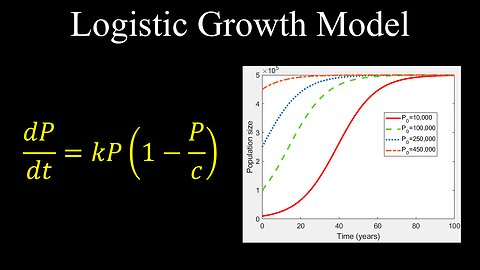
Logistic Growth Differential Equation, Model, Example - Calculus
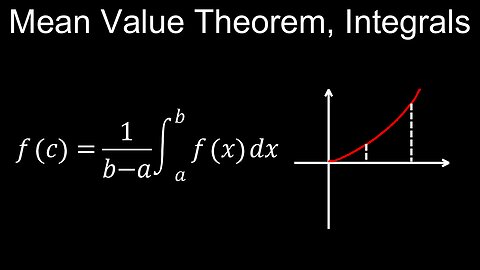
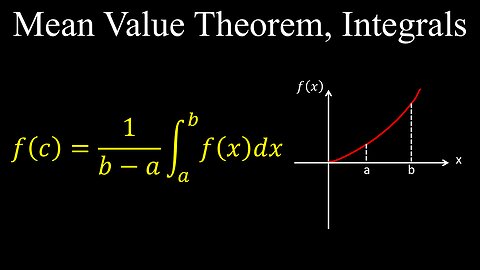
Mean Value Theorem for Integrals, Visual Proof, Examples, Practice Problems - Calculus
Connecting Position, Velocity, Acceleration of Functions, Integrals, Straight Line Motion - Calculus
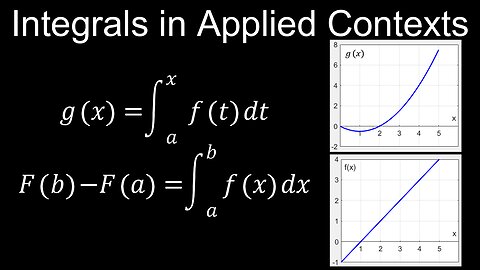
Interpreting Definite Integrals in Applied Contexts Explained, Examples - Calculus
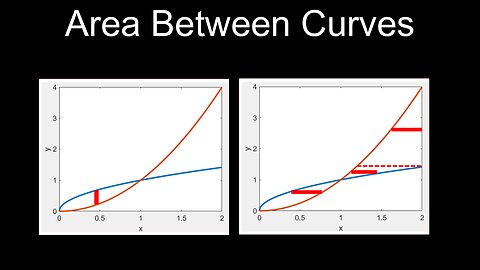
Area Between Two Curves, Integration, With Respect to x and y, Practice Problems - Calculus
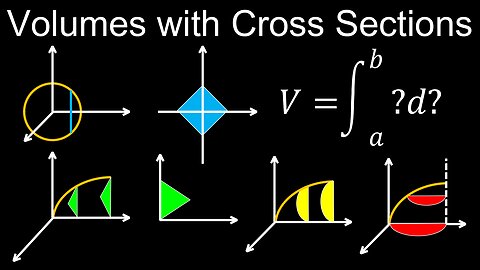
Volumes with Cross Sections, Squares, Rectangles, Triangles and Semicircles - Calculus
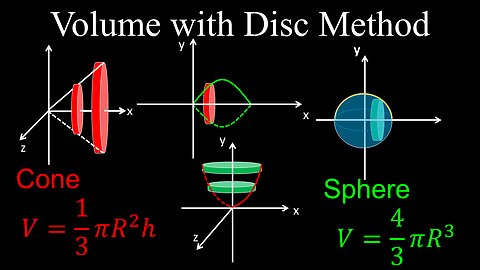
Volume with the Disc Method, Solids of Revolution, Examples, Practice Problems - Calculus
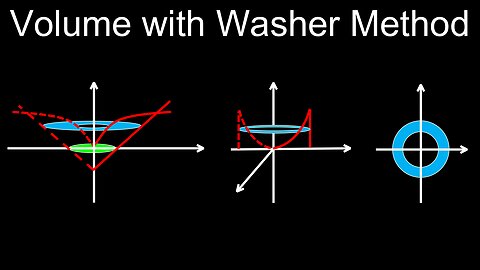
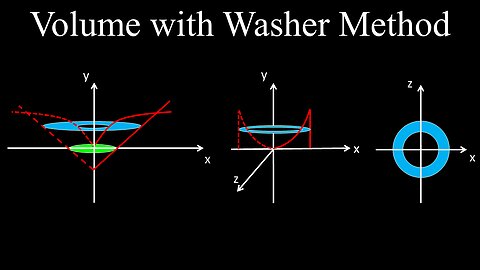
Volume with the Washer Method, Formula, Examples, Practice Problems - Calculus
Intro to Differential Equations, Modelling - Calculus
Verifying Solutions to Differential Equations - Calculus
Sketching Slope Fields, Differential Equations - Calculus
Sketching Solution Curves, Slope Fields - Calculus
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
Separation of Variables, General Solution, ODEs - Calculus
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
Exponential Models, Growth, Decay, Differential Equations - Calculus
Logistic Growth Model, Differential Equations - Calculus
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
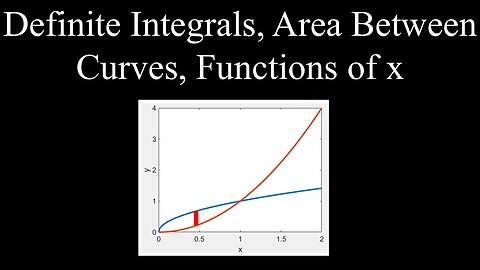
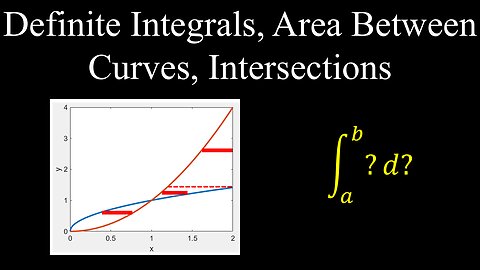
Definite Integrals, Area Between Curves, Functions of x - Calculus
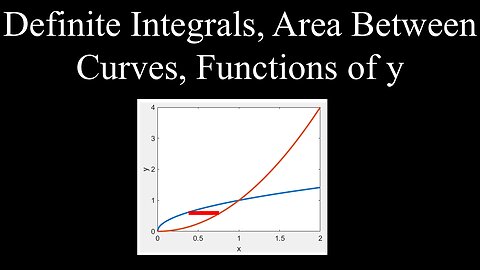
Definite Integrals, Area Between Curves, Functions of y - Calculus
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
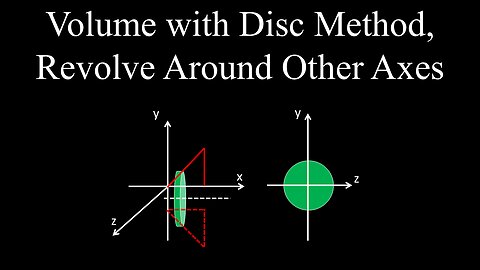
Volume with the Disk Method, Revolving Around other Axes - Calculus
Washer Method to Find the Volume of a Revolved Solid - Calculus
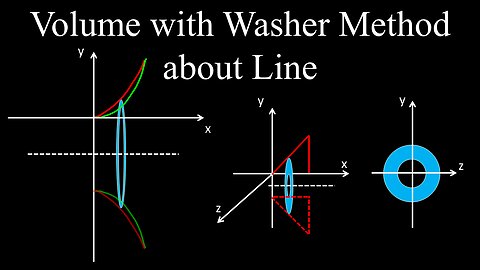
Volume with the Washer Method, Revolved Solid Around Line - Calculus
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
Parametric Equations, Definition, Differentiation - Calculus
Parametric Equations, Second Derivative - Calculus
Parametric Curve, Arc Length, Distance - Calculus
Vector-Valued Functions, Differentiation, Examples - Calculus
Vector-Valued Function, Integration - Calculus
Vector-Valued Functions and Motion in 2D Space - Calculus
Polar Coordinates, Polar Curves, Differentiation - Calculus
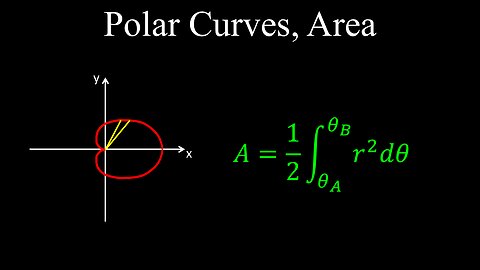
Polar Curve, Area of Region, Integration - Calculus
Polar Curve, Area of Region between Two Curves, Examples - Calculus
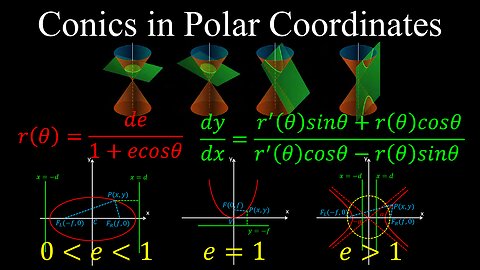
Conics in Polar Coordinates, Derivatives, Example - Calculus
Infinite Sequence, Definition, Representations, Convergence - Calculus
Infinite Series, Definition, Partial Sum, Convergence - Calculus
Geometric Series, Sum, Convergence - Calculus
nth Term Test, Divergence, Infinite Series, Examples - Calculus
Integral Test, Convergence, Infinite Series, Example - Calculus
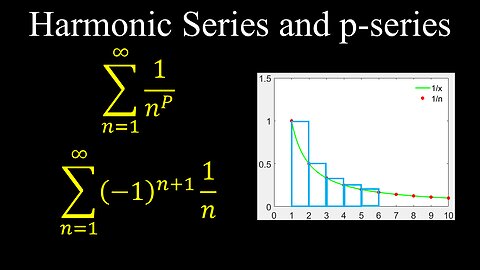
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
Alternating Series Test, Infinite Series - AP Calculus BC
Ratio Test, Infinite Series, Convergence, Examples - Calculus
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
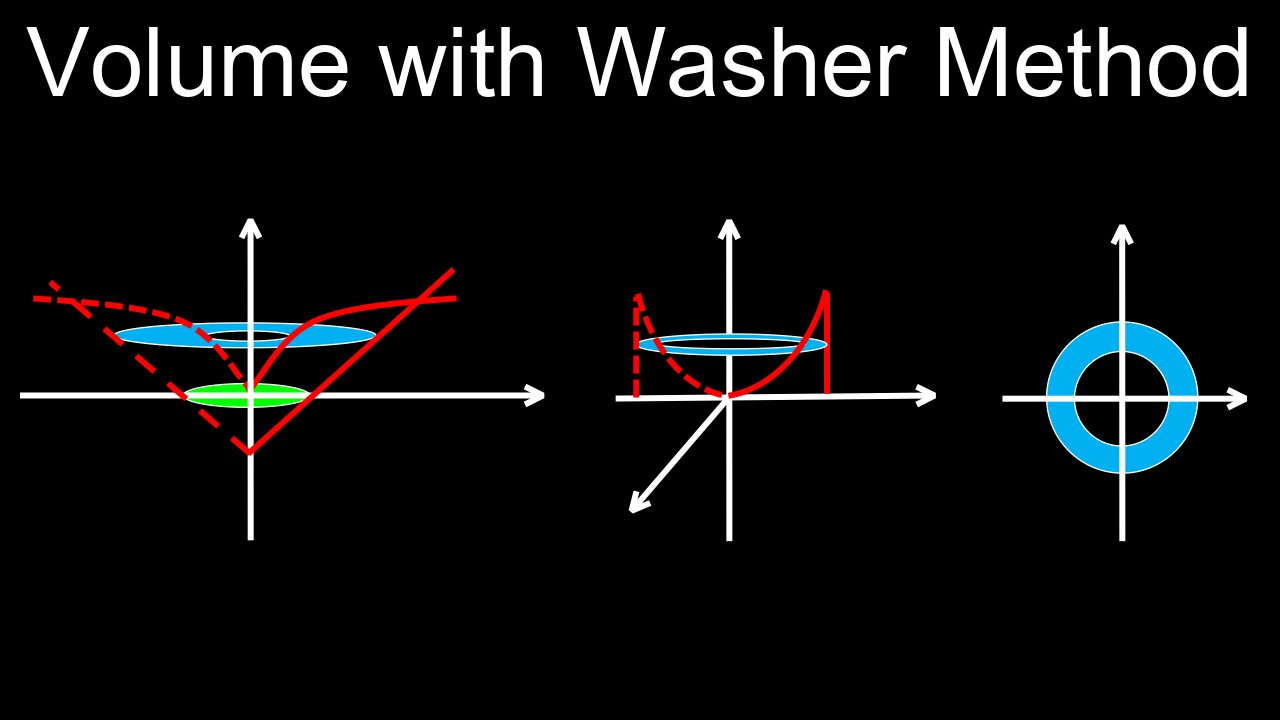
Volume with the Washer Method, Formula, Examples, Practice Problems - Calculus
The washer method calculates the volume of a solid of revolution with a hole by integrating the area of its "washers" (hollow discs). The volume of a single washer is found by subtracting the volume of the inner cylinder from the outer one, which is equivalent to \(\pi (R^{2}-r^{2})\Delta x\), where \(R\) is the outer radius, \(r\) is the inner radius, and \(\Delta x\) is the thickness. To find the total volume, you set up and solve a definite integral using this formula, where the limits of integration are determined by the intersection points of the functions bounding the region.
💡Steps for using the washer method
• Sketch the region: Draw the region between the two functions and identify the axis of rotation.
• Determine the representative rectangle: Draw a small, representative rectangle that is perpendicular to the axis of rotation. This rectangle will form a washer when rotated.
⚬ If the rectangle is vertical (perpendicular to the x-axis), the thickness is \(dx\), and you will integrate with respect to \(x\).
⚬ If the rectangle is horizontal (perpendicular to the y-axis), the thickness is \(dy\), and you will integrate with respect to \(y\).
• Find the inner and outer radii (\(r\) and \(R\)):
⚬ Outer radius (\(R\)): The distance from the axis of rotation to the outer curve of the region.
⚬ Inner radius (\(r\)): The distance from the axis of rotation to the inner curve of the region.
⚬ This can be found by taking the "outer function" minus the "axis of rotation" (for vertical rectangles) or "right function" minus "axis of rotation" (for horizontal rectangles). Be sure both radii are expressed in terms of the same variable you are integrating with respect to.
• Set up the integral:
⚬ The formula for the volume of a single washer is \(dV=\pi (R^{2}-r^{2})dx\) or \(dV=\pi (R^{2}-r^{2})dy\).
⚬ The total volume is the integral of this expression over the appropriate interval: \(V=\int _{a}^{b}\pi (R(x)^{2}-r(x)^{2})dx\) or \(V=\int _{c}^{d}\pi (R(y)^{2}-r(y)^{2})dy\).
• Find the limits of integration: Determine the values of \(x\) or \(y\) where the inner and outer curves intersect to find the lower and upper bounds of your integral.
• Evaluate the integral: Solve the definite integral to find the numerical volume of the solid.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1GQtYzPXeZpvnm7EdpOAPfEyr-VSltAse/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1urkbDfPaDPsymE8T58TZZJHgeUw-P-qx/view?usp=drive_link
💡Chapters:
00:00 Volume with the washer method, revolve around x and y axes, with example
03:55 Washer method, revolve around other axes, with example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 14:01
14:01
Demons Row
12 hours ago $3.64 earnedRobert Patrick EXPOSES the Truth About Motorcycle Clubs and Gangs
16.7K5 -
 26:11
26:11
Athlete & Artist Show
16 hours ago $0.22 earnedWho Will Make Team Canada + Finland IIHF Controversy
2.57K1 -
 3:38
3:38
Blackstone Griddles
16 hours agoBlackstone Betty's Avocado Toast on the Blackstone Griddle
5.02K1 -
 23:17
23:17
Fit'n Fire
20 hours ago $1.88 earnedShould You Own A Budget Rifle? PSA Freedom 15 vs Hi-Point HP15 vs Kel-Tec RDB
3.43K9 -
 8:26
8:26
Hollywood Exposed
15 hours agoKid Rock LEAVES Bill Maher Scrambling After Trump Debate Gets Messy
4.74K9 -
 LIVE
LIVE
BEK TV
2 days agoTrent Loos in the Morning - 11/17/2025
198 watching -
 9:25
9:25
MattMorseTV
16 hours ago $43.03 earnedTrump’s GAMBLE just PAID OFF… BIG TIME.
49.5K98 -
 18:03
18:03
Nikko Ortiz
20 hours agoNikko Ortiz Night Routine...
105K19 -
 LIVE
LIVE
FyrBorne
11 hours ago🔴Battlefield REDSEC Live M&K Gameplay: Pyro+ Games
171 watching -
 LIVE
LIVE
Lofi Girl
3 years agolofi hip hop radio 📚 - beats to relax/study to
387 watching