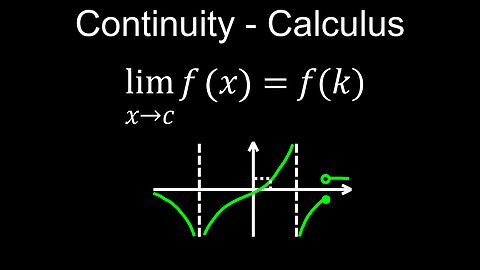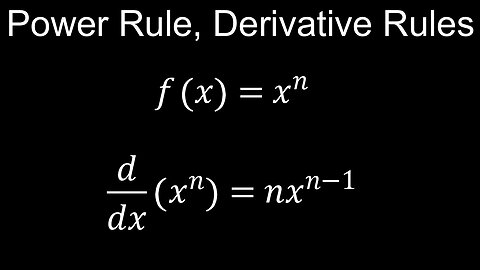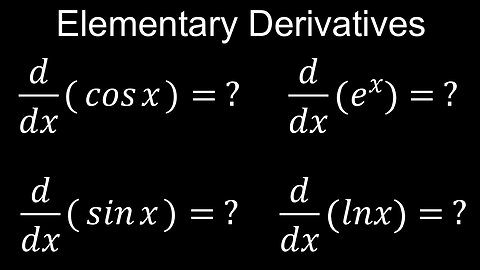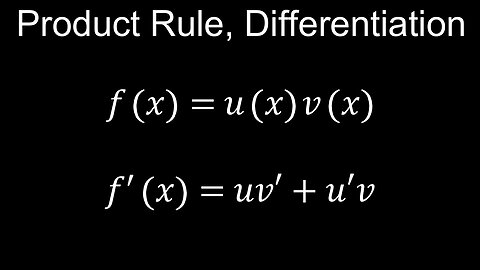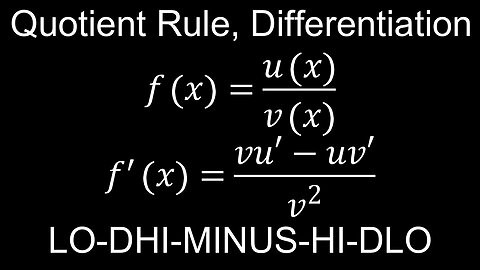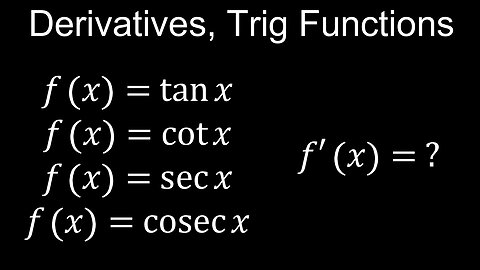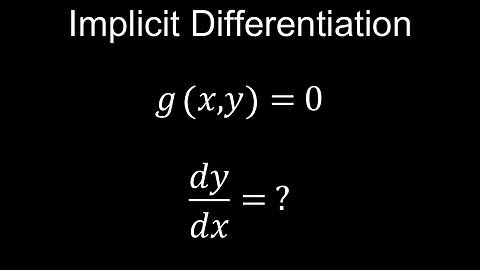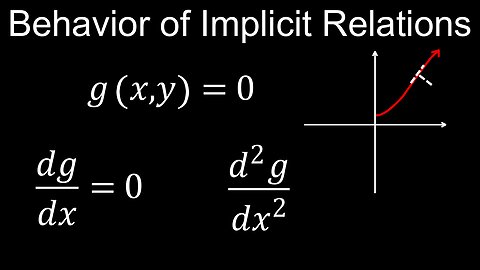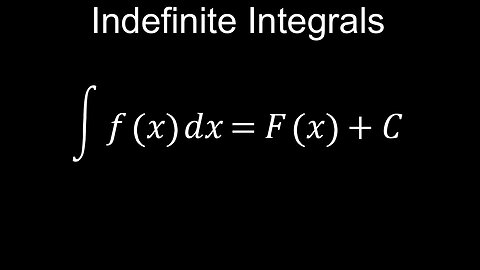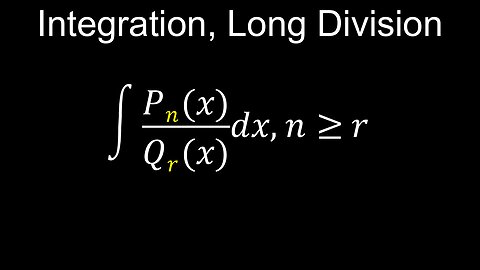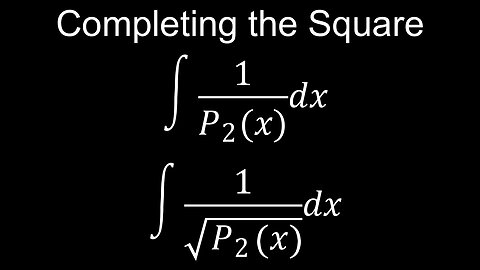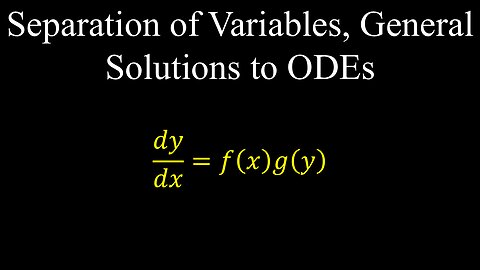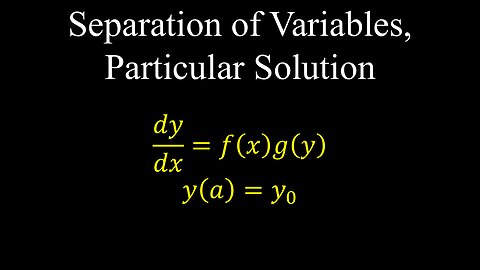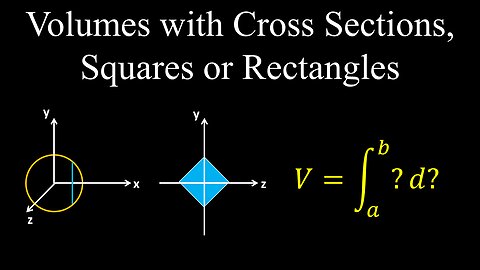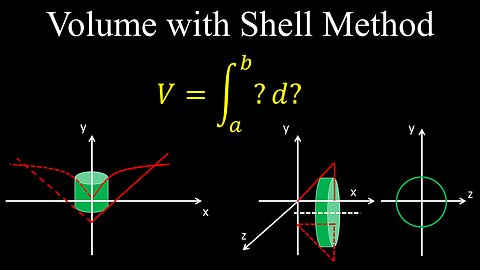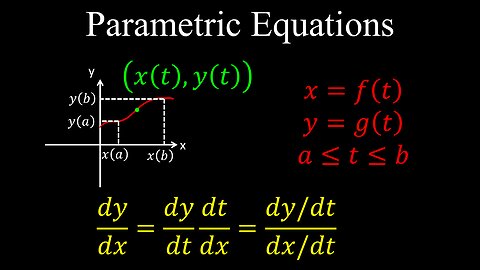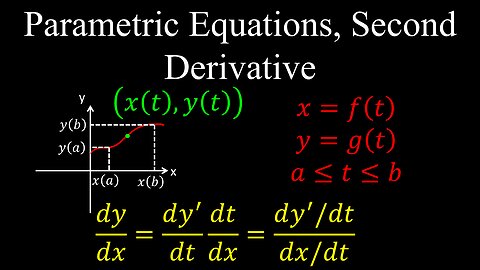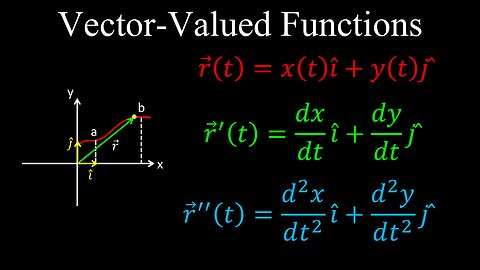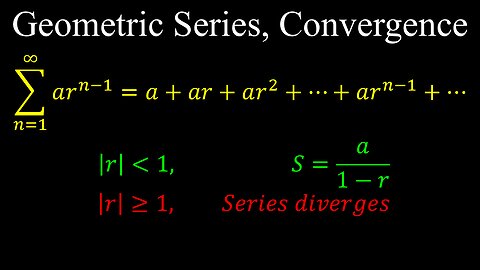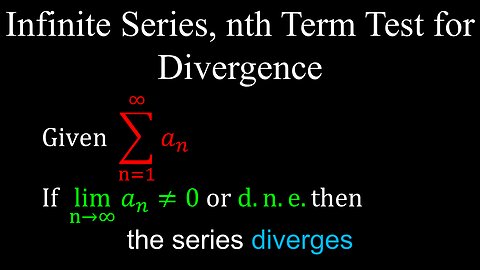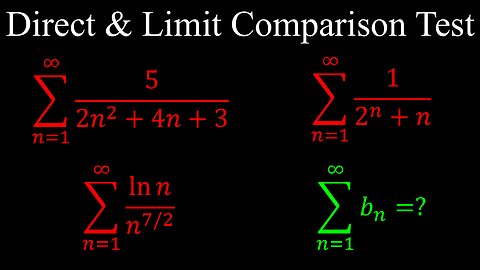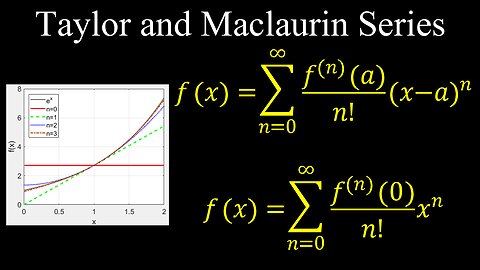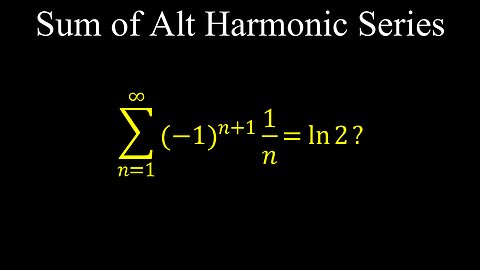Premium Only Content
Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
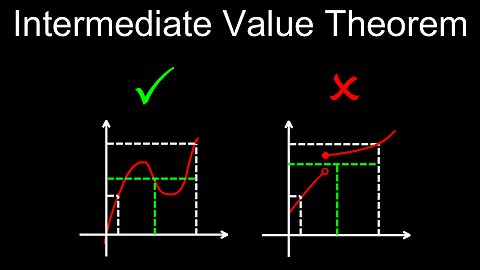
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
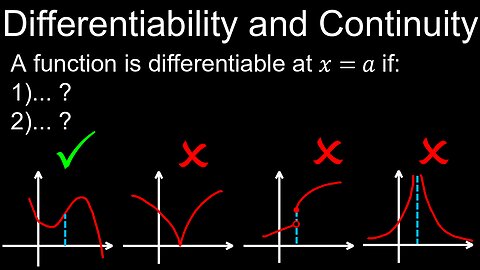
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
Derivative Rules, Power Rule for Differentiation - Calculus
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
Product Rule, Differentiation, Basic Proof, Examples - Calculus
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
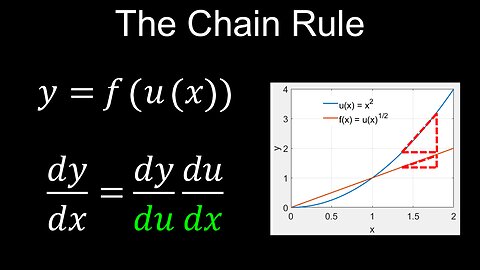
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
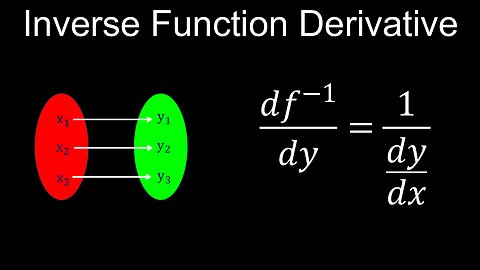
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
Derivatives in Context, Interpretation, Examples - Calculus
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
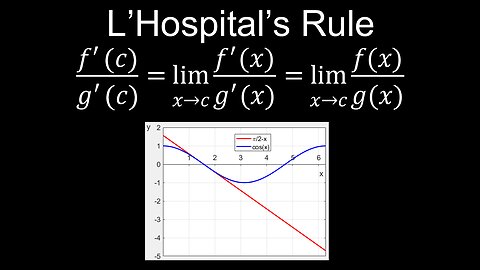
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
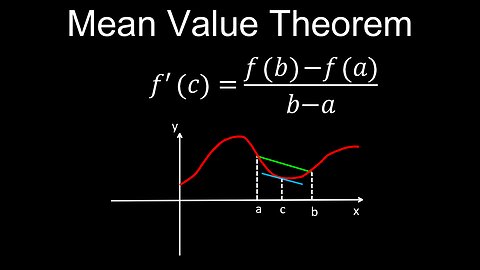
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
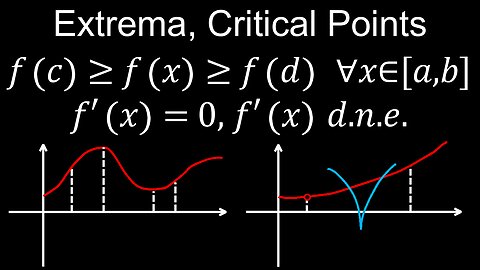
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
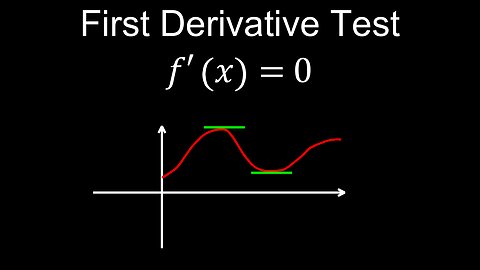
First Derivative Test, Local Extrema, Examples - Calculus
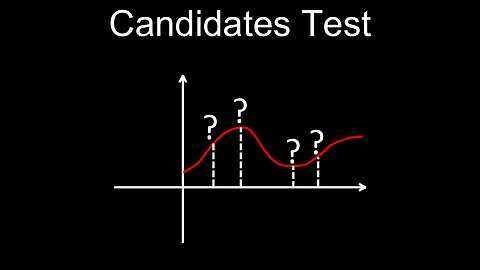
Candidates Test, Global Extrema, Example - Calculus
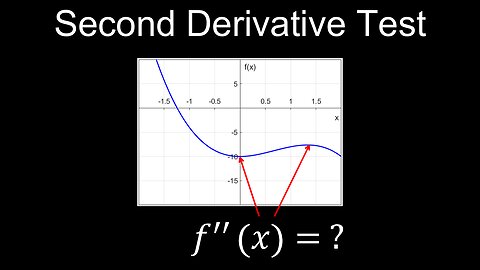
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
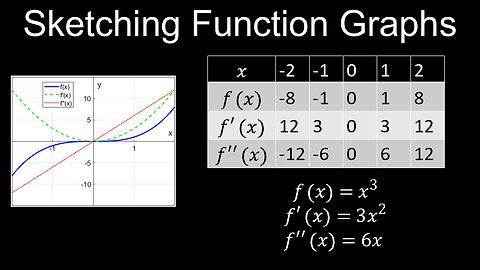
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
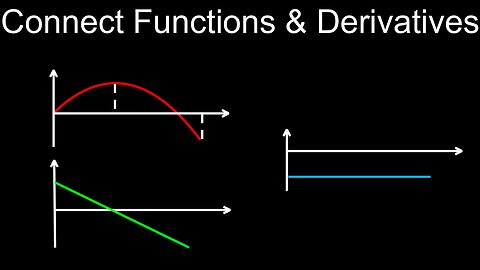
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
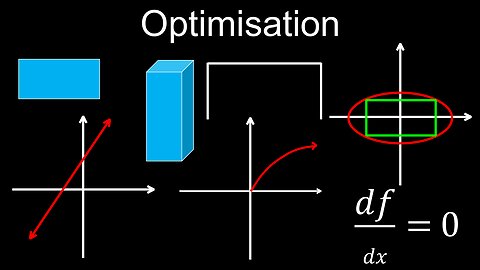
Solving Optimisation Problems, Differentiation, Examples - Calculus
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
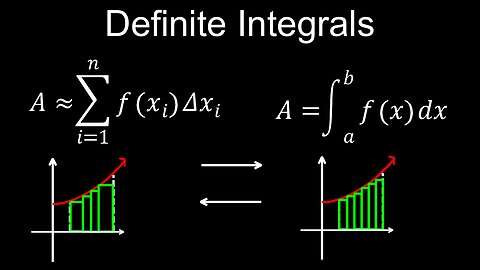
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
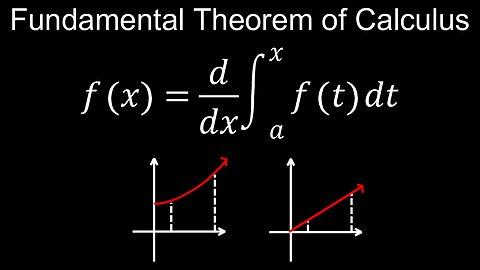
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
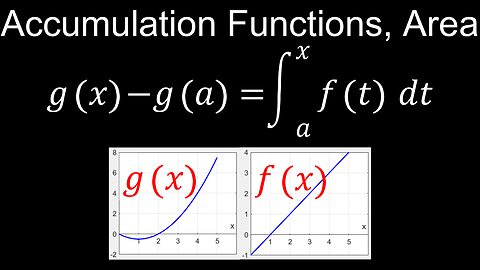
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by Parts, Formula, Rule, Example, Order - Calculus
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
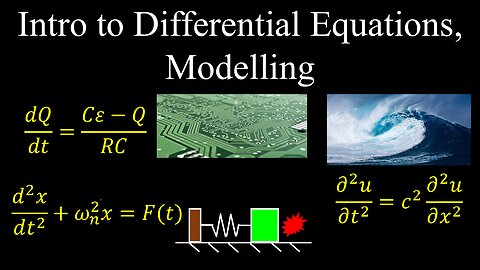
Intro to Differential Equations, Modelling - Calculus
Verifying Solutions to Differential Equations - Calculus
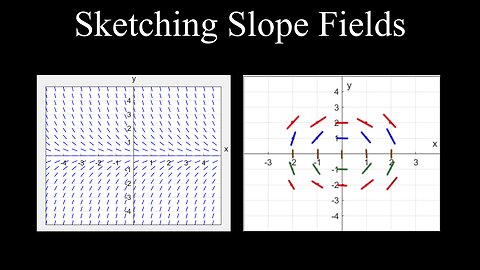
Sketching Slope Fields, Differential Equations - Calculus
Sketching Solution Curves, Slope Fields - Calculus
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
Separation of Variables, General Solution, ODEs - Calculus
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
Exponential Models, Growth, Decay, Differential Equations - Calculus
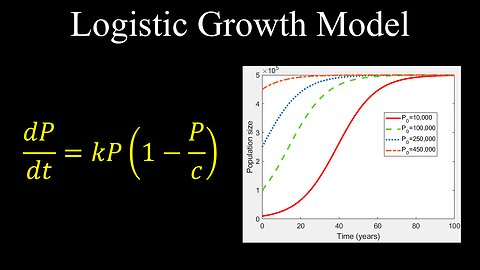
Logistic Growth Model, Differential Equations - Calculus
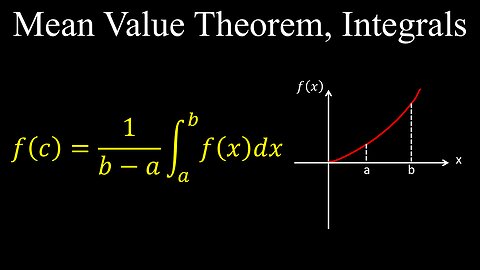
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
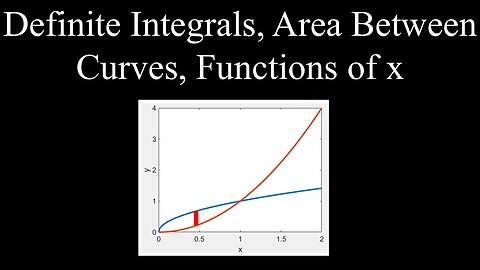
Definite Integrals, Area Between Curves, Functions of x - Calculus
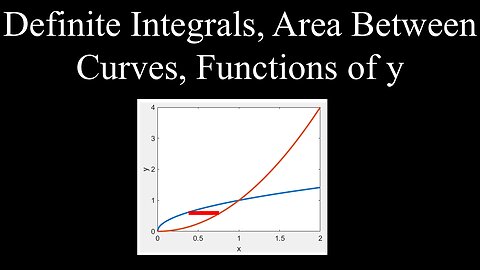
Definite Integrals, Area Between Curves, Functions of y - Calculus
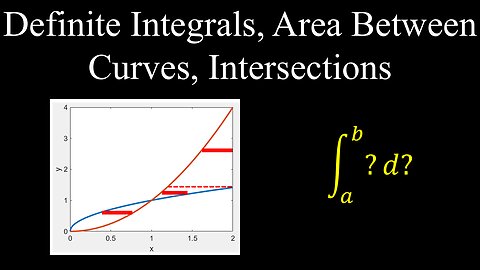
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
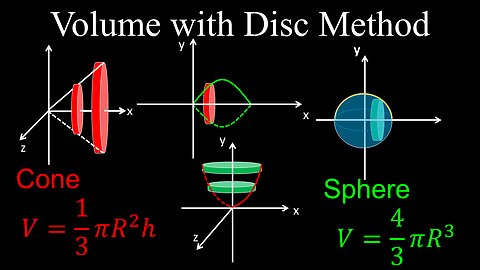
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
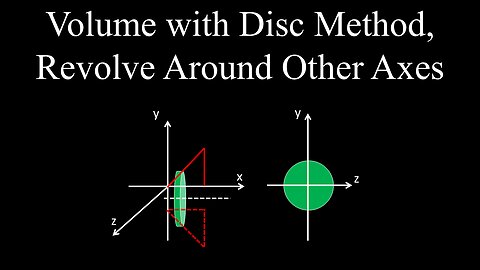
Volume with the Disk Method, Revolving Around other Axes - Calculus
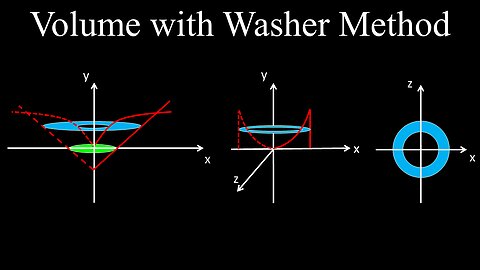
Washer Method to Find the Volume of a Revolved Solid - Calculus
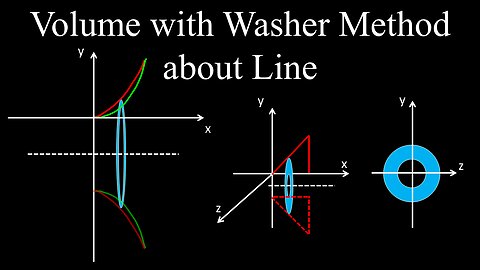
Volume with the Washer Method, Revolved Solid Around Line - Calculus
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
Parametric Equations, Definition, Differentiation - Calculus
Parametric Equations, Second Derivative - Calculus
Parametric Curve, Arc Length, Distance - Calculus
Vector-Valued Functions, Differentiation, Examples - Calculus
Vector-Valued Function, Integration - Calculus
Vector-Valued Functions and Motion in 2D Space - Calculus
Polar Coordinates, Polar Curves, Differentiation - Calculus
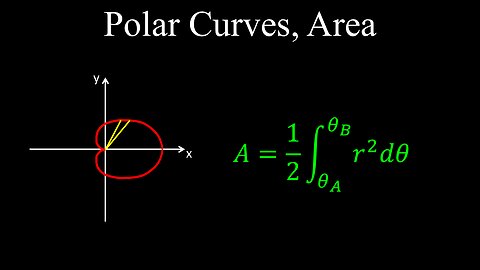
Polar Curve, Area of Region, Integration - Calculus
Polar Curve, Area of Region between Two Curves, Examples - Calculus
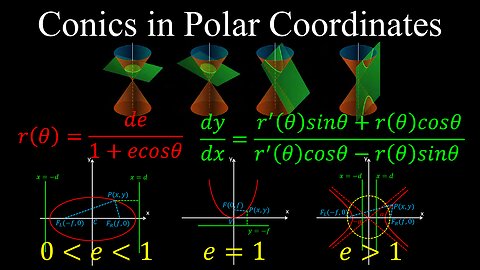
Conics in Polar Coordinates, Derivatives, Example - Calculus
Infinite Sequence, Definition, Representations, Convergence - Calculus
Infinite Series, Definition, Partial Sum, Convergence - Calculus
Geometric Series, Sum, Convergence - Calculus
nth Term Test, Divergence, Infinite Series, Examples - Calculus
Integral Test, Convergence, Infinite Series, Example - Calculus
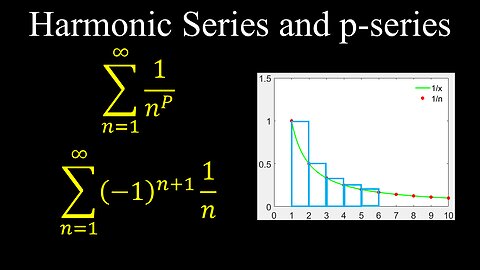
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
Alternating Series Test, Infinite Series - AP Calculus BC
Ratio Test, Infinite Series, Convergence, Examples - Calculus
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
Alternating Series, Error Bound - Calculus
Taylor Polynomials, Approximating Functions - Calculus
Lagrange Error Bound, Taylor Polynomials - Calculus
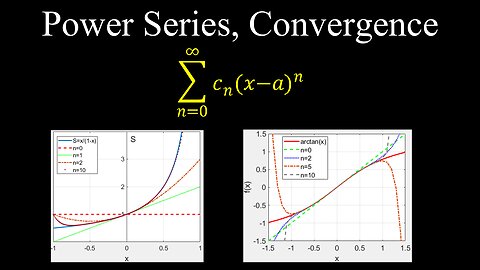
Power Series, Convergence - Calculus
Taylor Series, Maclaurin Series - Calculus
Representing Functions as Power Series - Calculus
Sum of Alternating Harmonic Series (-1)^(n+1)1/n = ln2 - Calculus
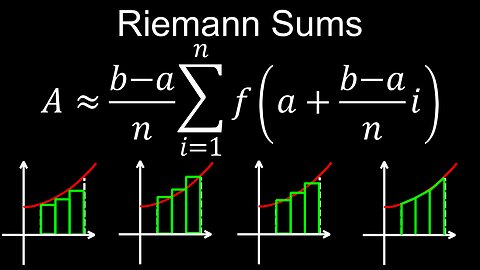
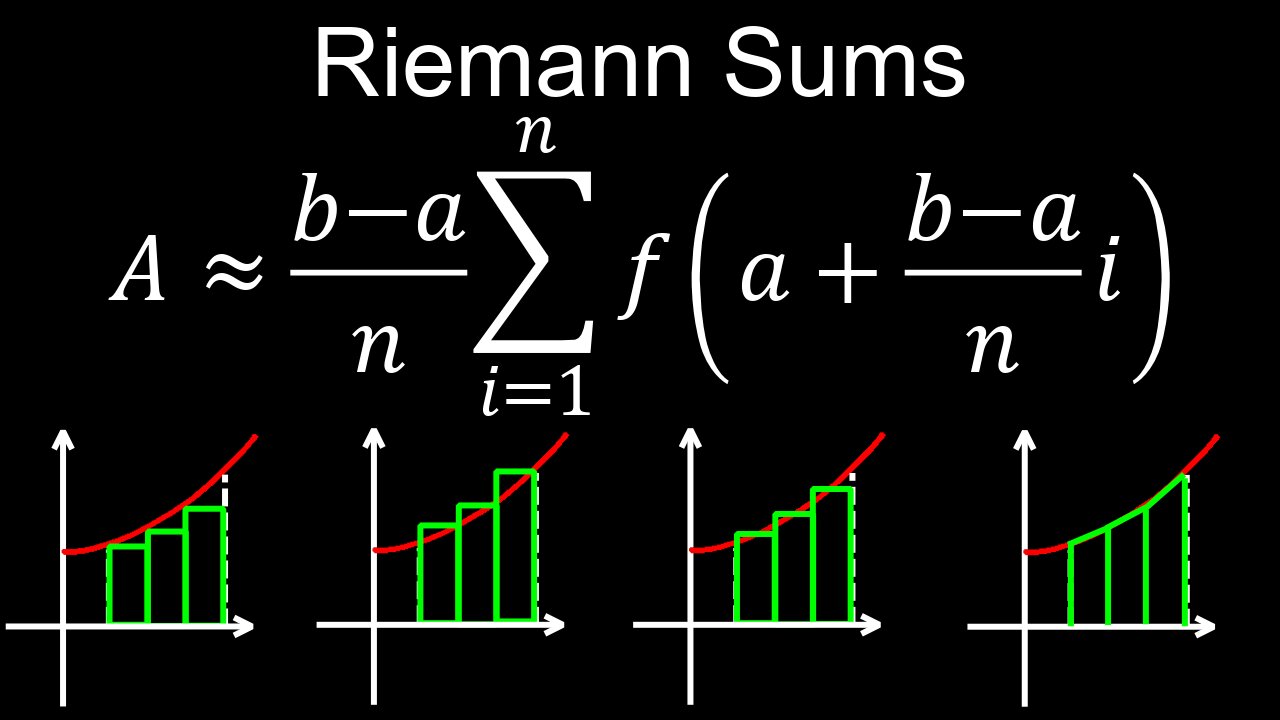
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
A Riemann sum approximates the area under a curve by dividing the region into a series of rectangles and summing their areas. The width of each rectangle is a subinterval, and its height is determined by evaluating the function at a specific point within that subinterval, such as the left endpoint, right endpoint, or midpoint. By increasing the number of rectangles, the Riemann sum becomes a more accurate approximation of the exact area under the curve, which is found by taking the limit as the number of rectangles approaches infinity.
💡How Riemann Sums Work
• Divide the Interval: The interval over which you want to find the area is divided into smaller, equally-sized subintervals.
• Construct Rectangles: For each subinterval, a rectangle is formed with the x-axis as its base.
• Determine Rectangle Height: The height of each rectangle is found by evaluating the function at a chosen point within its subinterval. Common choices include:
◦ Left Endpoint Rule: The height is determined by the function's value at the left-most point of the subinterval.
◦ Right Endpoint Rule: The height is determined by the function's value at the right-most point of the subinterval.
◦ Midpoint Rule: The height is determined by the function's value at the midpoint of the subinterval.
• Calculate Rectangle Area: The area of each individual rectangle is calculated by multiplying its width (the subinterval's width) by its height.
• Sum the Areas: The Riemann sum is the total of the areas of all these rectangles.
💡The Relationship to Integration
• A Riemann sum is an approximation of the definite integral. As the number of rectangles increases, the approximation becomes more precise. When the number of rectangles approaches infinity, the Riemann sum converges to the exact area under the curve, which is the value of the definite integral.
💡Purpose of Riemann Sums
• Approximation: Riemann sums provide a way to estimate the area under a curve when an exact antiderivative might be difficult or impossible to find.
• Foundation of Integration: They serve as a fundamental concept in calculus, illustrating how a continuous function's area can be broken down and added up.
• Building Intuition: By visualizing the process of subdivision, approximation, and summation, Riemann sums help in understanding the underlying principles of integral calculus.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Intro to Riemann sums
01:26 Left Riemann sum
02:42 Right Riemann sum
03:33 Midpoint Riemann sum
04:47 Trapezoidal sum
06:20 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 LIVE
LIVE
Dr Disrespect
5 hours ago🔴LIVE - DR DISRESPECT - ARC RAIDERS - DANGEROUS ADVENTURES (LEVEL 12)
1,406 watching -
 14:15
14:15
Tactical Advisor
5 days agoEverything You Need To Know About PSA Mixtape Vol 1. (FIRST LOOK)
2.82K3 -
 LIVE
LIVE
Jeff Ahern
1 hour agoFriday Freak out with Jeff Ahern
103 watching -
 14:54
14:54
The Kevin Trudeau Show Limitless
2 days agoThe Hidden Force Running Your Life
54.4K8 -
 1:03:55
1:03:55
Sean Unpaved
3 hours agoRavens' Resurrection Night: Lamar Buries Miami, NFL/CFB Spooky HC Shifts, & Kalshi's Week 9/10 Odds!
26.5K -
 2:16:48
2:16:48
Film Threat
1 day agoHALLOWEEN HORROR + BACK TO THE FUTURE RERELEASE + MORE REVIEWS | Film Threat Livecast
16.4K -
 1:21:16
1:21:16
Steven Crowder
6 hours ago10th Annual Halloween Spooktacular: Reacting to the 69 Gayest Horror Movies of All Time
297K168 -
 57:39
57:39
The Rubin Report
5 hours agoKamala Gets Visibly Angry as Her Disaster Interview Ends Her 2028 Election Chances
49.1K61 -
 LIVE
LIVE
LFA TV
18 hours agoLIVE & BREAKING NEWS! | FRIDAY 10/31/25
1,491 watching -
 1:36:11
1:36:11
The Mel K Show
4 hours agoHunters Become the Hunted: A Reckoning Is Finally Coming - 10/31/25
26.3K15