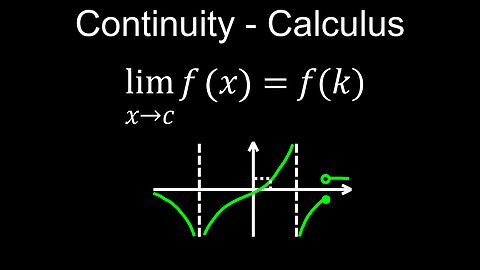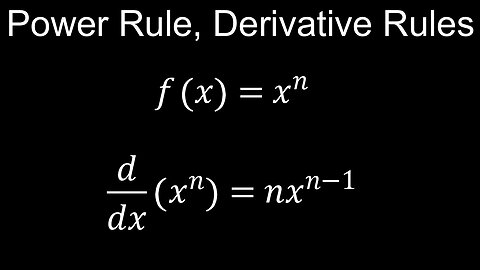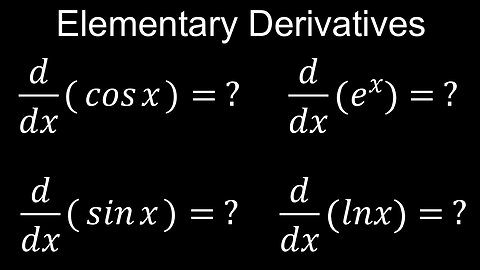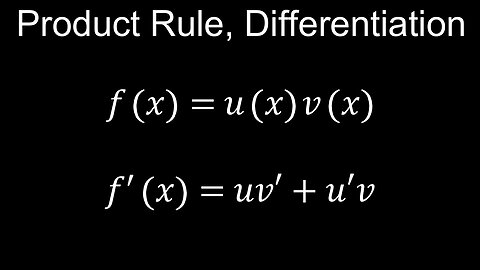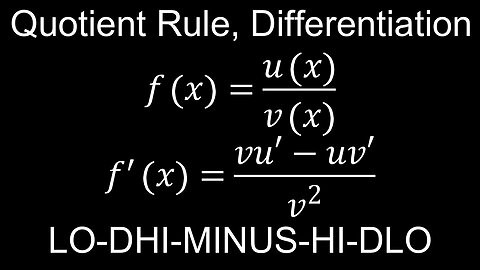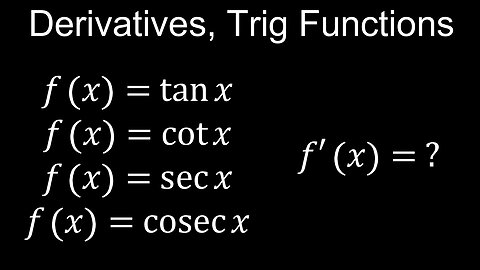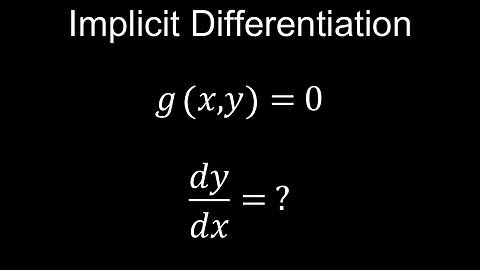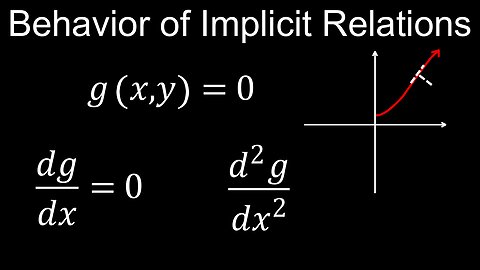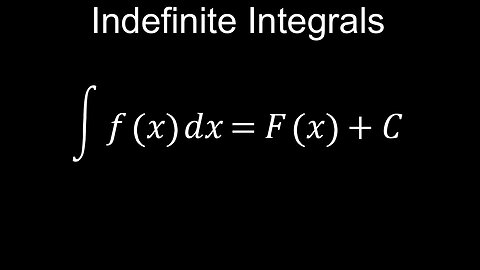Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.
1
Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
DrOfEng
In calculus, a limit describes the behavior of a function as its input approaches a specific value, focusing on what the function gets infinitely close to, rather than its value at the exact point itself. Limits are fundamental because they are used to define continuity, derivatives, and integrals, which are the core concepts of calculus.
💡Key aspects of limits:
• Approaching a value: Limits look at what value a function "approaches" as the input gets closer and closer to a specific number, from both the left and the right sides.
• Not the function's value: The limit doesn't care about the function's actual value at the specific input point; it only cares about the behavior of the function near that point.
• Fundamental to calculus: Limits are the building blocks for understanding continuity, the instantaneous rate of change (derivatives), and the area under a curve (integrals).
💡How limits work:
• One-Sided Approach: To find a limit, you examine the function's behavior as the input approaches the target value from the left (values smaller than the target) and from the right (values larger than the target).
• Existence: A limit only exists if the function approaches the same value from both the left and the right.
• Notation: Limits are represented with the notation: lim f(x): means "the limit of the function f(x)". x → a: means "as x approaches a". For example, lim (x → a) f(x) = L is read as "the limit as x approaches a of f(x) equals L"
💡Why they matter:
• Defining Continuity: A function is continuous at a point if its limit at that point equals the function's actual value there.
• Defining Derivatives: The concept of a limit is used to define the derivative, which measures the instantaneous rate of change of a function.
• Defining Integrals: Limits are also used in the definition of definite integrals, which represent the area under a curve.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1IfdCaeJTszq4Is48tDhUUxlMd-w9Eltx/view?usp=drive_link
• Answers: https://drive.google.com/file/d/11PKq7Z-aEJQOqR_xbqFdAEQdQH4JjKnu/view?usp=drive_link
💡Chapters:
00:00 Why limits? Change at an instant.
01:08 Definition of a limit
01:57 Evaluate limits using graphs
03:27 Evaluate limits numerically using tables
04:39 Algebraic properties of limits
06:11 Evaluating limits using algebra
08:09 Examples on selecting methods for evaluating limits
13:24 Squeeze theorem
17:01 Examples on connecting representations of limits
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://www.youtube.com/channel/UCJAvCW22EeE_2s2ZlJne7uQ?sub_confirmation=1
_______________________
⏩Playlist Link: https://www.youtube.com/playlist?list=PLm_WLG6GdV3vHdHSwImjsL4qzNf_9Qwlh
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://rumble.com/user/DrOfEng
1
comment
2
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
DrOfEng
In calculus, a function is continuous if its graph can be drawn without lifting your pen, meaning there are no breaks or jumps. More formally, a function f(x) is continuous at a point a if three conditions are met: f(a) is defined, the limit of f(x) as x approaches a exists, and the limit equals f(a).
💡Intuitive Understanding
• No Gaps or Jumps: You can draw the graph of a continuous function without your pencil leaving the paper.
• Small Input, Small Output: A small change in the input (x) results in a small change in the output (f(x)).
💡The Formal Definition (at a Point a)
For a function f(x) to be continuous at a point a, all three of the following conditions must be true:
• f(a) is defined: The function must have a specific, defined value at the point a.
• The limit of f(x) as x approaches a exists: The function must approach the same value as x gets closer and closer to a from both the left and right sides.
• The limit equals the function value: The value the function approaches (the limit) must be the same as the actual value of the function at a, i.e., lim x→a f(x) = f(a).
💡Discontinuities
If any of these three conditions are not met, the function is discontinuous at that point. Common types of discontinuities include:
• Removable: A "hole" in the graph that could be "filled".
• Jump: The graph jumps from one value to another, like the function f(x) = {-1 for x less than or equal to 0 and 1 for x greater than 0 at x=0}.
• Infinite: A vertical asymptote where the function's value goes to positive or negative infinity.
💡Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1IfdCaeJTszq4Is48tDhUUxlMd-w9Eltx/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11PKq7Z-aEJQOqR_xbqFdAEQdQH4JjKnu/view?usp=drive_link
💡Chapters:
00:00 Types of discontinuities
01:58 Discontinuities, examples
04:26 Continuity at a point, with examples
08:16 Continuity over an interval, with example
10:55 Removing discontinuities, with example
13:42 Infinite limits and vertical asymptotes
14:41 Infinite limits and horizontal asymptotes
15:34 Relative magnitudes of functions
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
3
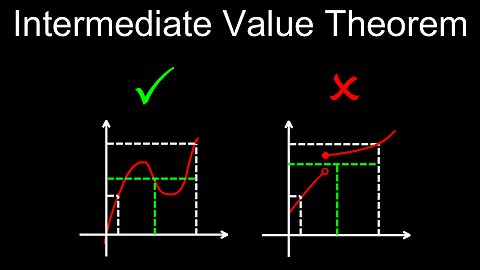
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
DrOfEng
This video explains the Intermediate Value Theorem, including formula, statement, meaning, conditions, application to analysis for determining if a root exists, loose visual proof, walkthrough example exercises and practice problems and solutions (PDF).
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1IfdCaeJTszq4Is48tDhUUxlMd-w9Eltx/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11PKq7Z-aEJQOqR_xbqFdAEQdQH4JjKnu/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Intermediate Value Theorem definition
01:02 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://www.youtube.com/channel/UCJAvCW22EeE_2s2ZlJne7uQ?sub_confirmation=1
What part of Limits and Continuity gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://www.youtube.com/playlist?list=PLm_WLG6GdV3vHdHSwImjsL4qzNf_9Qwlh
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
4
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
DrOfEng
This video explains what the meaning of the derivative is in maths (typically class 11 and 12 calculus), including introduction, formula, definition by first principle, how to represent and estimate it graphically, numerically, analytically, verbally and using technology. Worked example practice problems are provided. You will be able to use the definition to prove the derivatives of elementary functions like sin, cos, tan, ln, e to the power x, ex, x and trigonometric functions.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1PHEth8jm90Yy-42wKfBXG6_-1oi2nUDL/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1wlHR_SPWlSvvi0RjTmYAaxscP6WPTr-l/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Rate of change at a point
01:35 Definition of the derivative, with example
04:09 Representing the derivative
06:21 Derivatives at a point
07:40 Estimate the derivative using technology
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://www.youtube.com/channel/UCJAvCW22EeE_2s2ZlJne7uQ?sub_confirmation=1
What part of Differentiation (Definition and Fundamental Properties) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://www.youtube.com/playlist?list=PLm_WLG6GdV3vHdHSwImjsL4qzNf_9Qwlh
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
5
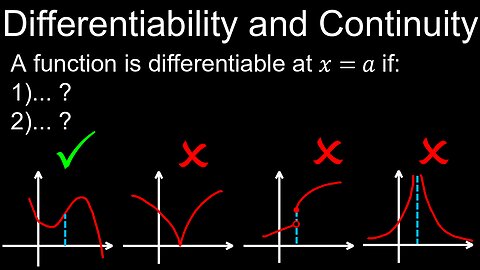
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
DrOfEng
This video explains how differentiability implies continuity (3 conditions) of a function (e.g. composite or complex), including a basic introduction and visual proof using graphs and the limit formula, how to know if a function is differentiable at a point or when a function is not differentiable by first principles, and worked example practice questions. This topic is typically covered in class 11 or 12 maths. Understanding this topic is crucial to the chain, product and quotient rules, evaluating the derivatives of functions like sin, e^x, log and applying other differentiation rules.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-IfxXvhpMp43qxNG-21ZtIPqO4WMuvOk/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1nchFi76DuCzBIx0TWesDVjlUz0qvNG7o/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Differentiability and continuity
02:03 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Definition and Fundamental Properties) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
6
Derivative Rules, Power Rule for Differentiation - Calculus
DrOfEng
This video explains how to apply derivative rules like the power rule in a few minutes, which you can add to your Calculus 1 and 2 cheat sheet and apply to differentiate logarithmic (ln), exponential (e), trigonometric (trig) and other functions. A basic review and proof of the power law formula are given, which is applied in examples (PDF) where the exponents have fractions.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-IfxXvhpMp43qxNG-21ZtIPqO4WMuvOk/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1nchFi76DuCzBIx0TWesDVjlUz0qvNG7o/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Power rule proof, binomial theorem
01:33 Derivative rules
03:17 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://www.youtube.com/channel/UCJAvCW22EeE_2s2ZlJne7uQ?sub_confirmation=1
What part of Differentiation (Definition and Fundamental Properties) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://rumble.com/user/drofeng
7
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
DrOfEng
This video explains how to derive the derivatives of common elementary functions using first principles, which you can add to your Calculus 1 and 2 cheat sheet or formula sheet, including basic logarithmic (ln), exponential (e) and trigonometric (sin and cos). A worksheet (PDF) of worked example practice problems is provided.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-IfxXvhpMp43qxNG-21ZtIPqO4WMuvOk/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1nchFi76DuCzBIx0TWesDVjlUz0qvNG7o/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Derivative of cos(x)
01:24 Derivative of sin(x)
02:50 Derivative of e^x
03:37 Derivative of ln(x)
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Definition and Fundamental Properties) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
8
Product Rule, Differentiation, Basic Proof, Examples - Calculus
DrOfEng
This video explains how to derive the product rule using first principles, which is commonly taught in class 11, 12 or A level maths. It is used extensively in physics and you can add it to your formula sheet or cheat sheet. The other important rules to be covered later are the quotient rule and chain rule. A worksheet (PDF) of worked example practice questions (problems) with solutions is provided, which also shows how the product rule can be applied to functions with three terms.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-IfxXvhpMp43qxNG-21ZtIPqO4WMuvOk/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1nchFi76DuCzBIx0TWesDVjlUz0qvNG7o/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Product rule derivation
01:42 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Definition and Fundamental Properties) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
9
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
DrOfEng
This video explains how to apply the quotient rule formula for differentiating quotients of two functions (like uv, u and v). which is covered in class 11, 12 and A level maths. It can be applied to evaluate the derivatives of quotients of radicals, polynomials, logarithms and so on. The proof is deferred until the chain rule is covered. Worked example practice questions with solutions are provided.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-IfxXvhpMp43qxNG-21ZtIPqO4WMuvOk/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1nchFi76DuCzBIx0TWesDVjlUz0qvNG7o/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Quotient rule, mnemonic
00:38 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Definition and Fundamental Properties) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
10
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
DrOfEng
This video explains how to evaluate the derivatives of trigonometric or circular functions using the product and quotient rules. You can memorise these derivatives and add them to your formula sheet. Trig identities are also applied to simplify the derivatives. Worked examples (PDF) with solutions are provided. The derivatives of inverse trig functions are deferred as they require the chain rule.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-IfxXvhpMp43qxNG-21ZtIPqO4WMuvOk/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1nchFi76DuCzBIx0TWesDVjlUz0qvNG7o/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Derivative of tan(x)
01:05 Derivative of cot(x)
02:17 Derivative of sec(x)
03:34 Derivative of cosec(x)
04:47 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Definition and Fundamental Properties) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
11
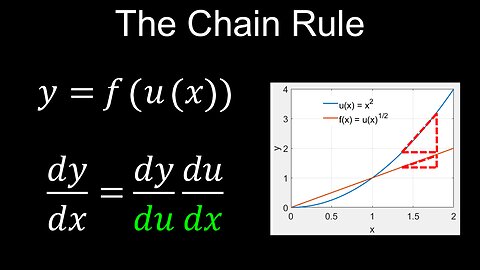
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
DrOfEng
This video explains how to derive (step-by-step basic proof) and apply the chain rule to evaluate the derivatives of composite functions (u v), which is typically covered in class 11 and 12 maths. You can also add this to your formula sheet, along with the product rule and quotient rule. We will use it later to evaluate the derivatives of trig functions, and it can be extended to partial derivatives and integration (u-substitution). Worked example practice questions and solutions are provided to supplement your learning from platforms like Khan Academy.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1Kz_Al0UcyEqyLsrD1taFXvqQps-bHDR4/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11133Xv_5h2foZW0DxqseyDPMIR09aeB3/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Chain rule derivation, composite functions
01:39 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Composite, Implicit and Inverse Functions) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
12
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
DrOfEng
This video explains and reviews the difference between implicit vs explicit functions and what the implicit method of differentiation is, when to use it to find dy/dx using the chain rule, and how to differentiate xy, ln, e, sin and so on. You can remember the method or add it to your formula sheet. Worked example questions or problems (PDF) with solutions are provided for practice. Later on, the applications will be covered, such as finding the equation of the tangent line.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1Kz_Al0UcyEqyLsrD1taFXvqQps-bHDR4/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11133Xv_5h2foZW0DxqseyDPMIR09aeB3/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Implicit differentiation, implicit vs explicit functions
01:15 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Composite, Implicit and Inverse Functions) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
13
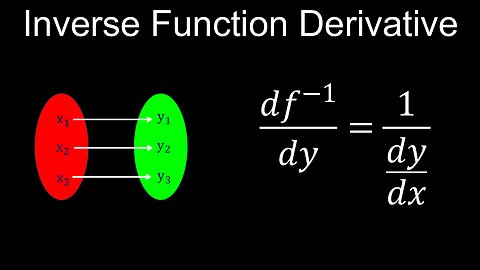
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
DrOfEng
This video explains the differentiation rule or equation and notation for inverse functions (dx dy), where the theorem and formula are commonly taught in class 12 maths. This topic is essential for obtaining inverse trig derivatives. A worksheet (PDF) of example problems is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1Kz_Al0UcyEqyLsrD1taFXvqQps-bHDR4/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11133Xv_5h2foZW0DxqseyDPMIR09aeB3/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Derivatives of inverse functions
01:45 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Composite, Implicit and Inverse Functions) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
14
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
DrOfEng
This video explains the differentiation of inverse trig functions using trig identities, which is commonly taught in class 12 maths. The equations for the derivatives of the inverse of 6 trig functions are summarised and tips are provided on how to remember them. A worksheet (PDF) of example problems is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1Kz_Al0UcyEqyLsrD1taFXvqQps-bHDR4/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11133Xv_5h2foZW0DxqseyDPMIR09aeB3/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Derivatives of inverse trig functions, derivation
01:30 Worked example
02:46 Summary table
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/@drofeng
What part of Differentiation (Composite, Implicit and Inverse Functions) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
15
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
DrOfEng
This video explains how to obtain higher-order derivatives like the second derivative, including definition, formula, implicit differentiation using the chain rule and trigonometric functions. This topic is covered in class 12 maths, engineering maths, bsc 1st year and so on. A worksheet of questions or problems (PDF) and solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1Kz_Al0UcyEqyLsrD1taFXvqQps-bHDR4/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11133Xv_5h2foZW0DxqseyDPMIR09aeB3/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Higher-Order Derivatives
01:10 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Composite, Implicit and Inverse Functions) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
3
comments
16
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
DrOfEng
This video explains how to use some of the 7 rules of logarithms to differentiate logarithmic and exponential functions (e.g. dy/dx for log 4x), as well as the product and chain rules, which are covered in class 12 maths. The formula for simplifying the quotient rule is also covered, and the primary purpose and when to use logarithmic differentiation is made clear. A worksheet (PDF) of questions and answers is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1Kz_Al0UcyEqyLsrD1taFXvqQps-bHDR4/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11133Xv_5h2foZW0DxqseyDPMIR09aeB3/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Logarithmic differentiation
01:08 Differentiating exponential functions
02:07 Quotient rule
03:12 Worked examples
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Differentiation (Composite, Implicit and Inverse Functions) gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
17
Derivatives in Context, Interpretation, Examples - Calculus
DrOfEng
This video explains how to interpret and understand the meaning of the derivative in contextual applications using simple words (what does it mean in context?). This applies to both first and second derivatives. The derivative is essentially the rate of change of one quantity with respect to another. A worksheet (PDF) of questions and answers is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1PHEth8jm90Yy-42wKfBXG6_-1oi2nUDL/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1wlHR_SPWlSvvi0RjTmYAaxscP6WPTr-l/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Derivative in context
01:15 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Contextual Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
18
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
DrOfEng
This video explains how an object's position, velocity and acceleration change over time in one direction or along a single axis (linear motion) using derivatives (rate of change or the slope of the tangent to a graphed curve). This topic is covered in class 11 maths (e.g. AP, NEET, IB) physics and engineering mechanics. Other than connecting position, displacement, velocity and acceleration, which are vector quantities with a magnitude or length and direction, scalar quantities like speed and distance are also covered. You will understand the difference between instantaneous and average quantities using the limit definition formula of the derivative, and when an object is speeding up or slowing down. A worksheet (PDF) of worked example practice problems and answers is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1PHEth8jm90Yy-42wKfBXG6_-1oi2nUDL/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1wlHR_SPWlSvvi0RjTmYAaxscP6WPTr-l/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Displacement vs distance
02:32 Velocity and speed
04:21 Acceleration
05:59 Connecting position, velocity and acceleration
07:24 Worked examples
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Contextual Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
19
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
DrOfEng
This video explains how to solve related rates of change worded problems using the chain rule of differentiation, which is covered in class 12 maths (AP, IB, NEET). Related rates are hard because each problem has a different approach but this tutorial will help you learn to calculate them easily. The problems covered in the video and worksheet involve a cone, cylinder, ladder, area and volume. The worksheet (PDF) includes practice questions and solutions for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1PHEth8jm90Yy-42wKfBXG6_-1oi2nUDL/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1wlHR_SPWlSvvi0RjTmYAaxscP6WPTr-l/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Introduction to related rates
01:47 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Contextual Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
20
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
DrOfEng
This video explains how the local linearisation formula of a differentiable function simplifies calculations by estimating change, which is typically covered in class 12 maths (AP, IB, NEET). The definition, meaning and importance of the method is closely related to zooming in on the tangent line for estimating the value of the function near the given point. The tutorial also demonstrates how the differential method is used for error approximation. You will be able to understand if the error is overestimated or underestimated. A worksheet of problems with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1PHEth8jm90Yy-42wKfBXG6_-1oi2nUDL/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1wlHR_SPWlSvvi0RjTmYAaxscP6WPTr-l/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Local linearity
01:16 Error approximation
02:27 Worked examples
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Contextual Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
21
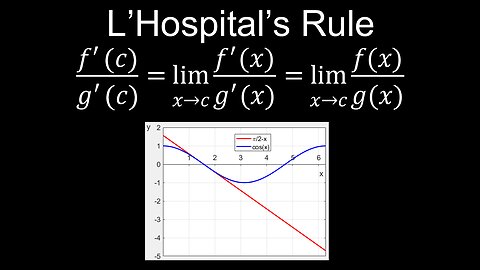
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
DrOfEng
This video explains L'Hôpital's rule in simple terms, which is a method used to evaluate the limits of rational functions that may result in an indeterminate form (0/0 or infinity/infinity), including formula, proof, pronunciation, why it works and when you cannot apply it. L'Hospital's rule is covered class 11 and 12 maths, and engineering mathematics. The basic steps to apply L'Hopital's rule are to check for indeterminacy, find the derivatives, new quotient, evaluate the new limit, and repeat as necessary. A worksheet (PDF) of questions with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1PHEth8jm90Yy-42wKfBXG6_-1oi2nUDL/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1wlHR_SPWlSvvi0RjTmYAaxscP6WPTr-l/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 L'Hopital's rule, proof for indeterminate form 0/0
02:21 L'Hospital's rule, proof for indeterminate form infinity/infinity
06:03 Worked examples
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Contextual Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
22
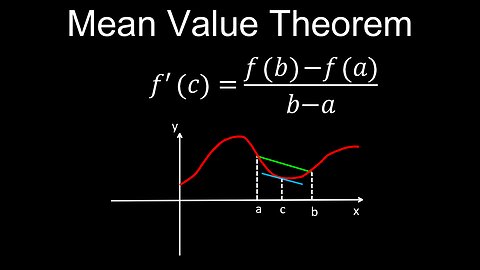
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
DrOfEng
This video explains what is the mean value theorem MVT for differentiation and how it is used in calculus. The MVT formula is covered in class 12 and engineering mathematics and helps with understanding derivatives. Continuity and differentiability are the that need to be satisfied for application of the MVT to first order and higher order derivatives. A worksheet (PDF) of questions with solutions is provided for practice, which includes applications to instantaneous and average velocity and second order derivatives.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 MVT definition and visual proof
01:01 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://www.youtube.com/channel/UCJAvCW22EeE_2s2ZlJne7uQ?sub_confirmation=1
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://rumble.com/user/drofeng
23
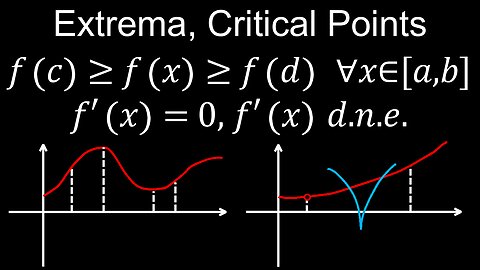
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
DrOfEng
This video explains the extreme value theorem for finding global (absolute) extrema and critical points (local or relative extrema) of functions on a closed interval, which are covered in basic calculus (calc 1, engineering mathematics). You will understand the meaning and why the topic is important through the conditions for extreme values in the definition and example graphs. The first and second derivative test will be covered later on, from which you will be able to distinguish critical points from inflection points. A worksheet (PDF) of problems with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Extreme value theorem
01:11 Critical points
02:09 Global and local extrema
03:17 Worked examples
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
24
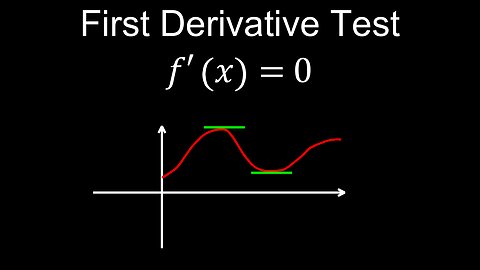
First Derivative Test, Local Extrema, Examples - Calculus
DrOfEng
This video explains the steps and gives the definition of the first derivative test for local maxima and minima, local extreme values of functions or relative extrema. A positive or negative first derivative tells us if a function is increasing/decreasing and identifies critical points. 1st, 2nd and 3rd derivatives of functions like trigonometric ones are calculated in a similar way and a table is typically used for common derivatives. The second derivative test will be covered later on. A worksheet (PDF) of problems with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Determine if a function is increasing/decreasing using the first derivative
01:11 Critical points
01:24 First derivative test
02:38 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
25
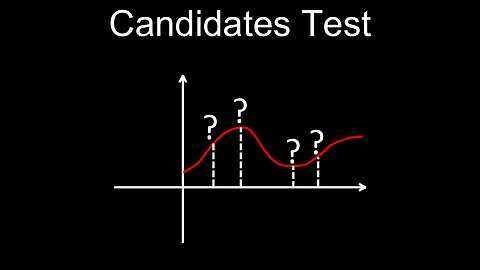
Candidates Test, Global Extrema, Example - Calculus
DrOfEng
This video explains what is the candidates test for absolute extrema, which is covered in class 12 calculus (ap calc ab, bc). It is method for finding the absolute maximum and minimum values (absolute extrema) of a continuous function on a closed interval. You will understand the definition, steps and when to use it vs the first derivative. A worksheet (PDF) of questions with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Determine if a function is increasing/decreasing using the first derivative
01:11 Critical points
01:24 First derivative test
02:38 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
26
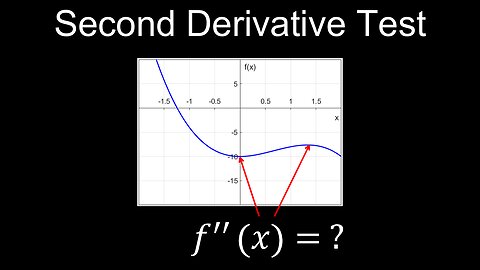
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
DrOfEng
This video explains the second derivative test, which determines if a critical point of a function is a local minimum or maximum (concavity), or inflection point (= 0). The topic is covered in class 12 maths. A worksheet (PDF) of questions with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Concavity of functions
01:17 Second derivative test
02:17 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
27
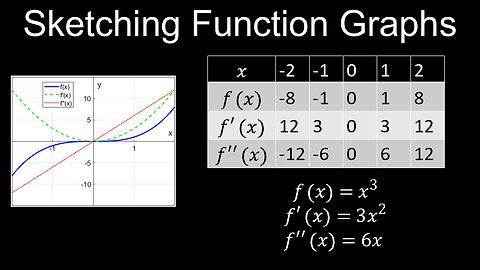
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
DrOfEng
This video explains how to sketch the graphs of original functions using relationships to their derivatives and limits. You will understand the method for matching and connecting the graphs using equations and tables. A worksheet (PDF) of questions with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Graphs of functions
01:28 Worked examples on sketching graphs
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
28
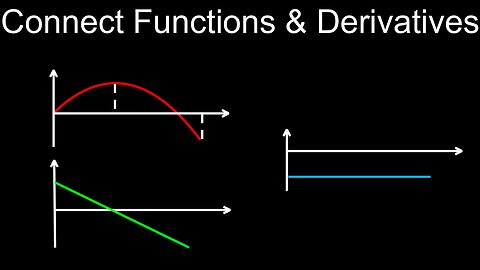
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
DrOfEng
This video explains how to connect functions to their first and second derivative graphs by analysing the slope of the tangent to the curve of the original function. A worksheet (PDF) of questions with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Connecting functions and their first and second derivatives
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
29
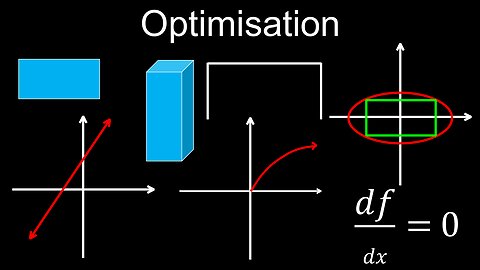
Solving Optimisation Problems, Differentiation, Examples - Calculus
DrOfEng
This video explains how optimisation is used to find the minimum or maximum values of a function (e.g. quadratic), which is used in real-life applications like minimising cost or maximising area. It is typically covered in grade 12 maths (calc 1, ap). The key steps are to reduce the problem to a function of one variable and find a critical point using differentiation. A worksheet (PDF) of questions with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Intro to optimisation
01:56 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
30
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
DrOfEng
This video explains how to analyse the behaviour of implicit functions using implicit differentiation to find the derivatives (dy/dx and y''(x)). Like explicit functions, the derivatives reveal certain properties like increasing/decreasing, horizontal and vertical tangents, critical points and extrema. A worksheet (PDF) of questions with solutions is provided for practice.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 Behaviour of implicit relations
01:54 Worked examples
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://rumble.com/user/drofeng
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
31
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
DrOfEng
"Accumulation of change" is a fundamental calculus concept referring to the total change of a quantity over a specific interval, calculated by integrating its rate of change. For example, if you have the velocity of a car (the rate of change of position), the accumulated change in position (the total distance traveled or displacement) is found by integrating the velocity function over a given time period. This concept is represented graphically as the area under the curve of the rate function within the specified interval.
💡Key Aspects
• Rate of Change: Accumulation of change works with the rate at which a quantity changes.
• Integration: The mathematical operation used to find the accumulation of change is definite integration.
• Net Change: The result is the total, or net, change in the quantity over the interval.
• Graphical Representation: The definite integral of a rate function is equivalent to the area between the curve of that function and the x-axis over a specific interval.
💡Real-World Examples
• Distance Traveled: Integrating a car's velocity over time gives the total distance it has traveled.
• Water in a Tank: Integrating the rate of water flow into a tank gives the total volume of water accumulated over a period.
• Revenue Earned: Integrating the rate of daily earnings gives the total revenue over a week.
💡Distinction from Total Value
• The accumulation of change tells you how much a quantity has changed, but not its total value.
• To find the total value, you need a boundary value—the starting or ending value of the quantity at a specific point. You then add this boundary value to the accumulated change. For instance, if you know the initial amount of water in a tank and add the total water accumulated (from integration) to it, you get the final volume of water.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Accumulation of change from the rate function
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
32
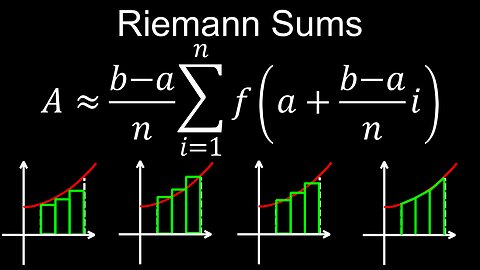
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
DrOfEng
A Riemann sum approximates the area under a curve by dividing the region into a series of rectangles and summing their areas. The width of each rectangle is a subinterval, and its height is determined by evaluating the function at a specific point within that subinterval, such as the left endpoint, right endpoint, or midpoint. By increasing the number of rectangles, the Riemann sum becomes a more accurate approximation of the exact area under the curve, which is found by taking the limit as the number of rectangles approaches infinity.
💡How Riemann Sums Work
• Divide the Interval: The interval over which you want to find the area is divided into smaller, equally-sized subintervals.
• Construct Rectangles: For each subinterval, a rectangle is formed with the x-axis as its base.
• Determine Rectangle Height: The height of each rectangle is found by evaluating the function at a chosen point within its subinterval. Common choices include:
◦ Left Endpoint Rule: The height is determined by the function's value at the left-most point of the subinterval.
◦ Right Endpoint Rule: The height is determined by the function's value at the right-most point of the subinterval.
◦ Midpoint Rule: The height is determined by the function's value at the midpoint of the subinterval.
• Calculate Rectangle Area: The area of each individual rectangle is calculated by multiplying its width (the subinterval's width) by its height.
• Sum the Areas: The Riemann sum is the total of the areas of all these rectangles.
💡The Relationship to Integration
• A Riemann sum is an approximation of the definite integral. As the number of rectangles increases, the approximation becomes more precise. When the number of rectangles approaches infinity, the Riemann sum converges to the exact area under the curve, which is the value of the definite integral.
💡Purpose of Riemann Sums
• Approximation: Riemann sums provide a way to estimate the area under a curve when an exact antiderivative might be difficult or impossible to find.
• Foundation of Integration: They serve as a fundamental concept in calculus, illustrating how a continuous function's area can be broken down and added up.
• Building Intuition: By visualizing the process of subdivision, approximation, and summation, Riemann sums help in understanding the underlying principles of integral calculus.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Intro to Riemann sums
01:26 Left Riemann sum
02:42 Right Riemann sum
03:33 Midpoint Riemann sum
04:47 Trapezoidal sum
06:20 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
33
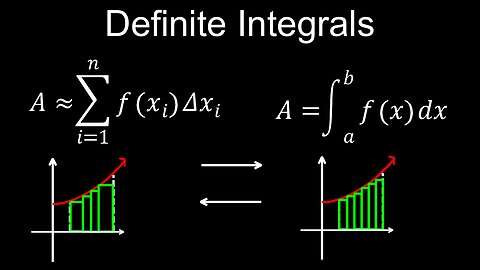
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
DrOfEng
A definite integral calculates the net signed area between a function's curve and the x-axis over a specific interval, defined by a lower limit (a) and an upper limit (b) of integration. The definite integral of a function f(x) from a to b, written as ∫ᵇₐ f(x) dx, is found by calculating the antiderivative F(x) of f(x) and then evaluating F(b) - F(a). The result is a single number representing the exact area, which can be positive, negative, or zero depending on whether the area is above, below, or crosses the x-axis.
💡Key Components and Notation
• Integral Symbol (∫): Indicates the operation of integration.
• Integrand (f(x)): The function being integrated.
• Limits of Integration (a and b): The lower (a) and upper (b) bounds of the interval over which the area is calculated.
• Differential (dx): Indicates the variable of integration.
💡How to Evaluate a Definite Integral
• Find the Antiderivative: Determine the indefinite integral (antiderivative) F(x) of the function f(x).
• Substitute Limits: Substitute the upper limit (b) and the lower limit (a) into the antiderivative F(x).
• Subtract: Subtract the result from the lower limit substitution from the result of the upper limit substitution: F(b) - F(a).
💡Example
To find the definite integral of 2x from 1 to 2:
• Antiderivative: The antiderivative of 2x is x².
• Evaluate at Limits:
◦ Upper limit: (2)² = 4
◦ Lower limit: (1)² = 1
• Subtract: 4 - 1 = 3.
• Therefore, ∫²₁ 2x dx = 3.
💡When and Why to Use Definite Integrals
Definite integrals are used to:
• Calculate Exact Areas: Find the precise area under a curve over a given interval.
• Measure Net Signed Area: Determine the total area above the x-axis minus the total area below the x-axis within the interval.
• Model Accumulation: Measure the total buildup of a quantity over a period when its rate of change is known, such as the total distance traveled by a car given its velocity function over time.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Definite integral, definition
01:38 Integral to Riemann sum
03:33 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
2
comments
34
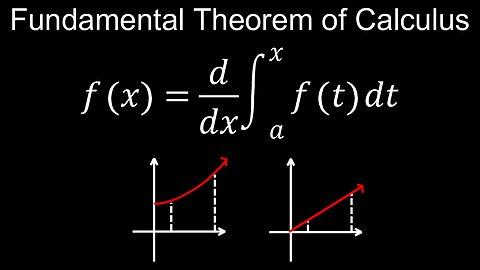
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
DrOfEng
The Fundamental Theorem of Calculus, Part 1, states that if a function f is continuous on an interval [a, b], then the function G(x) defined by the integral of f(t) from a to x (G(x) = ∫_a^x f(t)dt) is continuous on [a, b], differentiable on (a, b), and its derivative, G'(x), is equal to f(x). Essentially, taking the derivative of this integral "undoes" the integration, resulting in the original function f.
💡Key Aspects
• Inverse Operations: This part of the theorem demonstrates that differentiation and integration are inverse operations.
• Antiderivative: The integral G(x) defined in this way is an antiderivative of f(x).
• Conditions: The theorem requires the function f to be continuous on the specified interval.
• The Integral as a Function: The definite integral of f(t) from a constant a to a variable x results in a new function G(x), not just a single numerical value.
💡In simpler terms:
If you define a function G(x) by finding the area under the curve of another function f(t) from a fixed point a up to a variable point x, then the rate at which that area changes (the derivative of G(x)) is simply the height of the curve f(x) at that point x.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Fundamental theorem of calculus, part 1, visual proof
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
35
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
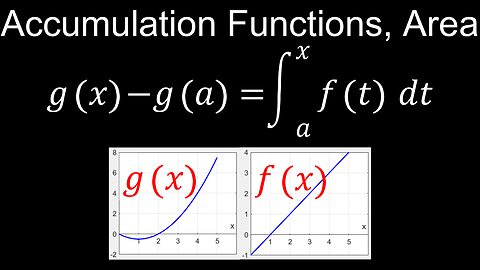
DrOfEng
Accumulation functions represent the running total, or the cumulative area, under the graph of another function, often over a fixed interval starting at a constant point 'a' and extending to a variable point 'x'. For a given function f(t), the accumulation function F(x) = ∫[from a to x] f(t) dt measures this total accumulated quantity, such as distance traveled or total rainfall. The First Fundamental Theorem of Calculus shows that the accumulation function F(x) is an antiderivative of f(x), meaning its rate of change, F'(x), is equal to the original function f(x).
💡Key Characteristics
• Definition: An accumulation function F(x) is defined as a definite integral where the upper limit is a variable, such as F(x) = ∫[from a to x] f(t) dt.
• Meaning: It provides a cumulative measure of the quantity represented by f(t) over the interval from 'a' to 'x'.
• Relationship to the Original Function: According to the First Fundamental Theorem of Calculus, the derivative of an accumulation function F(x) is the original function f(x).
• Behavior:
◦ F(x) increases when f(x) is positive.
◦ F(x) decreases when f(x) is negative.
◦ F(x) has a maximum or minimum value when f(x) = 0, representing points where the area accumulation changes direction.
• Applications: Accumulation functions are used to model quantities that change over time or intervals, such as:
◦ Total distance traveled by a car.
◦ Total amount of water in a tank after a certain time.
◦ Total rainfall over a given period.
💡Example
Consider the function f(t) = 2t representing the velocity of an object at time t. The accumulation function for distance, D(x), would be:
D(x) = ∫[from 0 to x] 2t dt This function D(x) gives the total distance the object has traveled from time 0 to time x, and D'(x) = 2x, which is the original velocity function.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Fundamental theorem of calculus, part 1, visual proof
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
36
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
DrOfEng
Definite integral properties in calculus simplify evaluating integrals and calculating the net signed area under a curve. Key properties include: the integral is zero when limits are the same (\int_a^a f(x)dx = 0), reversing limits changes the sign (\int_a^b f(x)dx = -\int_b^a f(x)dx), an integral of a sum is the sum of integrals (\int_a^b [f(x) \pm g(x)]dx = \int_a^b f(x)dx \pm \int_a^b g(x)dx), a constant factor can be pulled out (\int_a^b kf(x)dx = k\int_a^b f(x)dx), and an integral can be split into two intervals (\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx).
💡Basic Properties
• Zero Integral: If the upper and lower limits of integration are the same, the definite integral is zero.
◦ Formula: \int_a^a f(x)dx = 0
◦ Explanation: The interval has no width, and thus no area is enclosed.
• Reverse Limits: If you swap the upper and lower limits of integration, the sign of the definite integral reverses.
◦ Formula: \int_a^b f(x)dx = -\int_b^a f(x)dx
◦ Explanation: This signifies a change in the accumulated area's direction.
💡Properties for Calculation
• Sum/Difference of Functions: The integral of a sum or difference of functions is the sum or difference of their individual integrals.
◦ Formula: \int_a^b [f(x) \pm g(x)]dx = \int_a^b f(x)dx \pm \int_a^b g(x)dx
◦ Explanation: This property allows you to break down complex integrals into simpler ones.
• Constant Multiple: A constant factor multiplied by a function within an integral can be factored out.
◦ Formula: \int_a^b kf(x)dx = k\int_a^b f(x)dx (where 'k' is a constant)
◦ Explanation: Constants can be pulled out of the integral to simplify the integration process.
• Additive Interval Property: An integral over an interval can be split into the sum of two integrals over sub-intervals.
◦ Formula: \int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx
◦ Explanation: This property is valid for any value of 'c', not just when it lies between 'a' and 'b'.
💡Other Useful Properties
• Variable Substitution: A definite integral's value is independent of the variable of integration.
◦ Formula: \int_a^b f(x)dx = \int_a^b f(t)dt
◦ Explanation: You can replace the variable of integration with another variable, like 't', without changing the outcome.
• Integration of Even and Odd Functions: Properties exist for integrating even or odd functions over symmetric intervals around the origin, which can simplify calculations.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Definite integrals, properties
01:35 Integrals over discontinuities
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
37
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
DrOfEng
The Second Fundamental Theorem of Calculus states that for a continuous function f on the interval [a, b], the definite integral from a to b is equal to the difference between the value of any antiderivative F at b and the value of F at a. Its formula is: ∫baf(x)dx = F(b) − F(a), where F'(x) = f(x). This theorem provides a powerful method for evaluating definite integrals by finding an antiderivative and evaluating it at the integral's limits.
💡Here's a breakdown of the theorem:
• The Setup: You start with a function f(x) that is continuous on the interval [a, b].
• The Antiderivative: You find an antiderivative of f(x), which is any function F(x) such that its derivative, F'(x), is equal to f(x).
• The Calculation: The theorem says that the definite integral, which represents the area under the curve of f(x) from a to b, can be calculated by taking the antiderivative F(x), evaluating it at the upper limit b (F(b)), and then subtracting the value of the antiderivative evaluated at the lower limit a (F(a)).
💡Why is it important?
• Simplifies Calculation: It provides a direct method to calculate definite integrals, replacing the more complex process of breaking the area into infinite tiny rectangles (numerical integration).
• Connects Integration and Differentiation: It establishes a fundamental link between the process of integration and differentiation by showing that integrating a function's derivative gives you back the original function (up to a constant difference).
• Applications: It is widely used in various fields to find total changes by integrating a rate of change. For example, if f(x) is a velocity function, the integral of f(x) from a to b gives the total displacement over that time interval.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Fundamental theorem of calculus, part 2
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
38
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
DrOfEng
An indefinite integral, also known as an antiderivative, is a function whose derivative is the original function. It represents a family of functions that differ by a constant, which is included as a "+ C" in the final result, denoted by the integral symbol (∫) followed by the function and a differential (like dx). For example, the indefinite integral of f(x) is F(x) + C, where F'(x) = f(x).
💡Key Characteristics
• Antiderivative: It is the inverse operation of differentiation.
• Constant of Integration (+ C): This constant is crucial because the derivative of any constant is zero.
• No Fixed Boundaries: Unlike definite integrals, indefinite integrals do not have upper and lower limits of integration.
• Symbolic Representation: The notation ∫f(x)dx means "find the antiderivative of f(x)". The "dx" indicates the variable of integration and is the differential form of the function.
💡Example
To find the indefinite integral of f(x) = x²:
• Recall the power rule for integration: ∫xⁿ dx = xⁿ⁺¹/(n+1) + C.
• Apply the rule to x²: ∫x² dx = x²⁺¹/(2+1) + C = x³/3 + C.
• The result, x³/3 + C, represents all functions whose derivative is x², such as x³/3, (x³/3) + 5, or (x³/3) - 10.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Indefinite integrals, power rule
01:28 Elementary antiderivatives
02:40 Antiderivatives of tan, cot, sec, cosec
04:15 Antiderivatives of inverse trig functions
05:34 Antiderivatives of log and exponential functions
07:00 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
39
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
DrOfEng
Integration by substitution is a calculus technique to solve integrals of composite functions, acting as the reverse of the chain rule for differentiation. The method involves substituting a part of the integrand with a new variable (often u) to simplify the integral. You identify a function and its derivative within the integrand, set the function as u, then find du (the derivative of u with respect to x multiplied by dx). This transforms the integral into a simpler form, ∫f(u)du, which can be integrated using basic rules. Finally, you substitute the original function back for u to get the antiderivative in terms of the original variable.
💡Steps for Integration by Substitution
• Identify the substitution: Look for an inner function, g(x), whose derivative, g'(x), is also a factor in the integrand.
• Choose u: Let u = g(x).
• Find du: Differentiate u with respect to x to find du/dx, then rearrange to du = g'(x) dx.
• Rewrite the integral: Substitute u and du into the original integral.
• Integrate with respect to u: Solve the new, simpler integral using standard integration rules.
• Substitute back: Replace u with the original function g(x) to get the final answer.
💡Example
Let's integrate ∫ 2x cos(x²) dx:
• Identify: The function cos(x²) has an inner function x², and its derivative is 2x, which is also in the integral.
• Choose u: Let u = x².
• Find du: du/dx = 2x, so du = 2x dx.
• Rewrite: ∫ 2x cos(x²) dx becomes ∫ cos(u) du.
• Integrate: ∫ cos(u) du = sin(u) + C.
• Substitute back: Replace u with x² to get sin(x²) + C.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Integration by substitution
01:12 u-substitution, definite integrals
02:08 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
40
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
DrOfEng
Integration using long division is a technique to integrate improper rational functions, where the degree of the numerator is greater than or equal to the degree of the denominator. The process involves performing polynomial long division to rewrite the integrand as a polynomial plus a proper rational function (where the numerator's degree is less than the denominator's). The polynomial part is integrated directly using basic rules, while the proper rational function part is then integrated using other methods, such as partial fraction decomposition or completing the square.
💡When to Use Long Division for Integration
• Improper Rational Functions: Use this method when you're faced with an integral containing a rational expression (a fraction of polynomials) where the numerator's degree is greater than or equal to the denominator's degree.
💡Steps for Integration Using Long Division
• Perform Long Division: Divide the numerator by the denominator to find the quotient and remainder.
• Rewrite the Integrand: Express the original rational function as the quotient plus the remainder divided by the divisor.
∘ Original integrand = Quotient + (Remainder / Divisor)
• Integrate Term by Term: The integral can now be broken down into the integral of the polynomial (quotient) and the integral of the proper rational function (remainder/divisor).
∘ ∫ (Numerator/Denominator) dx = ∫ (Quotient) dx + ∫ (Remainder/Divisor) dx
• Integrate the Polynomial: The integral of the polynomial quotient is found using the power rule for integration.
• Integrate the Proper Rational Function: The remaining integral, which is now a proper rational function, can be integrated using techniques like:
• Partial Fraction Decomposition: If the denominator can be factored into simpler linear or irreducible quadratic factors.
• Completing the Square: If the denominator is an irreducible quadratic, completing the square can transform it into a form suitable for arctangent integrals or logarithmic forms.
• U-Substitution: U-substitution might be used to simplify the integral of the proper rational piece.
💡Example
To integrate ∫ (x³ + 3x² + 8x + 19) / (x² + 5) dx, you would first perform long division.
• Long Division: Divide x³ + 3x² + 8x + 19 by x² + 5, yielding a quotient of (x + 3) and a remainder of (3x + 4).
• Rewrite: The integral becomes ∫ (x + 3 + (3x + 4)/(x² + 5)) dx.
• Integrate:
∘∫ (x + 3) dx = x²/2 + 3x
∘∫ (3x / (x² + 5)) dx + ∫ (4 / (x² + 5)) dx
∘These remaining integrals are solved using u-substitution and arctangent integration, respectively, resulting in (3/2)ln(x² + 5) and (4/√5)arctan(x/√5).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Integration by polynomial long division
01:02 Worked Example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
41
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
DrOfEng
Integration by completing the square is a method for evaluating integrals with quadratic expressions in the denominator, particularly when the quadratic is irreducible (cannot be factored into real linear terms). The process involves rewriting the quadratic \(ax^{2}+bx+c\) into the form \(a(x+k_{1})^{2}+k_{2}\), which is then manipulated using u-substitution into a standard integral form, typically involving the inverse tangent (\(\arctan \)) or inverse sine (\(\arcsin \)) functions.
💡Steps for Completing the Square
• Ensure x² coefficient is one: If the coefficient of \(x^{2}\) (let's call it \(a\)) is not 1, factor it out from the entire quadratic expression.
∘ For example, \(2x^{2}-4x+11\) becomes \(2(x^{2}-2x+\frac{11}{2})\).
• Complete the square on the remaining quadratic: Take the coefficient of the \(x\) term (let's call it \(b^{\prime }\)), divide it by 2, and then square the result. Add and subtract this value inside the parenthesis.
∘ For example, in \(x^{2}-2x+\frac{11}{2}\), the \(x\) coefficient is -2.
∘ Half of -2 is -1, and squaring it gives 1.
∘ The expression becomes \(2(x^{2}-2x+1+\frac{11}{2}-1)\).
• Factor the perfect square trinomial: The first three terms inside the parenthesis now form a perfect square trinomial, \((x+b^{\prime }/2)^{2}\).
∘ \(2((x-1)^{2}+\frac{9}{2})\).
• Simplify the constant term: Combine the remaining constant terms.
∘ \(2((x-1)^{2}+\frac{9}{2})=2(x-1)^{2}+9\).
💡Applying to Integrals
• Rewrite the denominator: Substitute the completed square form into the integral.
∘ For example, \(\int \frac{1}{2x^{2}-4x+11}dx\) becomes \(\int \frac{1}{2(x-1)^{2}+9}dx\).
• Use substitution: Let \(u\) be the term in the parenthesis. In the example, \(u=x-1\), so \(du=dx\).
∘ The integral becomes \(\int \frac{1}{2u^{2}+9}du\).
• Manipulate to match standard forms: Factor out constants and rearrange the expression to match a known integral, often involving the form \(\frac{1}{a^{2}+u^{2}}\).
∘ \(\int \frac{1}{2u^{2}+9}du=\frac{1}{2}\int \frac{1}{u^{2}+(3/\sqrt{2})^{2}}du\).
• Integrate: Apply the appropriate integral formula.
∘ The integral \(\int \frac{1}{a^{2}+x^{2}}dx=\frac{1}{a}\arctan (\frac{x}{a})+C\).
∘ The final result can be converted back to the original variable.
💡When to Use This Method
• Irreducible quadratics: This method is essential for integrals involving quadratic denominators that do not factor into real linear terms.
• Non-standard forms: It is useful for integrands that resemble natural logarithms or inverse trigonometric functions but are "off" due to the quadratic expression.
• Standard forms: Completing the square transforms a general quadratic into a form that can be solved using known integration techniques, such as those found in integral tables.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Completing the square
00:40 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
42
Integration by Parts, Formula, Rule, Example, Order - Calculus
DrOfEng
Integration by parts is a calculus technique to integrate the product of two functions, derived from the product rule for differentiation. It transforms a complex integral into simpler ones, using the formula: ∫u dv = uv - ∫v du. To apply it, you select a function to be 'u' (which will be differentiated) and the rest as 'dv' (which will be integrated), often guided by the LIATE mnemonic to choose 'u' such that its derivative simplifies, and 'dv' such that its integral is easily found.
💡The Formula
The integration by parts formula is: ∫u dv = uv - ∫v du
💡When to Use It
This method is particularly useful for integrating products of functions, such as:
• A logarithmic function multiplied by an algebraic function.
• A trigonometric function multiplied by an algebraic function.
• An algebraic function multiplied by an exponential function.
💡Steps to Apply the Formula
• Identify u and dv: From the product of functions to be integrated, choose a function 'u' and the remaining part as 'dv'.
• Find du and v: Differentiate 'u' to find 'du' and integrate 'dv' to find 'v'.
• Apply the formula: Substitute 'u', 'v', 'du', and 'dv' into the integration by parts formula.
• Simplify: Evaluate the new, hopefully simpler, integral.
💡How to Choose u and dv (The LIATE Rule)
The acronym LIATE can help decide which function to choose for 'u':
• L: ogarithmic functions (e.g., ln(x))
• I: nverse trigonometric functions (e.g., arcsin(x))
• A: lgebraic functions (e.g., x, x²)
• T: rigonometric functions (e.g., sin(x), cos(x))
• E: xponential functions (e.g., e^x)
The function that appears earliest in this list should generally be chosen as 'u'.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Integration by parts
01:05 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
43
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
DrOfEng
Integration using partial fractions is a method to solve integrals of complex rational functions by breaking them down into simpler fractions whose integrals are easier to find, typically using logarithms. The process involves decomposing the integrand into partial fractions, solving for the unknown constants in the numerator of these fractions, and then integrating each simplified fraction.
💡Steps for Integration by Partial Fractions
• Ensure Proper Rational Function: The degree of the numerator must be less than the degree of the denominator. If it's not, perform polynomial long division first to obtain a proper fraction.
• Factor the Denominator: Factor the denominator of the rational function into its simplest components, such as distinct linear factors, repeated linear factors, irreducible quadratic factors, and repeated irreducible quadratic factors.
• Set up the Partial Fraction Decomposition: Write the original rational function as a sum of partial fractions, with appropriate numerators over each factor.
∘ For a distinct linear factor (ax+b), the term is A/(ax+b).
∘ For a repeated linear factor (ax+b)ⁿ, the terms are A₁/(ax+b) + A₂/(ax+b)² + ... + Aₙ/(ax+b)ⁿ.
∘ For an irreducible quadratic factor (ax²+bx+c), the term is (Ax+B)/(ax²+bx+c).
• Solve for the Constants: Equate the original numerator with the sum of the numerators of the partial fractions. Solve this equation for the unknown constants (A, B, etc.) by either substituting convenient values for x or by comparing coefficients of like powers of x.
• Integrate the Simpler Fractions: Substitute the found partial fractions back into the integral and integrate each term separately.
∘ Integrals of the form ∫(A/(ax+b)) dx typically result in A/a * ln|ax+b| + C.
∘ Add the constant of integration, C, for indefinite integrals.
💡Example
• To integrate (6x+13)/(x²+5x+6), you would first factor the denominator as (x+2)(x+3). Then, you would set up the decomposition:
(6x+13)/((x+2)(x+3)) = A/(x+2) + B/(x+3).
• Solving for A and B gives A = 7 and B = -1.
• So the integral becomes:
∫(7/(x+2) - 1/(x+3)) dx
• This can be integrated as: 7 ln|x+2| - ln|x+3| + C
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Integration using partial fractions, distinct factors
01:24 Repeated factors
03:42 Irreducible quadratic
05:21 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
44
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
DrOfEng
Improper integrals extend definite integrals to situations with an infinite integration interval or a function with a discontinuity within the interval. They are evaluated by replacing the problematic limit (infinity or a discontinuity) with a variable, say 't', and then calculating the definite integral from that variable to the other limit. The key is to take the limit as the variable 't' approaches the infinite or problematic value. If the limit results in a finite number, the integral converges; if the limit does not exist or is infinite, the integral diverges.
💡Two Types of Improper Integrals
• Type 1: Infinite Limits of Integration
∘Description: This type involves integrating over an interval that extends to infinity, such as from a finite number to positive or negative infinity, or between two infinite limits.
∘Example: The integral of 1/x² from 1 to infinity: ∫₁^∞ (1/x²) dx.
∘Evaluation:
⬩Replace the infinite limit with a variable (e.g., 'b'): lim (b→∞) ∫₁^b (1/x²) dx.
⬩Evaluate the definite integral: ∫₁^b (1/x²) dx = [-1/x]₁^b = -1/b - (-1/1) = 1 - 1/b.
⬩Take the limit as 'b' approaches infinity: lim (b→∞) (1 - 1/b) = 1.
⬩Conclusion: Since the limit is a finite number (1), the integral converges.
• Type 2: Integrands with a Discontinuity
∘Description: This type of integral occurs when the function being integrated has a vertical asymptote or some other form of discontinuity within the interval of integration.
∘Example: The integral of 1/x from 0 to 1: ∫₀¹ (1/x) dx, where x=0 is a point of discontinuity.
∘Evaluation:
⬩The approach from the left for the discontinuity.
⬩Replace the problematic limit (0) with a variable (e.g., 'a') and take the limit: lim (a→0⁺) ∫ₐ¹ (1/x) dx.
⬩Evaluate the definite integral: ∫ₐ¹ (1/x) dx = [ln|x|]ₐ¹ = ln|1| - ln|a| = 0 - ln|a| = -ln|a|.
⬩Take the limit as 'a' approaches 0 from the right: lim (a→0⁺) (-ln|a|) = ∞.
⬩Conclusion: Since the limit is infinity, the integral diverges.
💡Convergence vs. Divergence
• Convergent: An improper integral is convergent if the limit of the corresponding definite integral exists and is a finite number.
• Divergent: An improper integral is divergent if the limit does not exist or is infinite.
By using limits, improper integrals allow us to determine if an unbounded area under a curve or an area with a discontinuity can be represented by a finite value.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Improper integrals
01:31 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
45
Selecting Integration Techniques Explained, List of Methods - Calculus
DrOfEng
To select the right integration technique, start by simplifying the integrand and trying a simple u-substitution. If that doesn't work, identify the integral's type: a product of functions suggests integration by parts or tabular integration, while rational functions may require partial fractions. Other advanced methods include trigonometric substitution for expressions involving sums or differences of squares, and trigonometric integrals for simplifying trig functions. If the initial method fails, consider trying a combination of techniques.
💡General Steps for Choosing an Integration Technique
• Simplify the Integrand: Before anything else, try to simplify the function you are integrating using algebraic manipulation or trigonometric identities.
• Try a Simple Substitution (u-Substitution): Look for a function and its derivative (or something that can be made into its derivative with a constant multiplier) within the integrand.
• Identify the Form of the Integral:
∘Product of Functions: If you have a product, consider Integration by Parts. Tabular integration is a fast version of this if one factor's derivative eventually becomes zero.
∘Rational Functions: If you have a rational function (a polynomial divided by another polynomial), partial fraction decomposition is often effective.
∘Sums/Differences of Squares: For expressions like \(a^{2}\pm x^{2}\) or \(x^{2}\pm a^{2}\), consider a trigonometric substitution.
∘Trigonometric Functions: Look for patterns in powers of sine and cosine or use identities to simplify.
• Apply the Appropriate Technique: If a simple substitution doesn't work, move to the more advanced techniques based on the identified form.
• Try Combinations: Complex integrals may require a sequence of different techniques. For example, you might use u-substitution to simplify the integrand, then integration by parts.
💡When to Use Specific Techniques
• U-Substitution: Use for integrals where the derivative of a part of the integrand is also present.
• Integration by Parts: Use when you have a product of two functions, especially when u-substitution fails.
• Partial Fractions: Use for integrating rational functions where the denominator can be factored.
• Trigonometric Substitution: Use for integrals containing expressions like \(\sqrt{a^{2}-x^{2}}\), \(\sqrt{a^{2}+x^{2}}\), or \(\sqrt{x^{2}-a^{2}}\).
• Trigonometric Integrals: Use for simplifying integrals involving powers of sine and cosine by using trigonometric identities.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Selecting integration techniques
02:02 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
1
comment
46
Intro to Differential Equations, Modelling - Calculus
DrOfEng
This calculus video covers a tutorial which provides an introduction to differential equations and modelling.
47
Verifying Solutions to Differential Equations - Calculus
DrOfEng
This calculus video covers a tutorial on verifying if a function is a solution to a differential equation.
1
comment
48
Sketching Slope Fields, Differential Equations - Calculus
DrOfEng
This calculus video covers a tutorial on sketching slope fields for differential equations.
0:00 Intro to slope fields
1:01 Worked example on sketching slope fields
1
comment
49
Sketching Solution Curves, Slope Fields - Calculus
DrOfEng
This calculus video covers a tutorial on sketching solution curves for differential equations using slope fields.
1
comment
50
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
DrOfEng
This video explains Euler's formula, including definition, step size, examples, and what it is used for. In this case, it is used to approximate solutions to first order ordinary differential equations.
1
comment
51
Separation of Variables, General Solution, ODEs - Calculus
DrOfEng
This video explains the separation of variables method for solving differential equations, including example practice problems. You will understand how to separate the variables and know when to use this method.
3
comments
52
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
DrOfEng
This video explains the separation of variables method for solving differential equations, including example practice problems. You will understand how to separate the variables and know when to use this method.
0:00 Separation of variables, particular solution
2:04 Worked examples
1
comment
53
Exponential Models, Growth, Decay, Differential Equations - Calculus
DrOfEng
This video explains exponential models with differential equations, including example applications like population growth, formula and what they predict.
0:00 Modelling exponential growth and decay using ODEs
1:41 Worked examples on exponential growth and decay
54
Logistic Growth Model, Differential Equations - Calculus
DrOfEng
This video explains the logistic population growth mathematical model, including the differential equation, solution curve, function, graph, rate, and formula.
0:00 Intro to the logistic growth model
1:40 Finding a particular solution
2:53 Verifying the carrying capacity
3:54 Time at the maximum population growth rate
7
comments
55
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
DrOfEng
This video explains the mean value theorem (MVT) formula and definition for integrals using an informal geometric proof, what it is, how do you know if it applies and what it is used for.
56
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
DrOfEng
This video explains the meaning of displacement and difference to distance, simple definition of speed and velocity, and how acceleration is calculated.
0:00 Connecting position, velocity and acceleration using graphs and integrals
2:17 Worked examples
1
comment
57
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
DrOfEng
The video explains what is and how to apply a definite integral in context with example problems. You will understand what does it mean in simple terms and real world situations that involve definite integrals, as well as the meaning of formulas of accumulation functions.
0:00 Definite integrals in applied contexts
1:35 Worked examples
1
comment
58
Definite Integrals, Area Between Curves, Functions of x - Calculus
DrOfEng
How to find the area under the curve or between curves by integration. What the value (can be negative) or formula means or refers to is dependent on the application. Rectangles perpendicular to the x axis tell you that the integral is with respect to x.
0:00 Finding areas between curves using definite integrals
0:52 Worked examples
4
comments
59
Definite Integrals, Area Between Curves, Functions of y - Calculus
DrOfEng
How to find the area under the curve or between curves by integration. What the value (can be negative) or formula means or refers to is dependent on the application. Rectangles perpendicular to the y axis tell you that the integral is with respect to y.
0:00 Finding areas between curves using definite integrals
1:25 Worked examples
60
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
DrOfEng
Why the definite integral is the area under a curve or between two curves using examples. Understanding the meaning and properties of the formula or equation, if it gives the negative or net area, making appropriate substitutions for the limits of integration and how to solve area problems using the definite integral.
0:00 Finding areas between curves using definite integrals
1:35 Worked examples
1
comment
61
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
DrOfEng
How to find the volume of a prism with a constant cross-section or solid object with a cross section using integration. Basic geometry is used to derive the square cross-section formula. Worked examples and practice problems are covered for visualization. Square cross sections are covered while triangles (e.g. isosceles) and semicircles are deferred to another tutorial.
0:00 Finding the volume of solids with cross-sections using definite integrals
1:19 Worked examples
62
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
DrOfEng
How to find the volume of a prism with a constant cross-section or solid object with a cross section using integration. Basic geometry is used to derive the triangle and semi-circle cross-section formula. Worked examples and practice problems are covered for visualization. Triangle (equilateral and isosceles) and semicircle cross sections are covered.
0:00 Volume of solids with triangle cross-sections
3:25 Volume of solids with semicircle cross-sections
4:37 Worked examples
63
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
DrOfEng
Integration using the disc method to find the volume of solid of revolution (e.g. sphere and cone proof), and what it is. Examples show how to know when to use it (e.g. vs the washer or shell method), what is the R, integral formula about x axis and y axis, and derive the formula to calculate the volume of a sphere and cone.
0:00 Volume with disk method
1:53 Worked examples
64
Volume with the Disk Method, Revolving Around other Axes - Calculus
DrOfEng
Integration using the disc method to find the volume of solid of revolution, and what it is. Examples show how to know when to use it (e.g. vs the washer or shell method), what is the R, integral formula about other axes.
0:00 Volume with disk method
1:44 Worked example
65
Washer Method to Find the Volume of a Revolved Solid - Calculus
DrOfEng
This video explains the washer method vs the disk method, including what it is, when to use it, and how to find the radius. You will understand the difference to the disk method. The washer method around a line and shell method are deferred to another tutorial.
0:00 Volume with the washer method
1:29 Worked examples
66
Volume with the Washer Method, Revolved Solid Around Line - Calculus
DrOfEng
This video explains the washer method to find the volume of a revolved solid around a vertical and horizontal line using integration. You will understand the difference to the disk method.
0:00 Volume with the washer method
1:42 Worked examples
1
comment
67
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
DrOfEng
This video explains the arc length integral formula in Cartesian coordinates, including examples on determining the arc length of a line and other curves.
0:00 Deriving the integral
2:06 Worked examples
68
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
DrOfEng
This video explains how to use the shell method to calculate the volume of a solid of revolution, including integral formula, equation, practice example problems (x and y axis). You will understand the difference between the washer and shell method.
0:00 Volume with the shell method
1:41 Practice example problems
1
comment
69
Parametric Equations, Definition, Differentiation - Calculus
DrOfEng
This video explains the meaning of parametric equations (eq), including what they are with example practice questions, the rule, how do you differentiate them and how to determine if the parametric form is differentiable. You will understand how they can be applied to determine the distance traveled and direction of motion. Converting an equation to parametric form is deferred to another tutorial.
0:00 Parametric equations, definition and differentiation
1:21 Worked examples
70
Parametric Equations, Second Derivative - Calculus
DrOfEng
This video explains the meaning of parametric equations (eq), including what they are with example practice questions, the rule, how do you differentiate them (2nd derivative) and how to determine if the parametric form is twice differentiable. You will understand how they can be applied to determine the distance traveled and direction of motion. Converting an equation to parametric form is deferred to another tutorial.
0:00 Parametric equations, second derivative
1:13 Worked example
1
comment
71
Parametric Curve, Arc Length, Distance - Calculus
DrOfEng
This video explains how to find the arc length of a parametric curve (e.g. y = 2x), including equations, formula and example. You will understand what it means in the context of distance traveled by a particle.
0:00 Parametric curve, arc length
1:59 Worked example
72
Vector-Valued Functions, Differentiation, Examples - Calculus
DrOfEng
This video explains vector valued functions including definition, formula, problems and solutions, parameterization and graphing. You will understand what it is and how do you evaluate it. Motion in space is deferred to another tutorial.
0:00 Definition
1:43 Differentiation
3:47 Worked examples
2
comments
73
Vector-Valued Function, Integration - Calculus
DrOfEng
This video explains how to integrate a vector valued function, including indefinite integral and practice problems. You will understand if you can integrate it and what it is. Derivatives and how do you turn a vector valued function into a scalar function are covered in other tutorials.
0:00 Integration of vector-valued function
1:32 Worked example
1
comment
74
Vector-Valued Functions and Motion in 2D Space - Calculus
DrOfEng
This video explains vector-valued functions in the context of solving motion problems, including position, velocity, speed and acceleration using differentiation, integration and arc length integrals, and worked example problems and solutions that involve projectile motion and uniform circular motion.
0:00 Vector-valued functions, solving motion problems
1:48 Worked examples
75
Polar Coordinates, Polar Curves, Differentiation - Calculus
DrOfEng
This video explains how to differentiate equations of polar curves, including equation, second derivative, and plotting polar curves like a cardioid, limacon and lemniscate.
0:00 Definition of polar coordinates
1:37 Polar curves
3:05 Differentiating polar equations
4:52 Worked examples, plotting polar curves
11:16 Worked examples, differentiating polar equations
76
Polar Curve, Area of Region, Integration - Calculus
DrOfEng
This video explains how do you find the area of a region in a polar curve using integration, including formula, graph, derived integral, and worked example practice problem.
0:00 Polar curve area integral
1:52 Worked example
77
Polar Curve, Area of Region between Two Curves, Examples - Calculus
DrOfEng
This video explains how to find the area of a region bounded by two polar curves (e.g. circle, limacon, lemniscate, cardioid) using integration, including formula, equations, and practice problems.
0:00 Area between two polar curves, integral
1:29 Worked examples
78
Conics in Polar Coordinates, Derivatives, Example - Calculus
DrOfEng
This video explains what is a conic section in polar form, including the derivation of the polar equation for an ellipse, hyperbola and parabola using the focus and directrix, practice problem, eccentricity, graphing, and focus at the pole or origin.
0:00 Revision on conic sections
2:06 Equation of a parabola
6:08 Equation of an ellipse
13:59 Equation of a hyperbola
20:15 Common polar equation
25:00 Worked example
1
comment
79
Infinite Sequence, Definition, Representations, Convergence - Calculus
DrOfEng
This video explains the meaning of infinite sequences, including sum formula, definition, graphical representation, examples, epsilon-delta limit and notation. You will understand how to distinguish between infinite and finite sequences, and how to determine convergence.
0:00 Into to infinite sequences
1:02 Convergence
2:20 Example on epsilon-delta limit
4:04 Worked examples
Infinite Series, Definition, Partial Sum, Convergence - Calculus
DrOfEng
This video explains what is meant by infinite series, including formula, sum, convergence and worked examples (e.g. geometric and telescoping series). You will understand how to tell if the series is finite or infinite and if it converges or diverges.
0:00 Definition, convergence
1:32 Examples
81
Geometric Series, Sum, Convergence - Calculus
DrOfEng
This video explains what a geometric series is, including formula, example, infinite sum, and rule. The difference between a geometric sequence (e.g. 1,2,4,8,16) and series (e.g. 1+2+4+8+16) that the series is the sum of the terms in the sequence.
0:00 Geometric series, definition, sum
2:09 Worked example
82
nth Term Test, Divergence, Infinite Series, Examples - Calculus
DrOfEng
This video explains the nth term test for determining if an infinite series diverges, including, sequence rule, limit formula, conditions, and practice problems (e.g. alternating series).
0:00 nth term test
1:00 Examples
83
Integral Test, Convergence, Infinite Series, Example - Calculus
DrOfEng
This video explains the integral test for convergence, including the rule, three conditions or requirements for convergence or divergence, and practice problem.
0:00 Integral test definition
1:38 Worked example
1
comment
84
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
DrOfEng
This video explains the harmonic series, including definition, how to derive the convergence conditions using the integral test, graph and formula. The harmonic series can be derived from the harmonics or standing waves in physics.
0:00 Harmonic series and p-series
1:33 Convergence conditions
3:37 Worked examples
85
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
DrOfEng
This video explains the comparison tests for infinite series, including the limit form, rules, practice problems, examples, definition, requirements, what does it say, what is the comp test, conditions (e.g. =0). You will understand when to use the DCT and LCT and what they involve the comparison of.
0:00 Direct comparison test conditions
1:04 Limit comparison test conditions
2:47 Worked examples
86
Alternating Series Test, Infinite Series - AP Calculus BC
DrOfEng
This video explains the alternating series test for convergence, including definition and worked example practice problem. The series diverges if any of the three conditions fail. Error bound and remainder are deferred to another tutorial.
0:00 Alternating series test, definition
1:06 Worked example
87
Ratio Test, Infinite Series, Convergence, Examples - Calculus
DrOfEng
This video explains the ratio test to determine if an infinite series converges or diverges, including the three conditions and practice problems.
0:00 Ratio test, definition
1:19 Worked examples
1
comment
88
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
DrOfEng
This video explains the absolute convergence test of an alternating series, including definition, absolute vs conditional convergence, and what it means in terms of rearranging series that converge absolutely.
0:00 Absolute and conditional convergence
0:59 Rearranging series
1:31 Worked examples
1
comment
89
Alternating Series, Error Bound - Calculus
DrOfEng
This video explains the error bound (or truncation error or remainder) of an alternating series, including how to calculate it, the difference between error and error bound, and a worked example practice problem.
0:00 Alternating series, error bound
0:51 Worked example
2
comments
90
Taylor Polynomials, Approximating Functions - Calculus
DrOfEng
This video explains Taylor polynomials, which are derived from Taylor series, including the formula and a worked example. The difference between Taylor and Maclaurin polynomials is a=0.
0:00 Definition of a Taylor polynomial
1:41 Worked example
91
Lagrange Error Bound, Taylor Polynomials - Calculus
DrOfEng
This video explains the Lagrange error bound in the approximation of Taylor series using Taylor polynomials, including formula or equation, what does it do, and example practice problems.
0:00 Lagrange error bound
1:53 Worked examples
1
comment
92
Power Series, Convergence - Calculus
DrOfEng
This video explains the power series, including radius and interval of convergence, checking for convergence using the ratio test, convergence at the endpoints, determining analytical functions using term-by-term differentiation and integration, and worked examples.
0:00 Power series, definition
1:33 Convergence conditions
3:39 Ratio test
5:13 Term-by-term differentiation
6:48 Term-by-term integration
8:01 Examples
93
Taylor Series, Maclaurin Series - Calculus
DrOfEng
This video explains the Taylor series, including expansion about x=a or x=0 (Maclaurin series), for elementary functions like e^x, sinx and cosx, how it they can be used to derive the Euler formula and geometric series, how to know if a function has a Taylor series (i.e. it must be continuous and infinitely differentiable at x=a), and examples.
0:00 Taylor and Maclaurin series, definition
1:52 Worked examples
1
comment
94
Representing Functions as Power Series - Calculus
DrOfEng
This video explains how functions can be represented using power series, including the use of the derivative and recognising the sum of a geometric series, and worked examples.
0:00 Representing functions as power series
1:11 Worked examples
95
Sum of Alternating Harmonic Series (-1)^(n+1)1/n = ln2 - Calculus
DrOfEng
This video explains how the sum of the alternating harmonic series is ln(2) with a basic proof, and also shows that rearranging this series, which is conditionally convergent, results in another sum.
0:00 Show that the sum of the alternating harmonic series is ln(2)
1:54 Sum of rearranged series
1
comment
Infinite Series, Definition, Partial Sum, Convergence - Calculus
9 months ago
91
Health & Science
Education
infinite series
calculus
infinite series calculus 2
convergence
infinite series partial sums limit and convergence
convergence of series
infinite series convergence
partial sums
convergence of infinite series tutor
This video explains what is meant by infinite series, including formula, sum, convergence and worked examples (e.g. geometric and telescoping series). You will understand how to tell if the series is finite or infinite and if it converges or diverges.
0:00 Definition, convergence
1:32 Examples
Loading comments...
-
 LIVE
LIVE
Nerdrotic
3 hours agoThe WitcHER DOA | Box Office Massacre | Massive Industry Layoffs - Friday Night Tights 378
562 watching -

vivafrei
1 hour agoEric Swalwell in Trouble Again? RFK Jr. "Reverses Course" on Tylenol & Autism? Arctic Frost & MORE!
16K9 -
 1:19:51
1:19:51
DeVory Darkins
3 hours agoNewsom EXPOSED after latest bombshell and Democrats pulls shocking stunt regarding shutdown
52.3K17 -
 25:29
25:29
Stephen Gardner
1 hour ago💣 Trump White House UNEXPECTED Move + Thune DESTROYS Schumer on Senate Floor!!
5.2K10 -
 LIVE
LIVE
Drew Hernandez
13 hours agoSPOOKY WOKE HAG CALLS FOR DEMS TO EMBRACE CELEBRATING EXECUTION OF CHARLIE KIRK?!
318 watching -
![MAHA News [10.31] - HHS Coup, Big Food Documentary, SNAP Scams, Microplastic Solutions](https://1a-1791.com/video/fwe2/d9/s8/1/w/q/m/v/wqmvz.0kob-small-MAHA-News-10.31.jpg) LIVE
LIVE
Badlands Media
14 hours agoMAHA News [10.31] - HHS Coup, Big Food Documentary, SNAP Scams, Microplastic Solutions
305 watching -
 1:10:12
1:10:12
The Quartering
3 hours agoFood Wars Begin! Terror Plot Foiled & Much More!
61.9K20 -
 1:09:50
1:09:50
The Culture War with Tim Pool
4 hours agoJamaica Hurricane Predicts POLE SHIFT, The END Is Nigh | The Culture War with Tim Pool
110K95 -
 2:44:08
2:44:08
Lara Logan
10 hours agoSHOTS FIRED: The Tyranny of Big Pharma Exposed with Dr. Sherri Tenpenny | EP 42 | Lara Logan
22K6 -
 1:01:45
1:01:45
Playback Request Live
2 hours agoPRL LIVE @ DREAMHACK!!
10.3K1