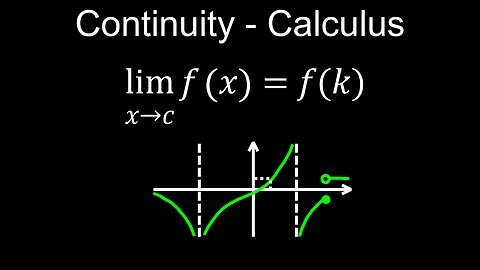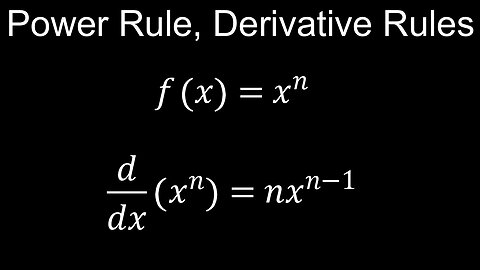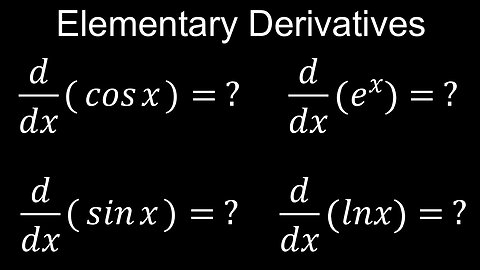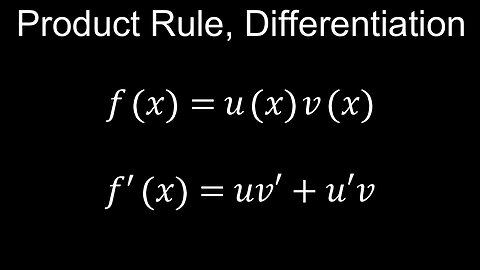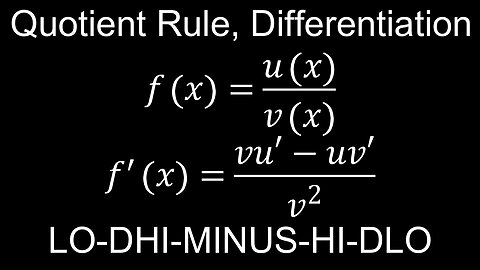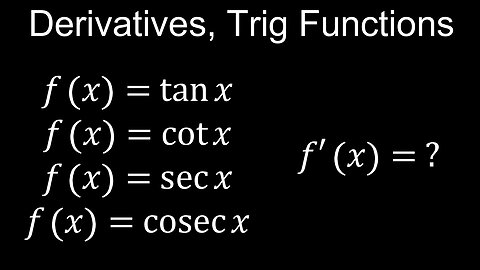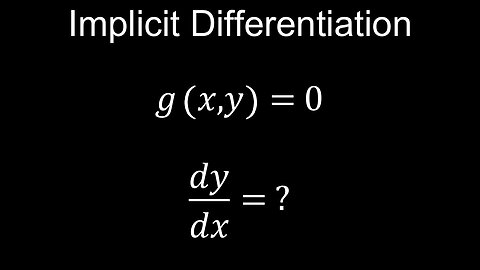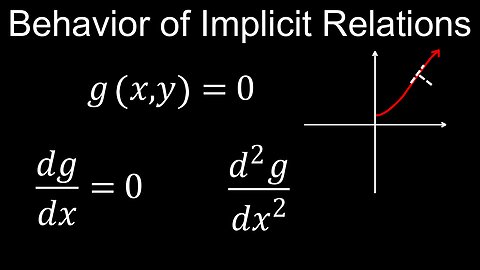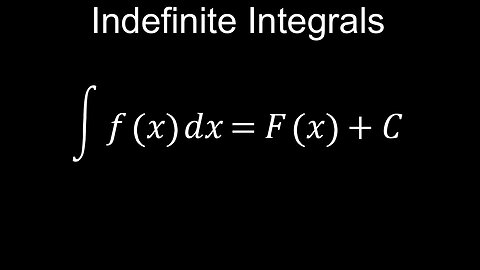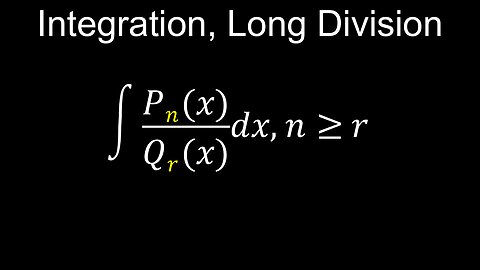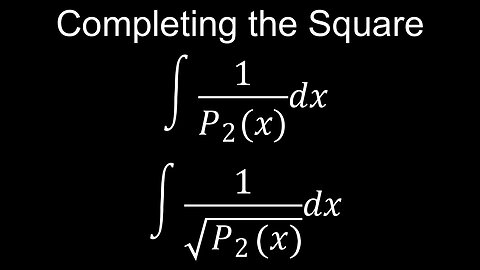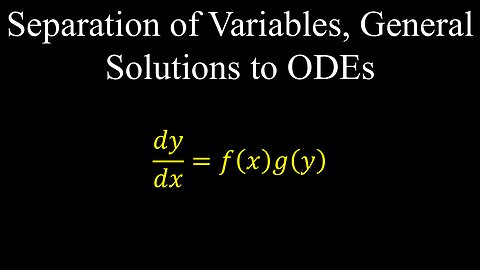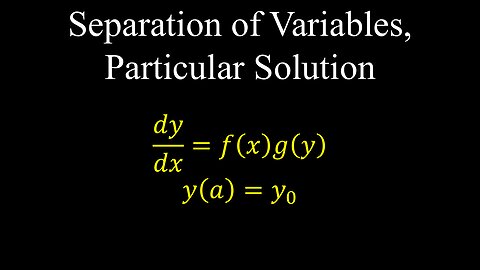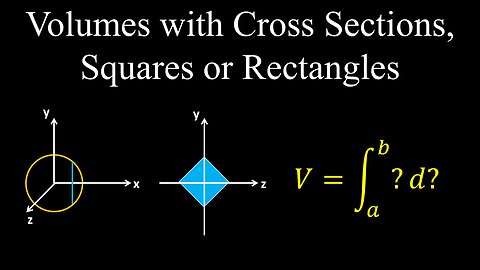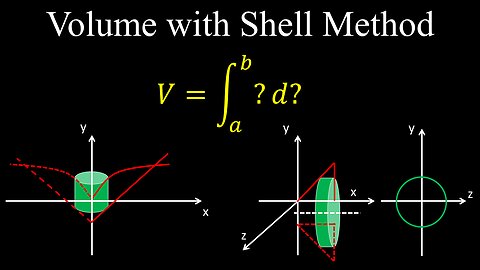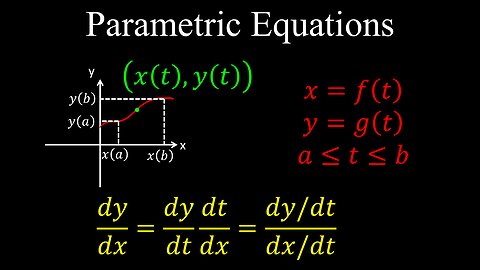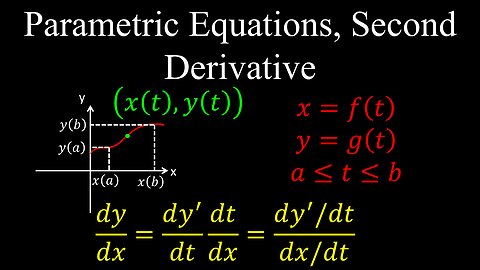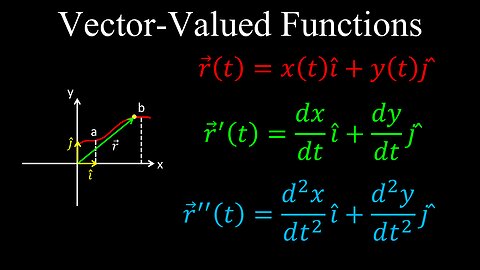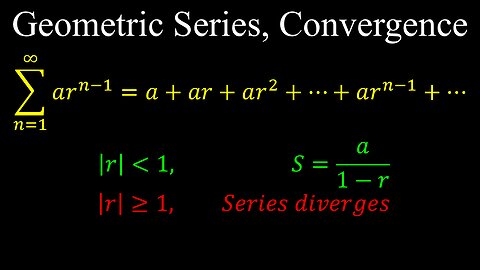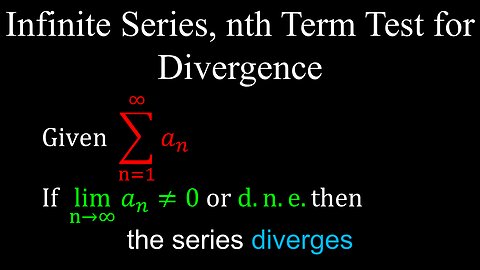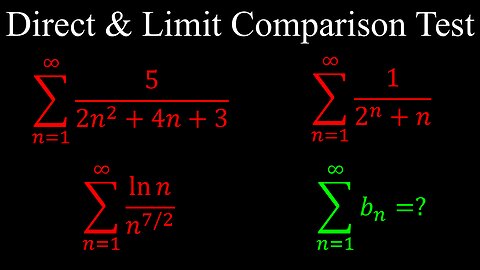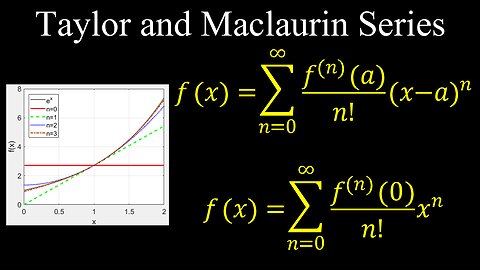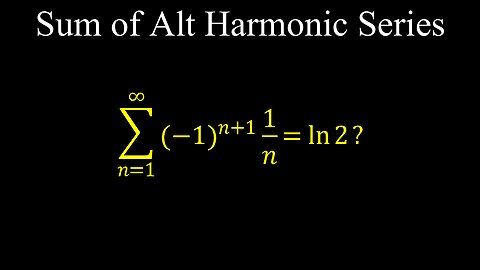Premium Only Content

Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
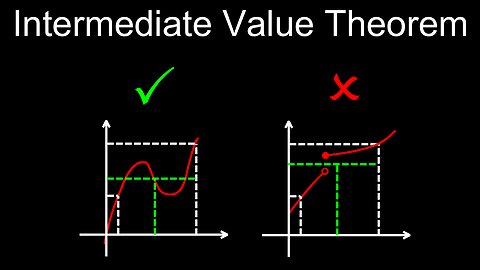
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
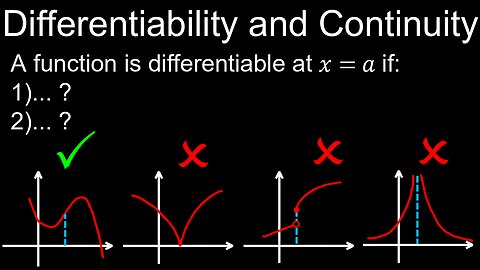
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
Derivative Rules, Power Rule for Differentiation - Calculus
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
Product Rule, Differentiation, Basic Proof, Examples - Calculus
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
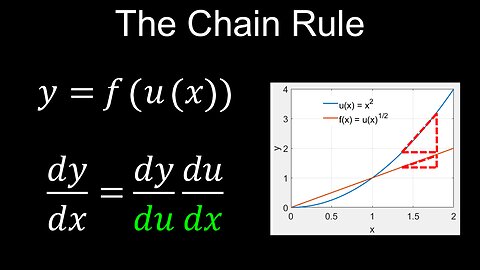
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
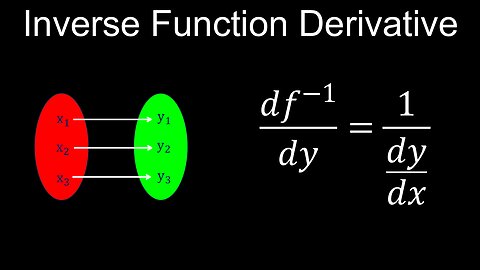
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
Derivatives in Context, Interpretation, Examples - Calculus
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
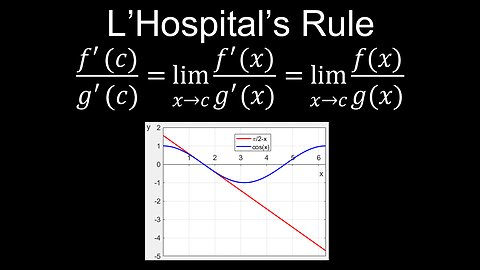
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
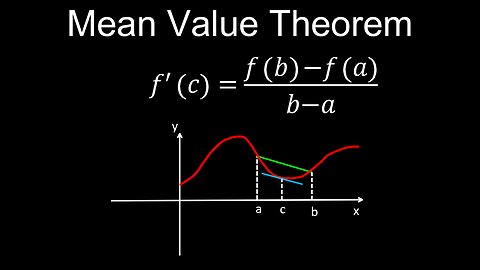
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
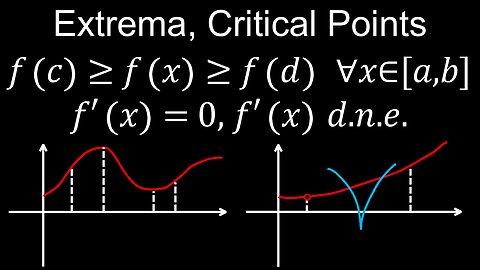
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
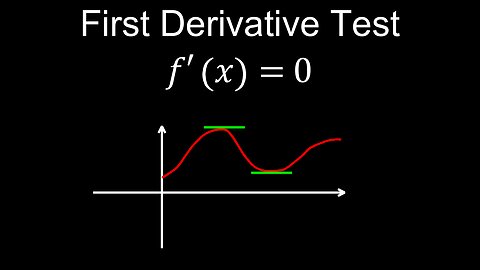
First Derivative Test, Local Extrema, Examples - Calculus
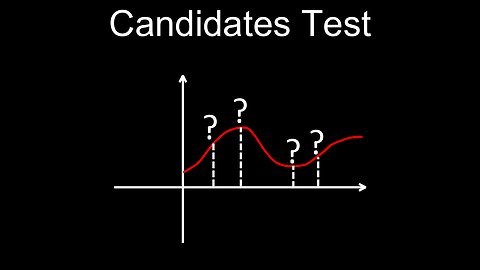
Candidates Test, Global Extrema, Example - Calculus
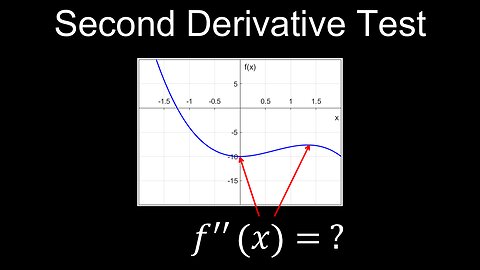
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
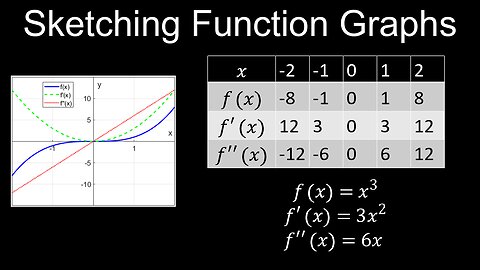
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
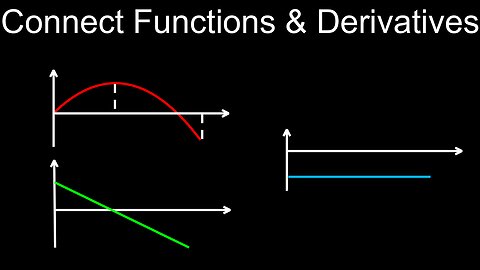
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
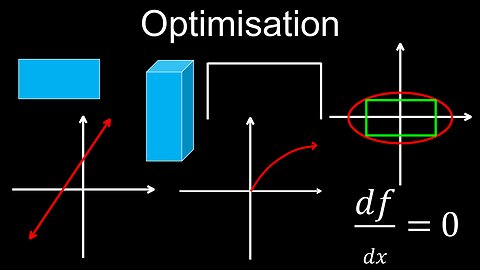
Solving Optimisation Problems, Differentiation, Examples - Calculus
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
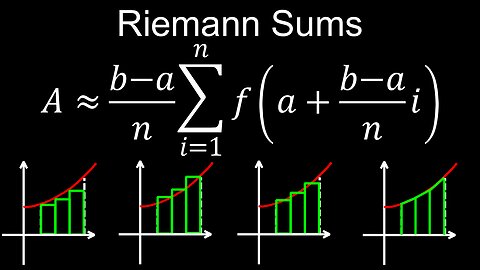
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
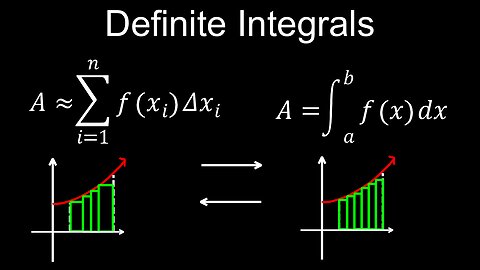
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
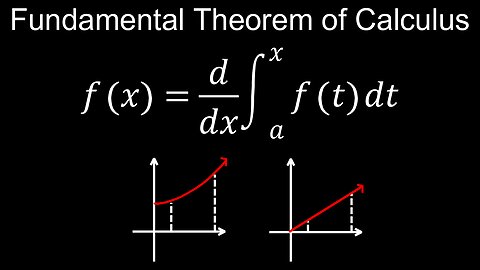
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
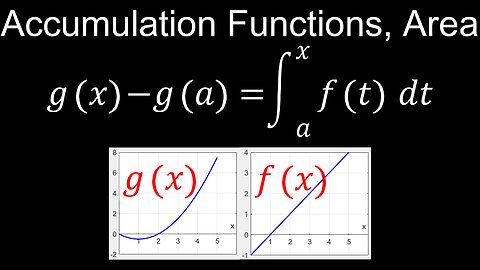
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by Parts, Formula, Rule, Example, Order - Calculus
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
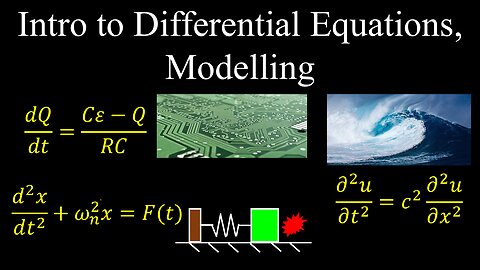
Intro to Differential Equations, Modelling - Calculus
Verifying Solutions to Differential Equations - Calculus
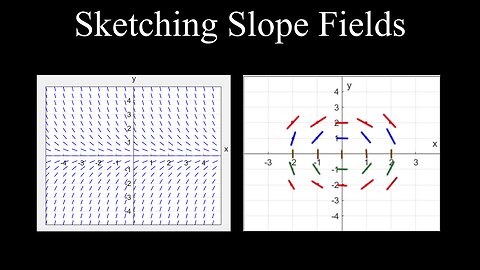
Sketching Slope Fields, Differential Equations - Calculus
Sketching Solution Curves, Slope Fields - Calculus
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
Separation of Variables, General Solution, ODEs - Calculus
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
Exponential Models, Growth, Decay, Differential Equations - Calculus
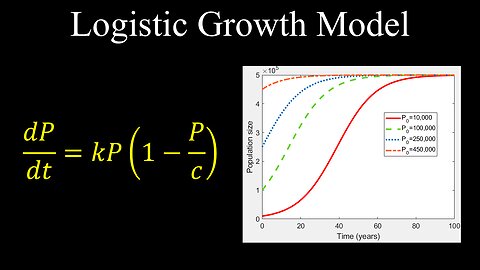
Logistic Growth Model, Differential Equations - Calculus
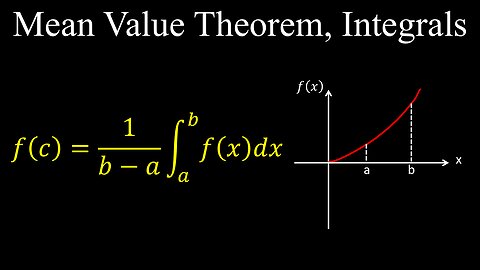
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
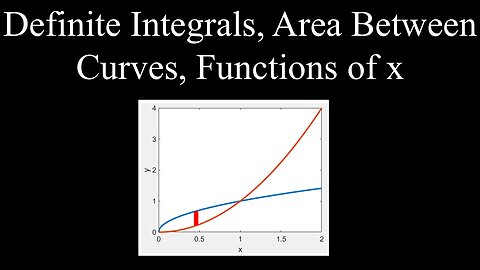
Definite Integrals, Area Between Curves, Functions of x - Calculus
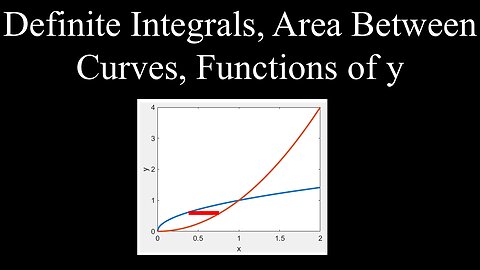
Definite Integrals, Area Between Curves, Functions of y - Calculus
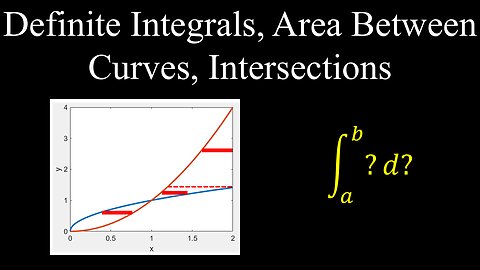
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
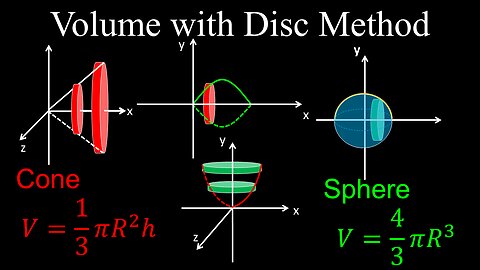
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
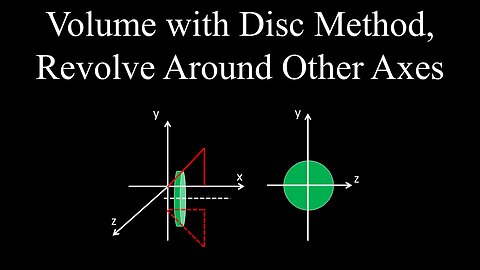
Volume with the Disk Method, Revolving Around other Axes - Calculus
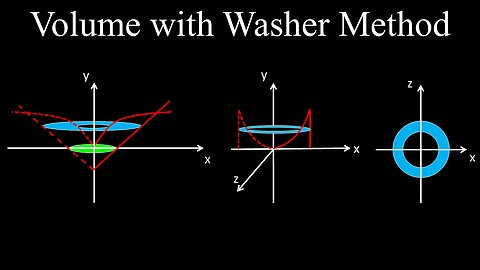
Washer Method to Find the Volume of a Revolved Solid - Calculus
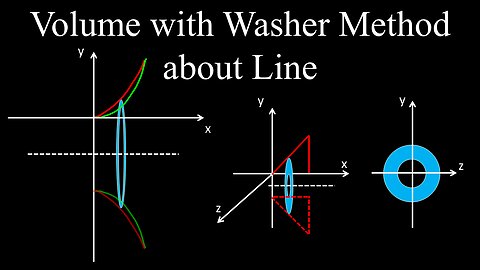
Volume with the Washer Method, Revolved Solid Around Line - Calculus
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
Parametric Equations, Definition, Differentiation - Calculus
Parametric Equations, Second Derivative - Calculus
Parametric Curve, Arc Length, Distance - Calculus
Vector-Valued Functions, Differentiation, Examples - Calculus
Vector-Valued Function, Integration - Calculus
Vector-Valued Functions and Motion in 2D Space - Calculus
Polar Coordinates, Polar Curves, Differentiation - Calculus
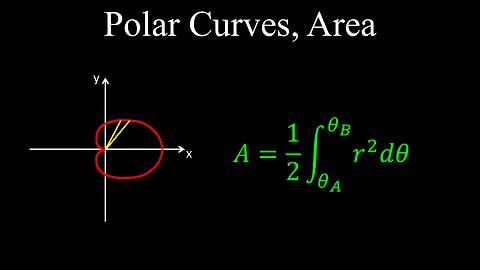
Polar Curve, Area of Region, Integration - Calculus
Polar Curve, Area of Region between Two Curves, Examples - Calculus
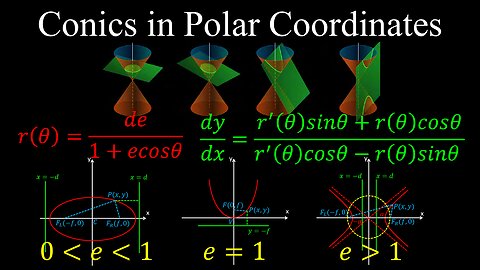
Conics in Polar Coordinates, Derivatives, Example - Calculus
Infinite Sequence, Definition, Representations, Convergence - Calculus
Infinite Series, Definition, Partial Sum, Convergence - Calculus
Geometric Series, Sum, Convergence - Calculus
nth Term Test, Divergence, Infinite Series, Examples - Calculus
Integral Test, Convergence, Infinite Series, Example - Calculus
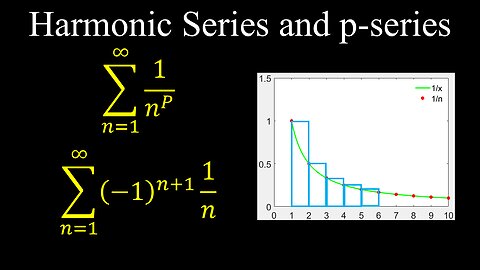
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
Alternating Series Test, Infinite Series - AP Calculus BC
Ratio Test, Infinite Series, Convergence, Examples - Calculus
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
Alternating Series, Error Bound - Calculus
Taylor Polynomials, Approximating Functions - Calculus
Lagrange Error Bound, Taylor Polynomials - Calculus
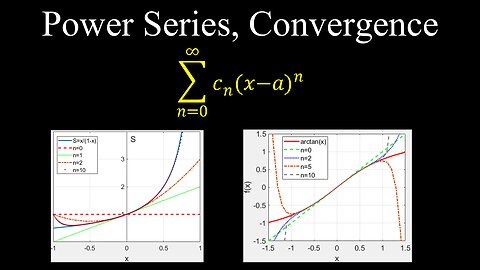
Power Series, Convergence - Calculus
Taylor Series, Maclaurin Series - Calculus
Representing Functions as Power Series - Calculus
Sum of Alternating Harmonic Series (-1)^(n+1)1/n = ln2 - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
To select the right integration technique, start by simplifying the integrand and trying a simple u-substitution. If that doesn't work, identify the integral's type: a product of functions suggests integration by parts or tabular integration, while rational functions may require partial fractions. Other advanced methods include trigonometric substitution for expressions involving sums or differences of squares, and trigonometric integrals for simplifying trig functions. If the initial method fails, consider trying a combination of techniques.
💡General Steps for Choosing an Integration Technique
• Simplify the Integrand: Before anything else, try to simplify the function you are integrating using algebraic manipulation or trigonometric identities.
• Try a Simple Substitution (u-Substitution): Look for a function and its derivative (or something that can be made into its derivative with a constant multiplier) within the integrand.
• Identify the Form of the Integral:
∘Product of Functions: If you have a product, consider Integration by Parts. Tabular integration is a fast version of this if one factor's derivative eventually becomes zero.
∘Rational Functions: If you have a rational function (a polynomial divided by another polynomial), partial fraction decomposition is often effective.
∘Sums/Differences of Squares: For expressions like \(a^{2}\pm x^{2}\) or \(x^{2}\pm a^{2}\), consider a trigonometric substitution.
∘Trigonometric Functions: Look for patterns in powers of sine and cosine or use identities to simplify.
• Apply the Appropriate Technique: If a simple substitution doesn't work, move to the more advanced techniques based on the identified form.
• Try Combinations: Complex integrals may require a sequence of different techniques. For example, you might use u-substitution to simplify the integrand, then integration by parts.
💡When to Use Specific Techniques
• U-Substitution: Use for integrals where the derivative of a part of the integrand is also present.
• Integration by Parts: Use when you have a product of two functions, especially when u-substitution fails.
• Partial Fractions: Use for integrating rational functions where the denominator can be factored.
• Trigonometric Substitution: Use for integrals containing expressions like \(\sqrt{a^{2}-x^{2}}\), \(\sqrt{a^{2}+x^{2}}\), or \(\sqrt{x^{2}-a^{2}}\).
• Trigonometric Integrals: Use for simplifying integrals involving powers of sine and cosine by using trigonometric identities.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Selecting integration techniques
02:02 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 3:10:46
3:10:46
Ellie_roe
3 hours agoEllie and Errys Halloween Spooktacular || Random Horror Games
778 -
 50:27
50:27
Sarah Westall
4 hours agoBig Banks Caught Rigging Market, IMF tells World to “Buckle Up” w/ Andy Schectman
9.46K1 -
 13:54
13:54
Degenerate Jay
11 hours ago5 Best Superhero Movies To Watch On Halloween
1.18K1 -
 59:03
59:03
NAG Podcast
4 hours agoSarah Fields: BOLDTALK W/Angela Belcamino
1.77K2 -
 1:21:41
1:21:41
Glenn Greenwald
7 hours agoGlenn Takes Your Questions: On the Argentina Bailout, Money in Politics, and More | SYSTEM UPDATE #541
63.4K37 -
 3:10:08
3:10:08
Barry Cunningham
4 hours agoPRESIDENT TRUMP TO USE NUCLEAR OPTION? FOOD STAMPS END! | SHUTDOWN DAY 31
27.4K21 -
 1:06:56
1:06:56
BonginoReport
12 hours agoThe Battle Between Good & Evil w/ Demonologist Rick Hansen - Hayley Caronia (Ep.168)
86.5K30 -
 1:12:57
1:12:57
Kim Iversen
6 hours agoBill Gates Suddenly Says “Don’t Worry About Climate Change”?
80.1K58 -
 1:05:12
1:05:12
Michael Franzese
7 hours agoI Waited 50 Years to Tell You What Happened on Halloween 1975
37.7K13 -
 1:07:15
1:07:15
Candace Show Podcast
7 hours agoINFILTRATION: Charlie Kirk Was Being Tracked For Years. | Candace Ep 256
81K311