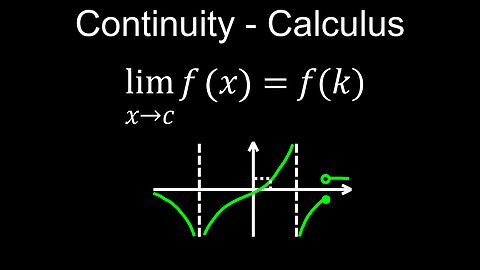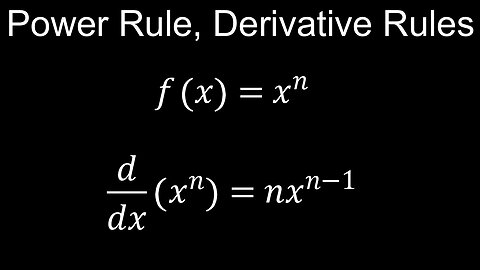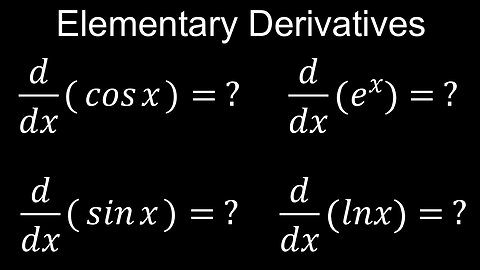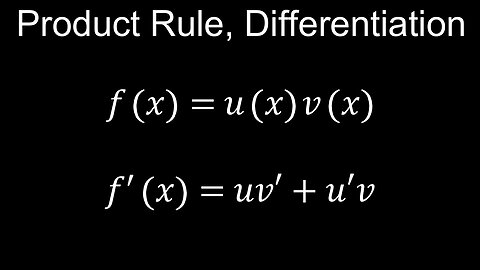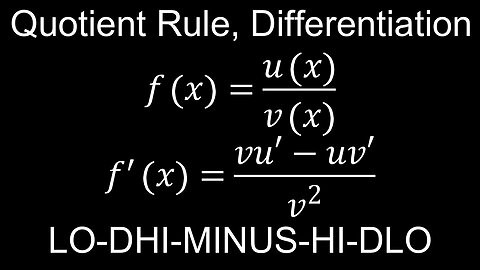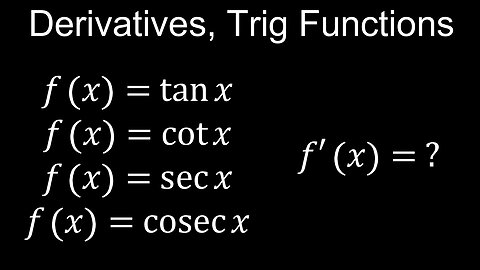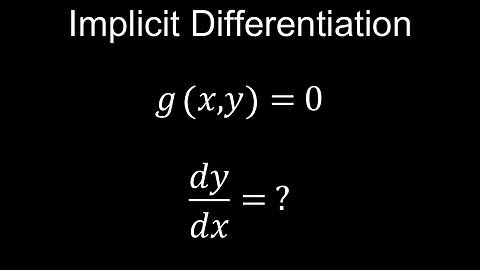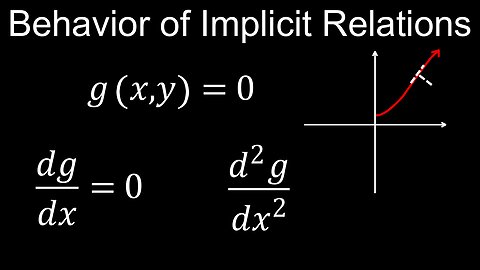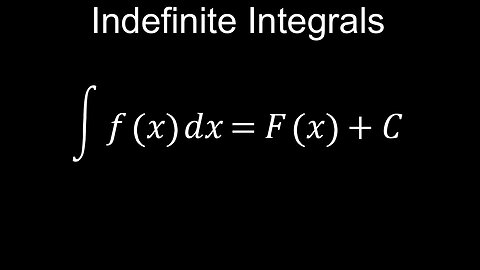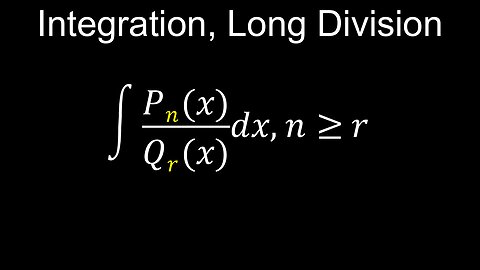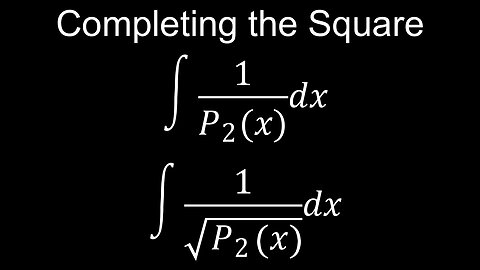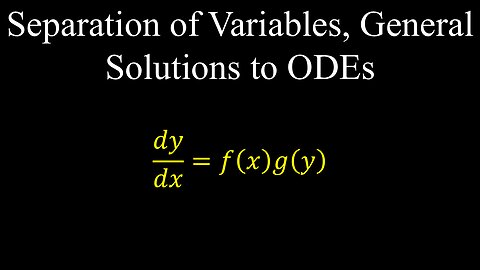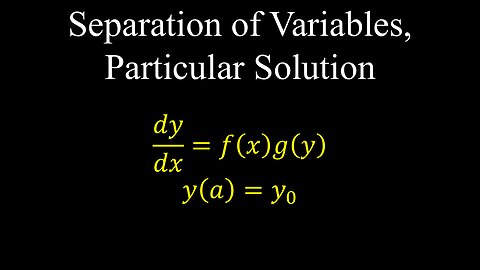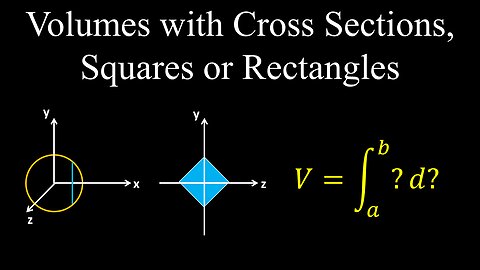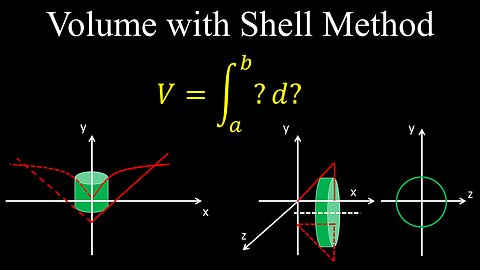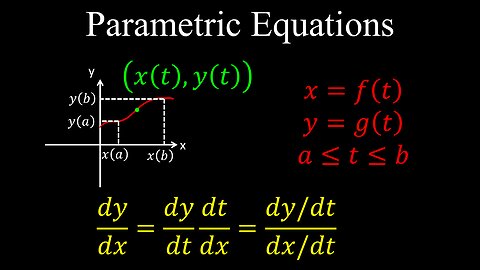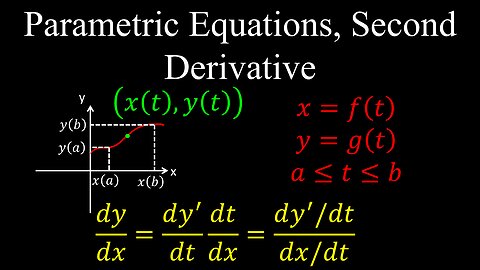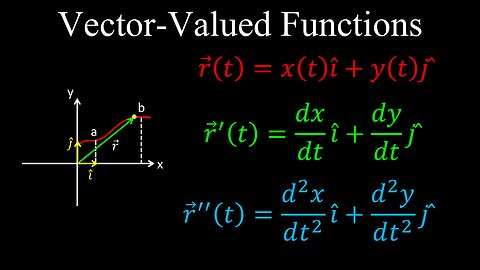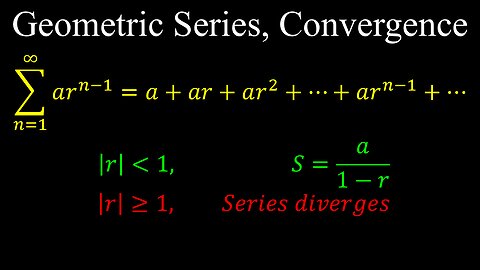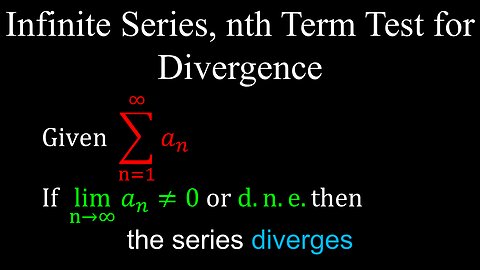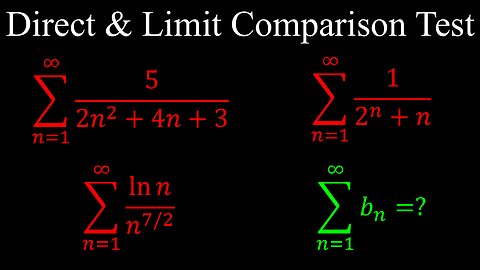Premium Only Content

Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
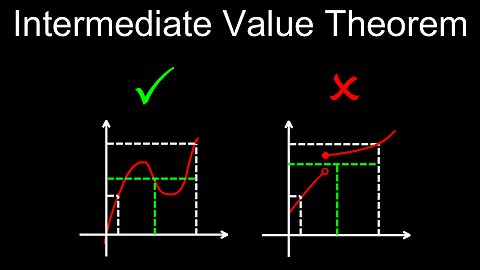
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
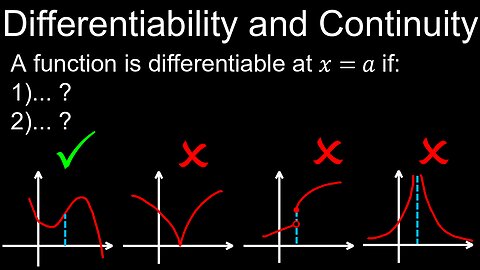
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
Derivative Rules, Power Rule for Differentiation - Calculus
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
Product Rule, Differentiation, Basic Proof, Examples - Calculus
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
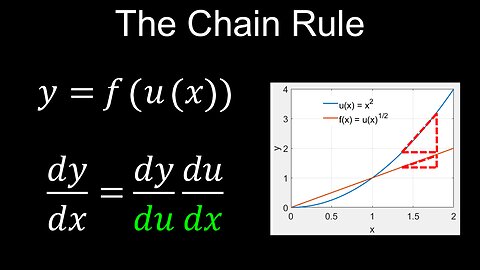
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
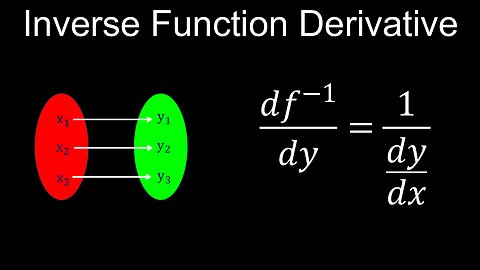
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
Derivatives in Context, Interpretation, Examples - Calculus
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
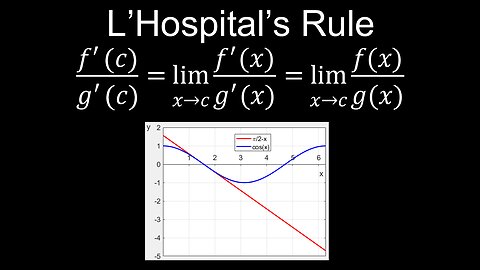
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
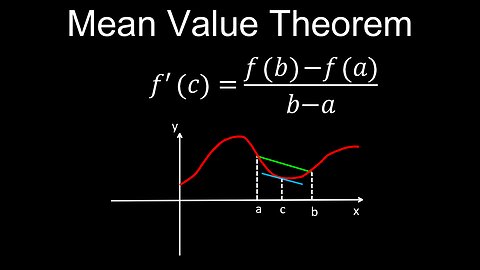
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
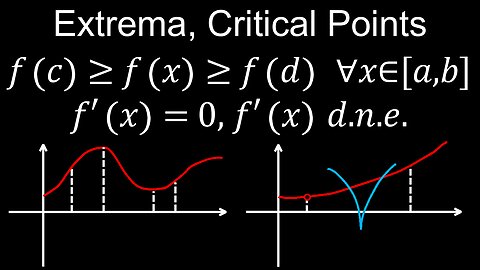
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
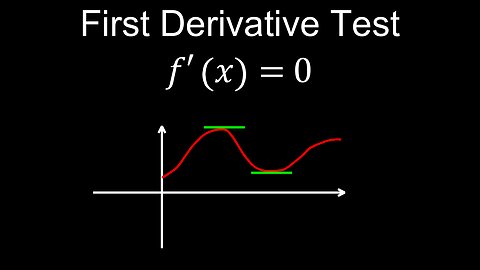
First Derivative Test, Local Extrema, Examples - Calculus
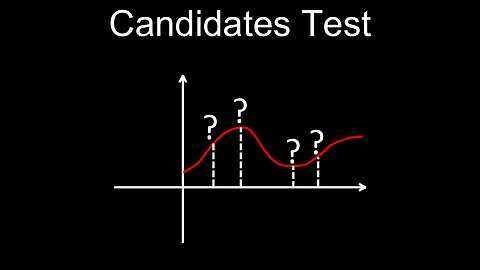
Candidates Test, Global Extrema, Example - Calculus
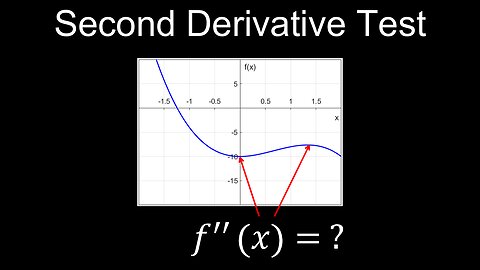
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
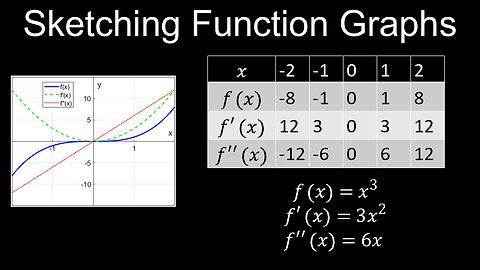
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
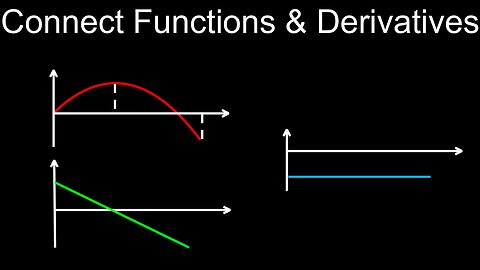
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
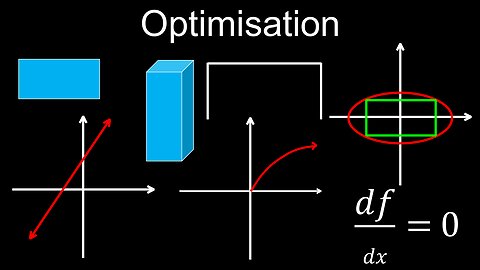
Solving Optimisation Problems, Differentiation, Examples - Calculus
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
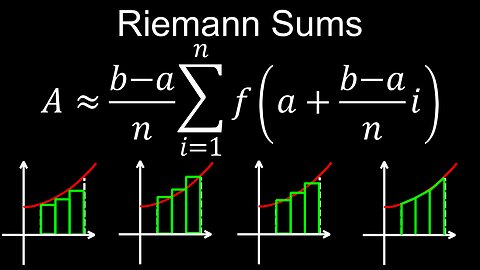
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
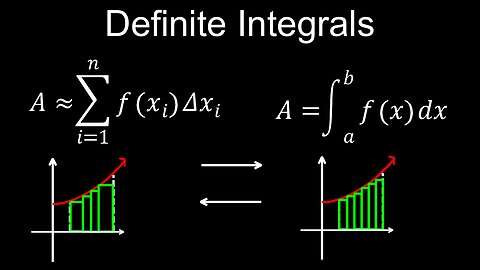
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
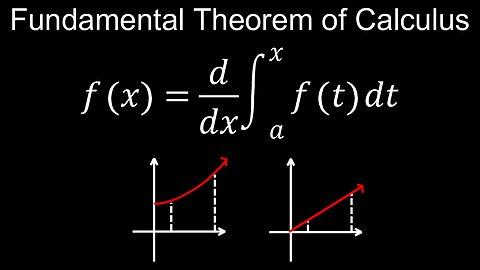
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
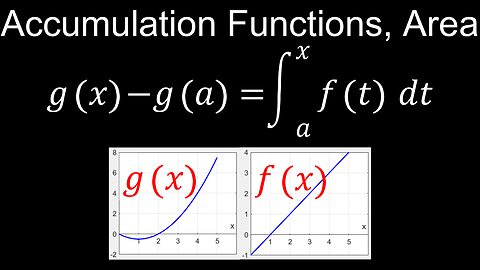
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by Parts, Formula, Rule, Example, Order - Calculus
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
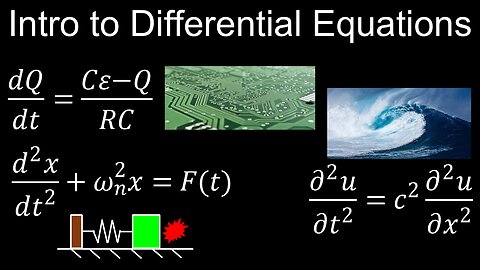
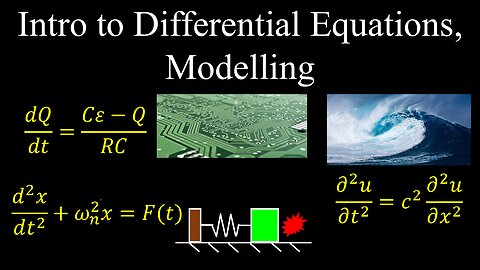
Intro to Differential Equations, Modelling, Worksheet, Example - Calculus
Verifying Solutions to Differential Equations, Examples - Calculus
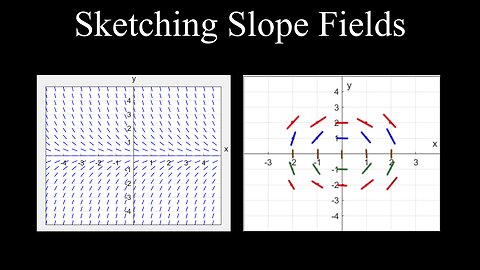
Sketching Slope Fields and Solution Curves Explained, Differential Equations, Example - Calculus
Euler's Method for Solving Differential Equations Explained, Example - Calculus
Intro to Differential Equations, Modelling - Calculus
Verifying Solutions to Differential Equations - Calculus
Sketching Slope Fields, Differential Equations - Calculus
Sketching Solution Curves, Slope Fields - Calculus
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
Separation of Variables, General Solution, ODEs - Calculus
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
Exponential Models, Growth, Decay, Differential Equations - Calculus
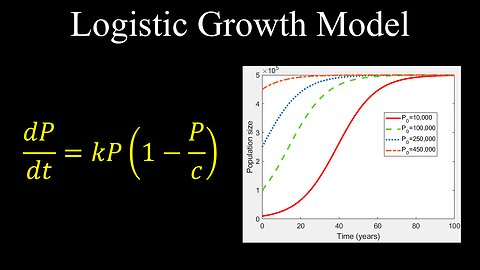
Logistic Growth Model, Differential Equations - Calculus
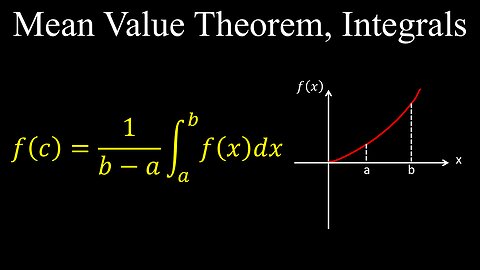
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
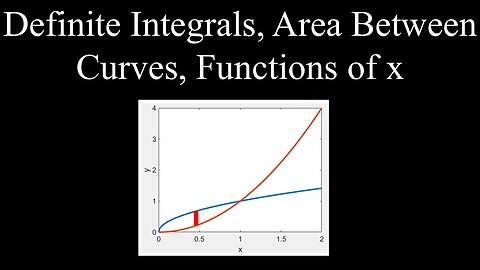
Definite Integrals, Area Between Curves, Functions of x - Calculus
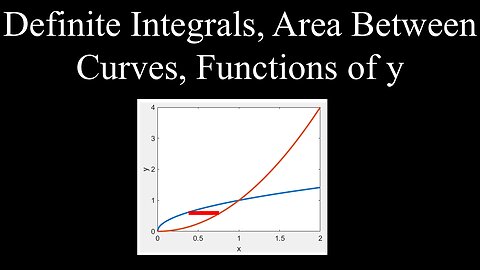
Definite Integrals, Area Between Curves, Functions of y - Calculus
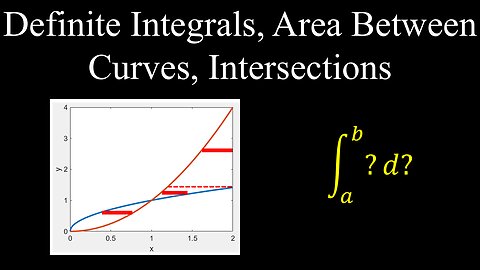
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
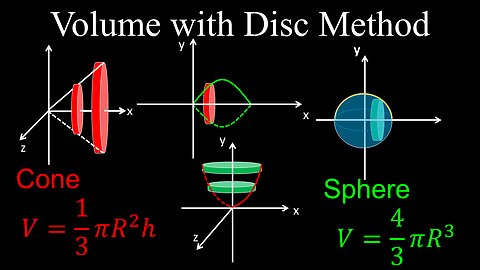
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
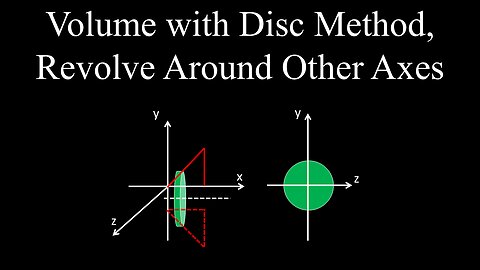
Volume with the Disk Method, Revolving Around other Axes - Calculus
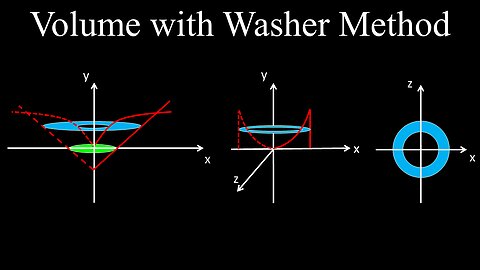
Washer Method to Find the Volume of a Revolved Solid - Calculus
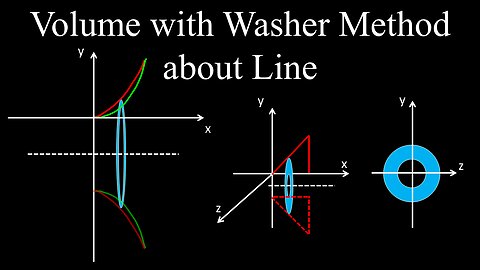
Volume with the Washer Method, Revolved Solid Around Line - Calculus
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
Parametric Equations, Definition, Differentiation - Calculus
Parametric Equations, Second Derivative - Calculus
Parametric Curve, Arc Length, Distance - Calculus
Vector-Valued Functions, Differentiation, Examples - Calculus
Vector-Valued Function, Integration - Calculus
Vector-Valued Functions and Motion in 2D Space - Calculus
Polar Coordinates, Polar Curves, Differentiation - Calculus
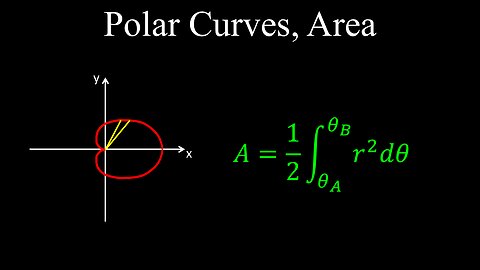
Polar Curve, Area of Region, Integration - Calculus
Polar Curve, Area of Region between Two Curves, Examples - Calculus
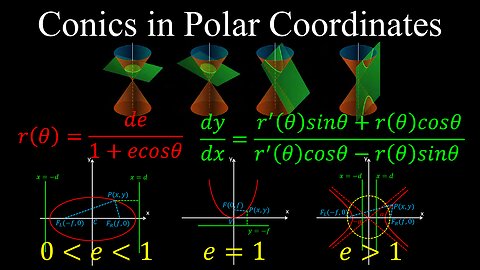
Conics in Polar Coordinates, Derivatives, Example - Calculus
Infinite Sequence, Definition, Representations, Convergence - Calculus
Infinite Series, Definition, Partial Sum, Convergence - Calculus
Geometric Series, Sum, Convergence - Calculus
nth Term Test, Divergence, Infinite Series, Examples - Calculus
Integral Test, Convergence, Infinite Series, Example - Calculus
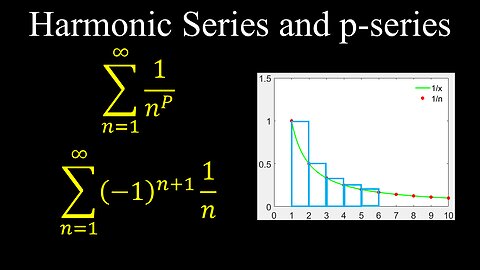
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
Alternating Series Test, Infinite Series - AP Calculus BC
Ratio Test, Infinite Series, Convergence, Examples - Calculus
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
Euler's Method for Solving Differential Equations Explained, Example - Calculus
Euler's method is a simple numerical technique for approximating solutions to first-order ordinary differential equations (ODEs) with an initial value. It works by iteratively moving along the tangent line at each step, using the derivative to find the slope, and advancing the solution by a small step size ('h') to estimate the next point on the solution curve. The basic formula is y₁ = y₀ + h * f(x₀, y₀), where y₀ is the initial value, x₀ is the initial x-value, h is the step size, and f(x₀, y₀) is the slope at the starting point derived from the differential equation.
💡How it Works
• Problem Setup: You start with a differential equation in the form y' = f(x, y) and an initial condition (x₀, y₀).
• Choose a Step Size (h): This is the small increment you'll use to move from one point to the next along the x-axis.
• Calculate the Slope: At the current point (xₙ, yₙ), find the slope using the differential equation: m = f(xₙ, yₙ).
• Estimate the Next Point: Move from the current point by taking a small step of size 'h' along the tangent line. The new y-value is calculated as: yₙ₊₁ = yₙ + h * f(xₙ, yₙ).
• Repeat: Use the new point (xₙ₊₁, yₙ₊₁) as your starting point for the next step and repeat the process to find the next approximation.
💡Key Formula
The core of Euler's method is the iterative formula:
• **yₙ₊₁ = yₙ + h
• f(xₙ, yₙ)**
💡Example Application
Imagine you want to find the approximate value of a solution to y' = 2x and y(1) = 3, using a step size of h = 0.1.
• Initial Condition: (x₀, y₀) = (1, 3).
• Step 1:
⚬ Calculate f(x₀, y₀) = f(1, 3) = 2 * 1 = 2.
⚬ Calculate y₁ = y₀ + h * f(x₀, y₀) = 3 + 0.1 * 2 = 3.2.
• Step 2:
⚬ The new point is (x₁, y₁) = (1 + 0.1, 3.2) = (1.1, 3.2).
⚬ Calculate f(x₁, y₁) = f(1.1, 3.2) = 2 * 1.1 = 2.2.
⚬ Calculate y₂ = y₁ + h * f(x₁, y₁) = 3.2 + 0.1 * 2.2 = 3.42.
You continue this process to find subsequent points.
💡Accuracy and Limitations
• Step Size (h): The accuracy of Euler's method depends on the step size. Smaller step sizes generally lead to better approximations but require more computational steps.
• First-Order Method: It is a first-order method, meaning it assumes the slope remains constant over the small interval, which introduces some error.
• Applications: Despite its limitations, Euler's method is fundamental in computational science and forms the basis for more complex numerical methods used to solve and simulate differential equations in fields like engineering and physics.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DMK4EA0f8SfF4SgdiOZ39F73He_YWIwe/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1QpzjiCPjfoxydzZqvjyJJsqv9jyRLZ0o/view?usp=drive_link
💡Chapters:
00:00 Euler's method
01:23 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 2:13:33
2:13:33
Side Scrollers Podcast
4 hours agoAsmongold SUED for Emotional Distress + Hasan REJECTED+ INSANE Plane Crash + More | Side Scrollers
38.6K11 -
 1:00:32
1:00:32
VINCE
7 hours agoNYC Has Been Seized By The Communists | Episode 162 - 11/05/25
255K384 -
 1:47:26
1:47:26
LadyDesireeMusic
4 hours agoLive Piano & Convo Rumble Rants/ Subs to Request
28.1K3 -
 5:02:14
5:02:14
SOLTEKGG
5 hours agoGOING FOR KILL RECORD - BF6 SKIN Giveaway
21.1K1 -
 1:04:48
1:04:48
The Rubin Report
5 hours agoCharlie Kirk’s Warning for MAGA if Mamdani Won
53.1K202 -
 1:33:32
1:33:32
Graham Allen
7 hours agoTold You The War Was FAR From Over… The Blue Wave Just Proved It! Evil Is Fighting Back!
133K110 -
 2:54:17
2:54:17
Badlands Media
13 hours agoBadlands Daily: November 5, 2025 – Election Illusions, Filibuster Fallout & The Deep State’s Next Move
119K25 -
 3:01:00
3:01:00
Wendy Bell Radio
11 hours agoLike Sheep To Slaughter
141K129 -
 1:13:30
1:13:30
DML
6 hours agoDML LIVE: NYC Goes Socialist: Mamdani’s Victory
88.2K41 -
 1:04:43
1:04:43
Chad Prather
19 hours agoTruth on Trial: When Fear Meets Faith
105K56