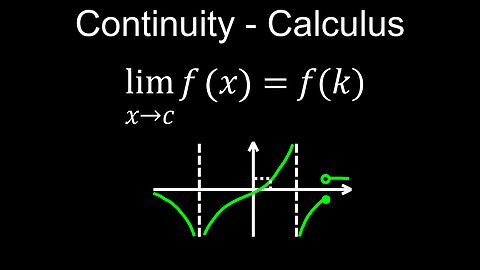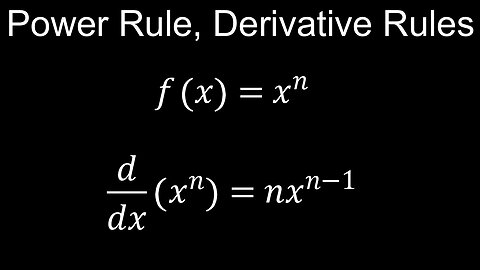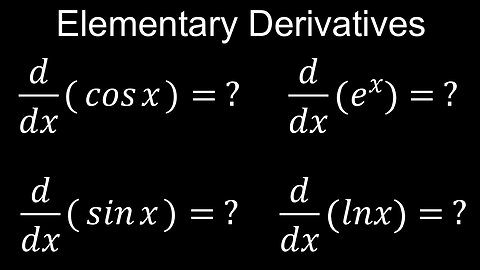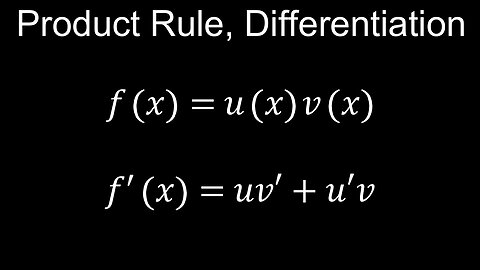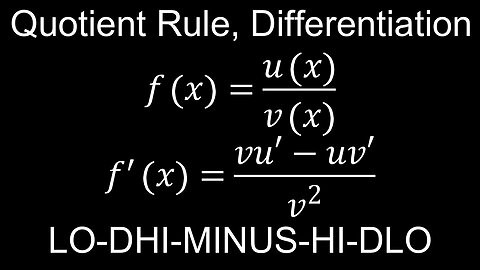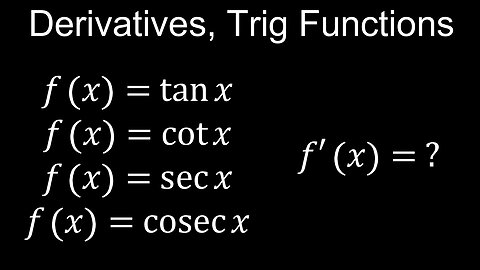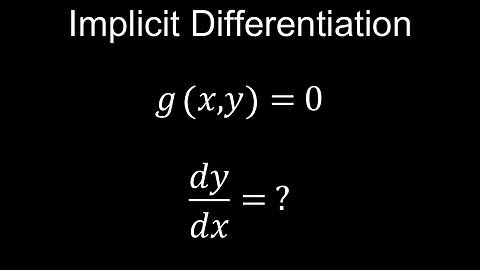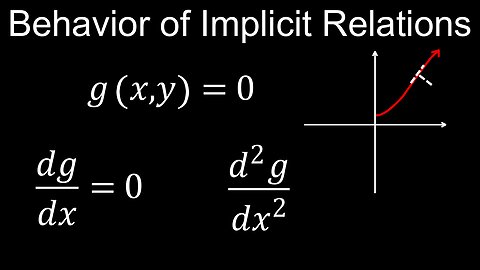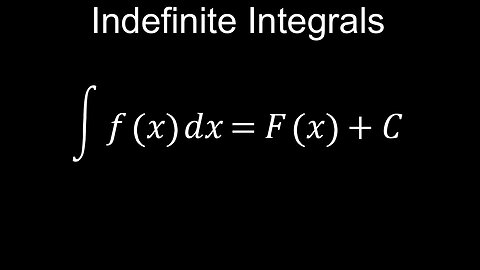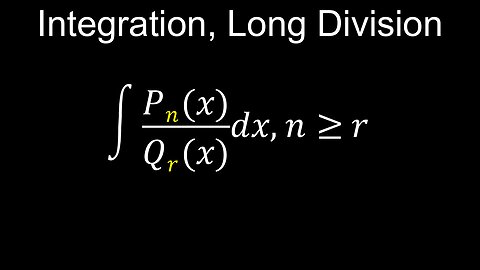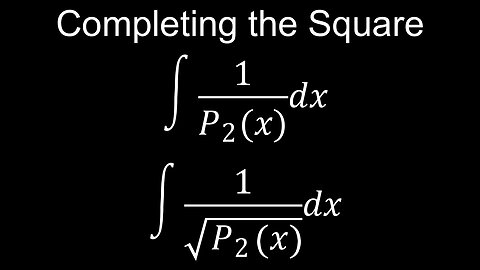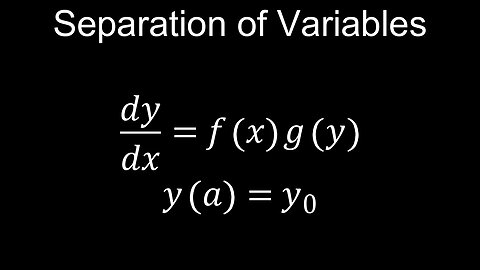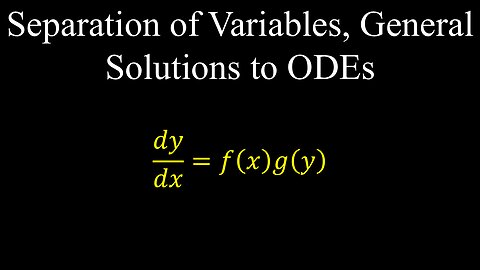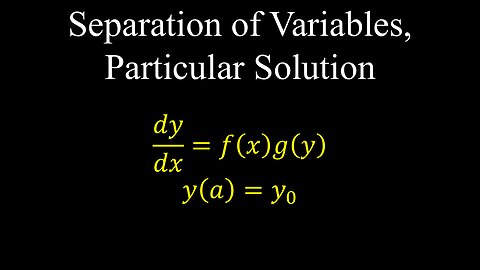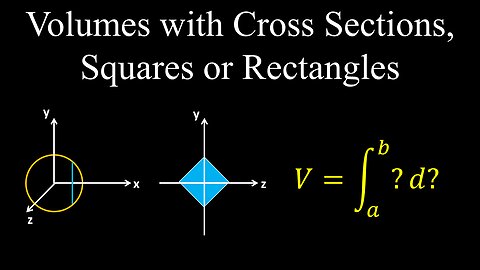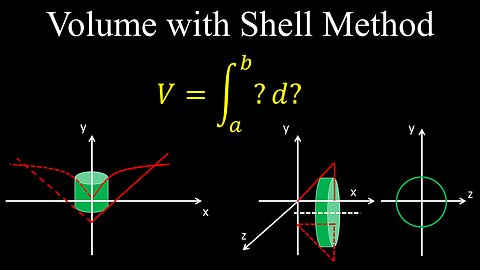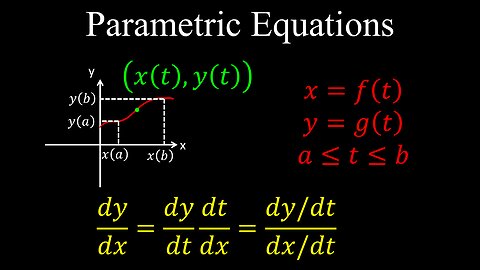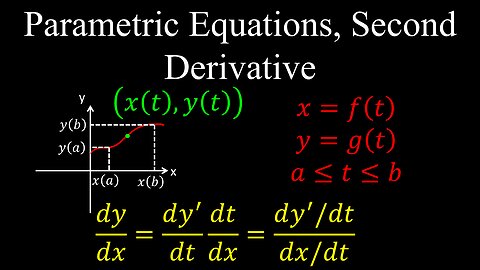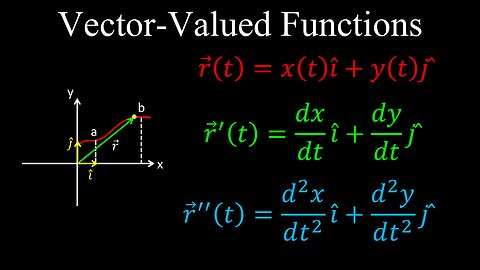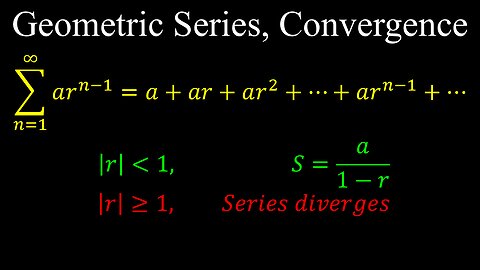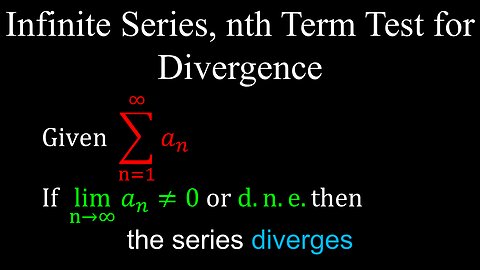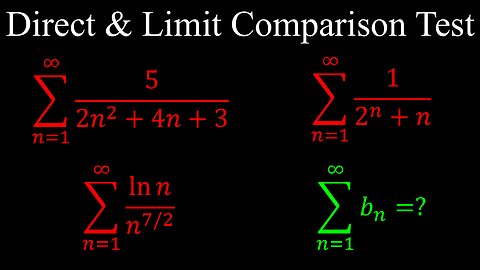Premium Only Content
Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
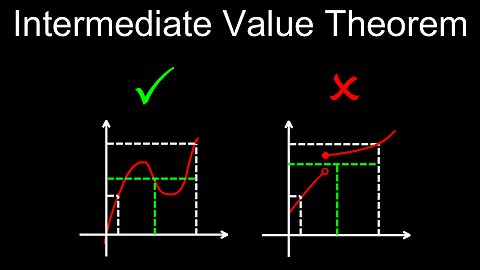
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
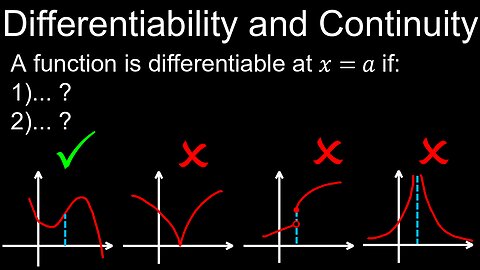
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
Derivative Rules, Power Rule for Differentiation - Calculus
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
Product Rule, Differentiation, Basic Proof, Examples - Calculus
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
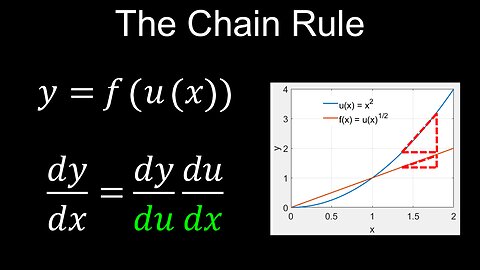
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
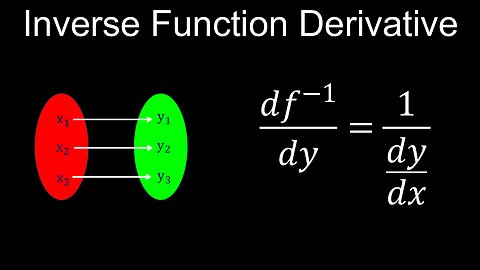
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
Derivatives in Context, Interpretation, Examples - Calculus
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
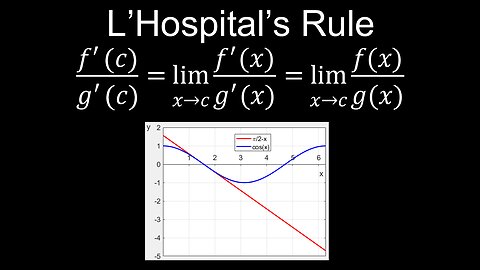
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
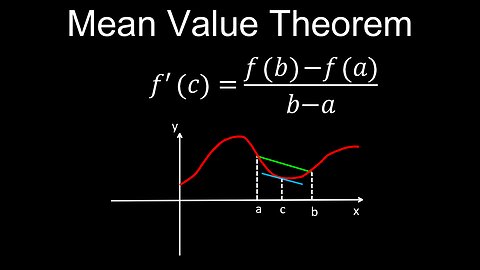
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
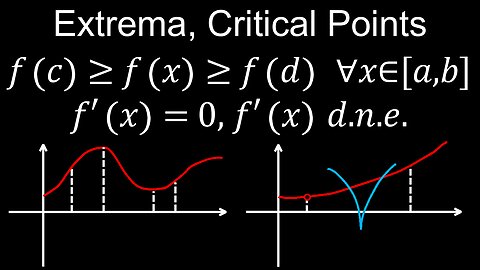
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
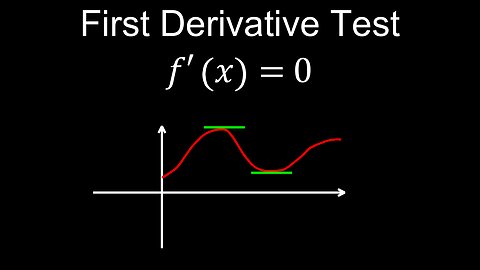
First Derivative Test, Local Extrema, Examples - Calculus
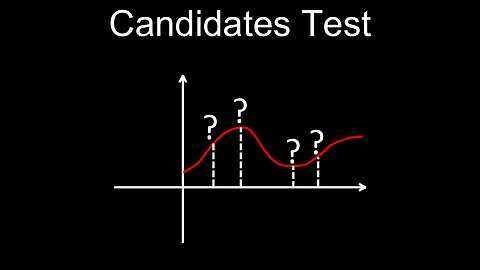
Candidates Test, Global Extrema, Example - Calculus
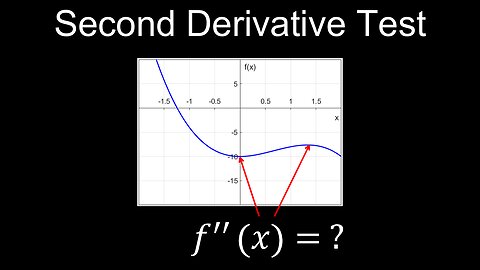
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
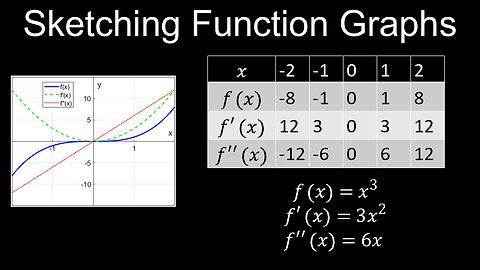
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
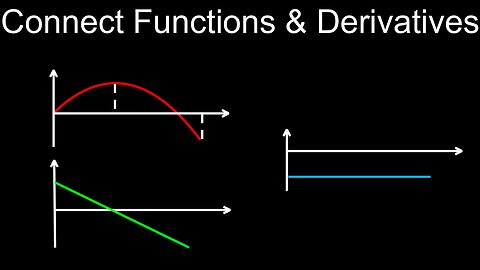
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
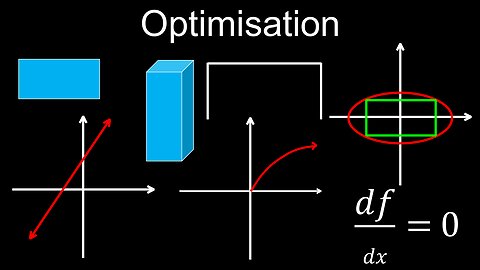
Solving Optimisation Problems, Differentiation, Examples - Calculus
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
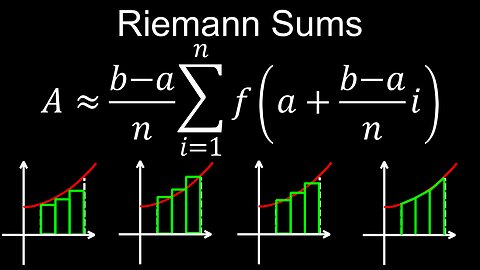
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
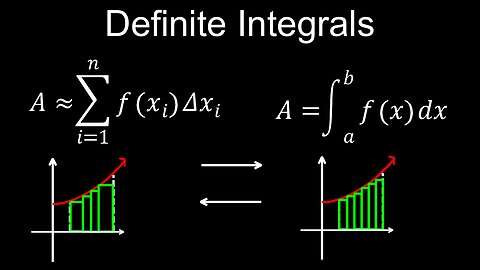
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
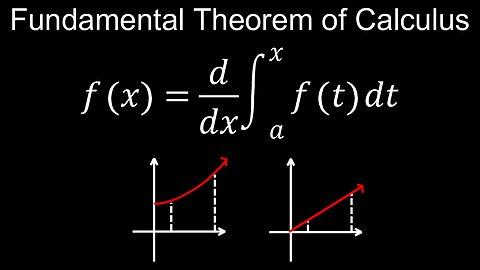
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
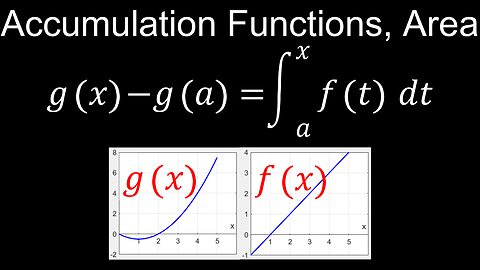
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by Parts, Formula, Rule, Example, Order - Calculus
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
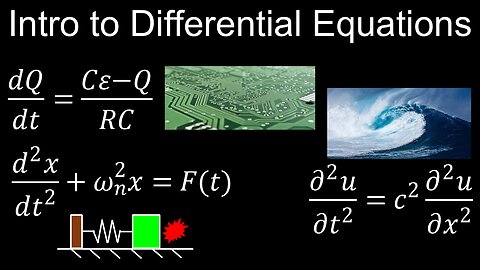
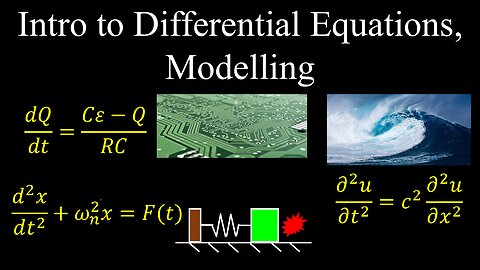
Intro to Differential Equations, Modelling, Worksheet, Example - Calculus
Verifying Solutions to Differential Equations, Examples - Calculus
Sketching Slope Fields and Solution Curves Explained, Differential Equations, Example - Calculus
Euler's Method for Solving Differential Equations Explained, Example - Calculus
Separation of Variables Method, Differential Equations, Integration, Examples - Calculus
Exponential Models with Differential Equations, Population Growth, Examples - Calculus
Logistic Growth Differential Equation, Model, Example - Calculus
Intro to Differential Equations, Modelling - Calculus
Verifying Solutions to Differential Equations - Calculus
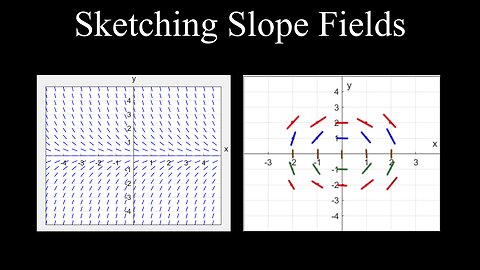
Sketching Slope Fields, Differential Equations - Calculus
Sketching Solution Curves, Slope Fields - Calculus
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
Separation of Variables, General Solution, ODEs - Calculus
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
Exponential Models, Growth, Decay, Differential Equations - Calculus
Logistic Growth Model, Differential Equations - Calculus
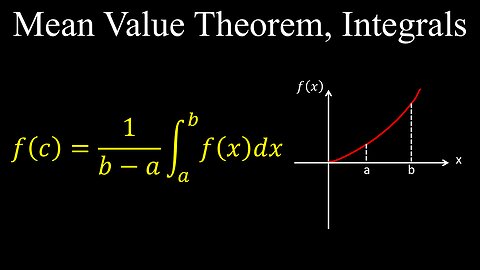
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
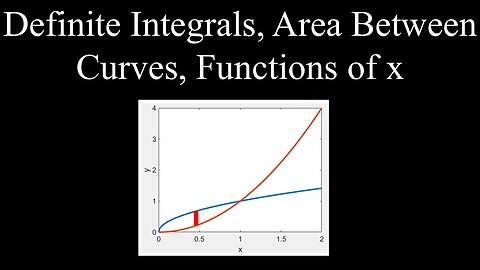
Definite Integrals, Area Between Curves, Functions of x - Calculus
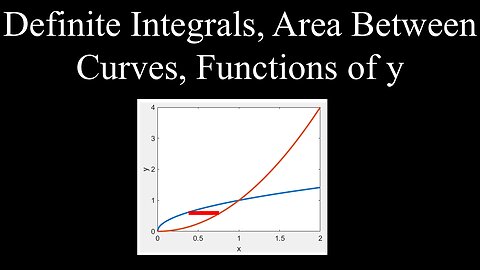
Definite Integrals, Area Between Curves, Functions of y - Calculus
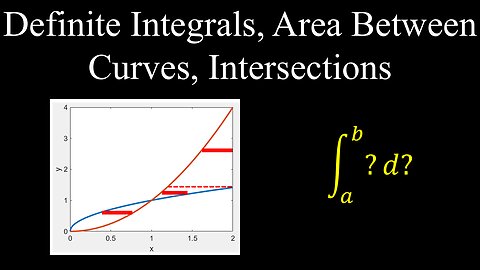
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
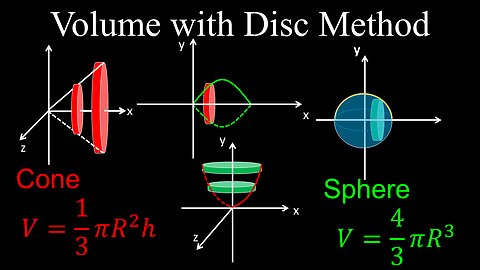
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
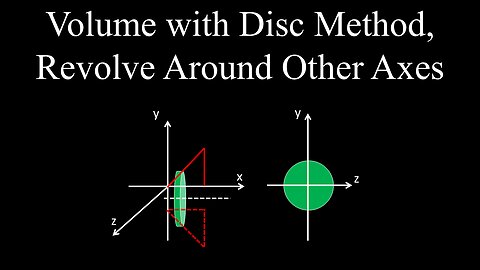
Volume with the Disk Method, Revolving Around other Axes - Calculus
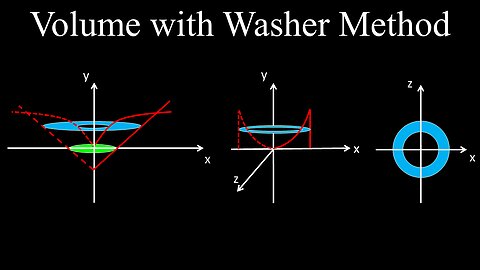
Washer Method to Find the Volume of a Revolved Solid - Calculus
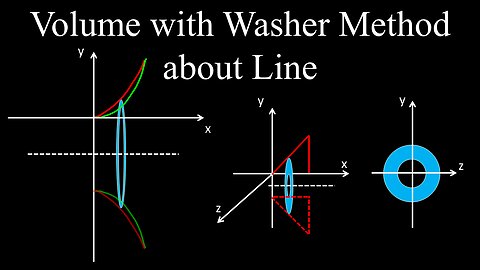
Volume with the Washer Method, Revolved Solid Around Line - Calculus
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
Parametric Equations, Definition, Differentiation - Calculus
Parametric Equations, Second Derivative - Calculus
Parametric Curve, Arc Length, Distance - Calculus
Vector-Valued Functions, Differentiation, Examples - Calculus
Vector-Valued Function, Integration - Calculus
Vector-Valued Functions and Motion in 2D Space - Calculus
Polar Coordinates, Polar Curves, Differentiation - Calculus
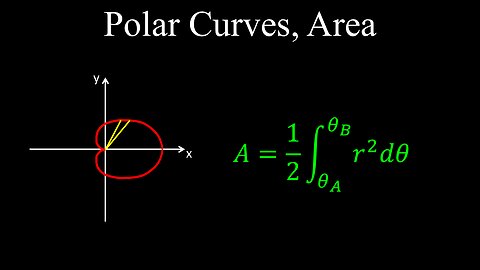
Polar Curve, Area of Region, Integration - Calculus
Polar Curve, Area of Region between Two Curves, Examples - Calculus
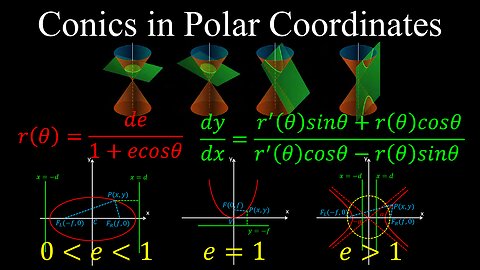
Conics in Polar Coordinates, Derivatives, Example - Calculus
Infinite Sequence, Definition, Representations, Convergence - Calculus
Infinite Series, Definition, Partial Sum, Convergence - Calculus
Geometric Series, Sum, Convergence - Calculus
nth Term Test, Divergence, Infinite Series, Examples - Calculus
Integral Test, Convergence, Infinite Series, Example - Calculus
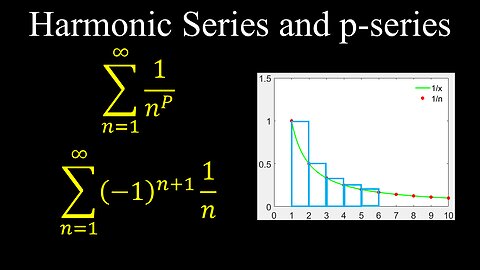
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
Alternating Series Test, Infinite Series - AP Calculus BC
Ratio Test, Infinite Series, Convergence, Examples - Calculus
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
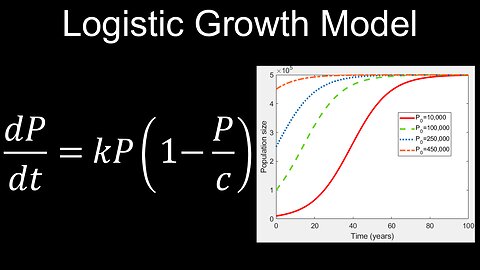
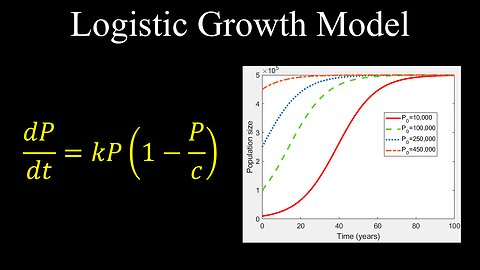
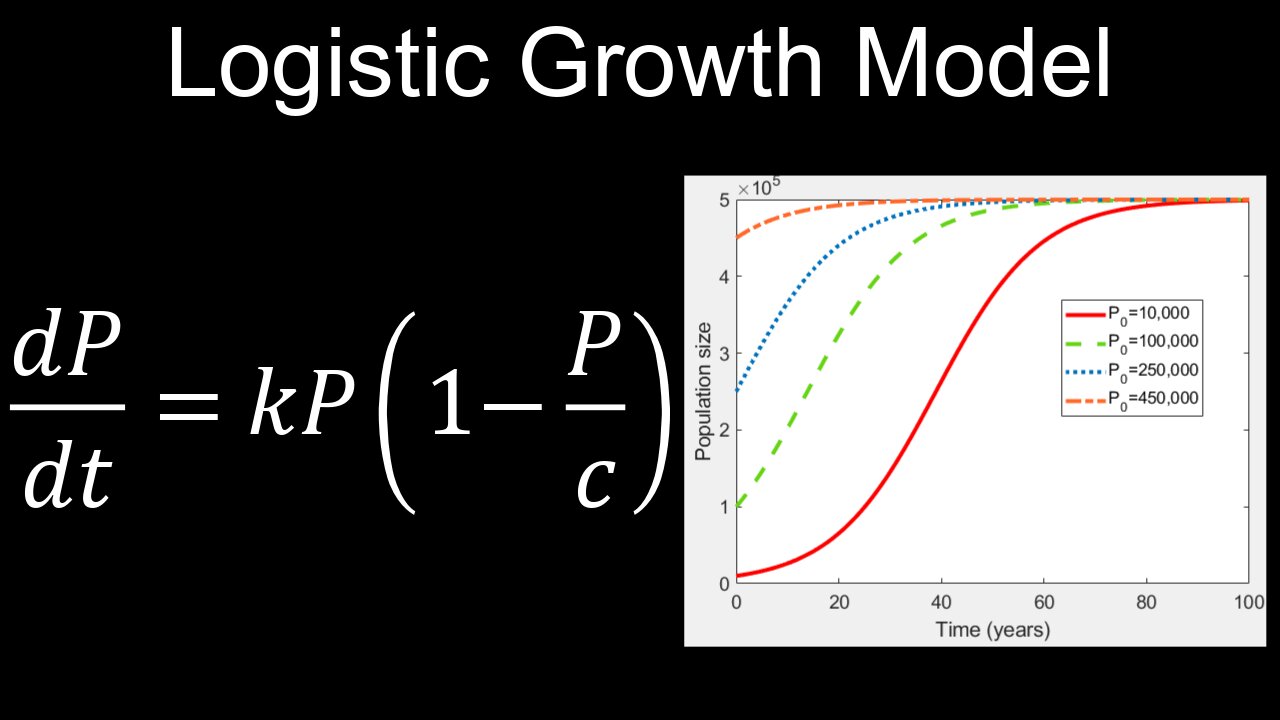
Logistic Growth Differential Equation, Model, Example - Calculus
The logistic growth differential equation is represented as dP/dt = rP(1 - P/K), where P is the population, t is time, r is the growth rate, and K is the carrying capacity, which represents the maximum population an environment can sustain. This equation models how a population's growth slows down as it approaches the carrying capacity, providing a more realistic model than simple exponential growth.
💡Components of the Equation
• dP/dt: The rate of change of the population with respect to time.
• P: The population size at any given time t.
• r: The intrinsic growth rate, which determines how quickly the population would grow without environmental limitations.
• K: The carrying capacity, the maximum population size the environment can sustainably support.
💡How the Equation Works
• When P is small: The term (1 - P/K) is close to 1, so dP/dt ≈ rP, resembling exponential growth.
• As P approaches K: The term (1 - P/K) becomes smaller, reducing the growth rate dP/dt.
• When P = K: The term (1 - P/K) becomes 0, and dP/dt = 0, indicating that the population has stabilized at the carrying capacity.
This model contrasts with exponential growth, where the growth rate continuously increases with the population size. The logistic equation accounts for limited resources, ensuring that the population growth eventually levels off.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DMK4EA0f8SfF4SgdiOZ39F73He_YWIwe/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1QpzjiCPjfoxydzZqvjyJJsqv9jyRLZ0o/view?usp=drive_link
💡Chapters:
00:00 Logistic growth model
01:15 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 18:03
18:03
Nikko Ortiz
1 day agoEBT Meltdowns Are Insane...
27.5K58 -
 17:33
17:33
a12cat34dog
1 day agoRUMBLE TAKEOVER @ DREAMHACK | VLOG | {HALLOWEEN 2025}
56.5K25 -
 10:48
10:48
GritsGG
18 hours agoWarzone Stadium Easter Egg! Unlock Grau Blueprint EASY!
32.1K2 -
 LIVE
LIVE
Lofi Girl
3 years agolofi hip hop radio 📚 - beats to relax/study to
481 watching -
 1:43:54
1:43:54
TruthStream with Joe and Scott
3 days agoStuey and Elisa V interview Joe and Scott Q, AI, Glutathione, Tylenol etc 11/5 #510
30.6K6 -
 29:15
29:15
BlabberingCollector
2 days agoHarry Potter X Fortnite, Fans Reee Over Trans Rights, NEW Audiobooks Are OUT, Wizarding Quick Hits
42.5K4 -
 1:20:42
1:20:42
The Connect: With Johnny Mitchell
6 days ago $24.12 earnedThe Truth Behind The U.S. Invasion Of Venezuela: Ed Calderon Exposes American Regime Change Secrets
56.8K33 -
 2:10:18
2:10:18
FreshandFit
10 hours agoAfter Hours w/ Girls
147K52 -
 2:06:29
2:06:29
TimcastIRL
16 hours agoAirlines Cancel Over 700 Flights, Travel APOCALYPSE Is Now, Trump Says END FILIBUSTER | Timcast IRL
249K148 -
 9:02:44
9:02:44
SpartakusLIVE
21 hours agoTOXIC Solos on ARC Raiders || Friday Night HYPE - WZ or Redsec Later?
83K2