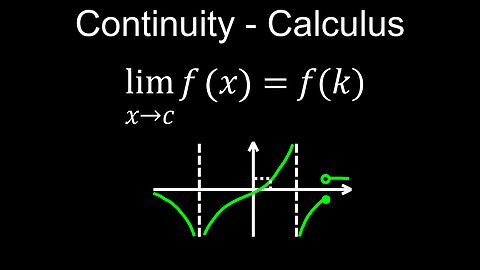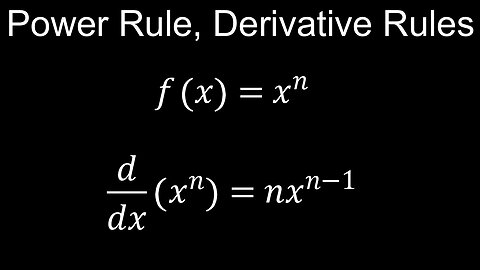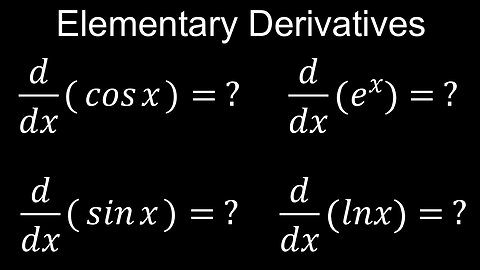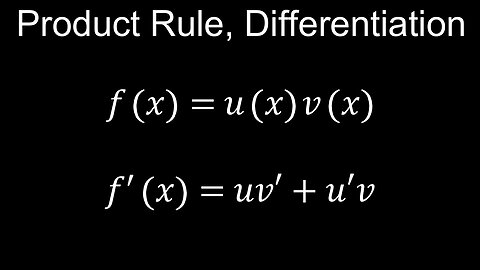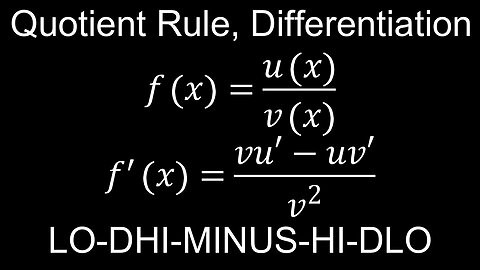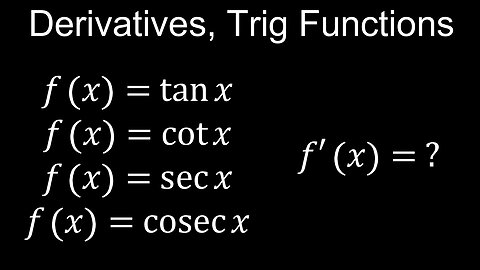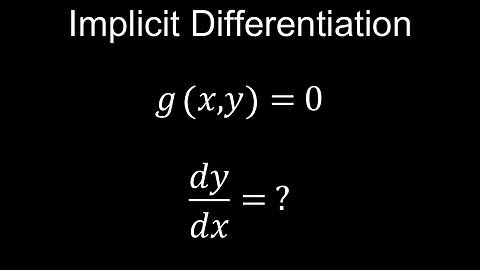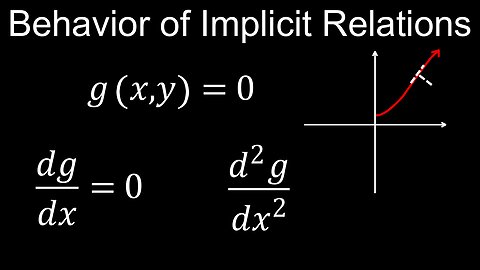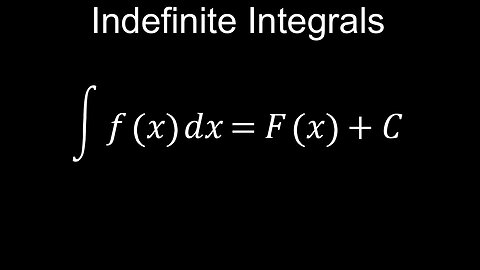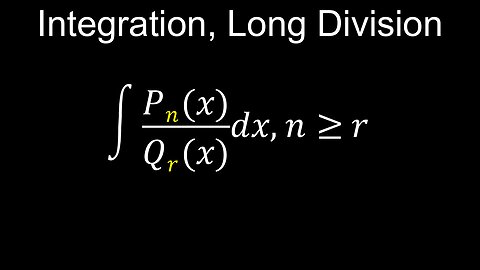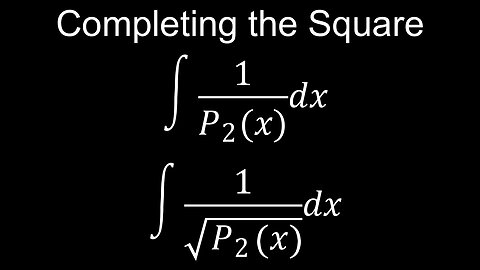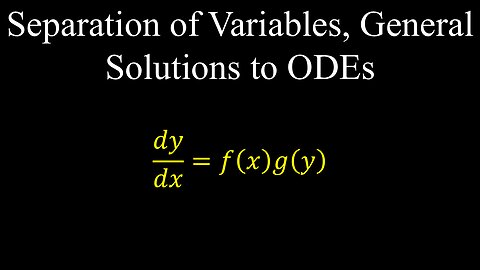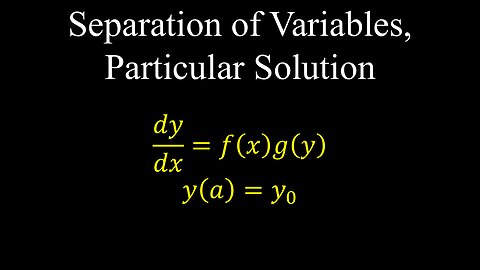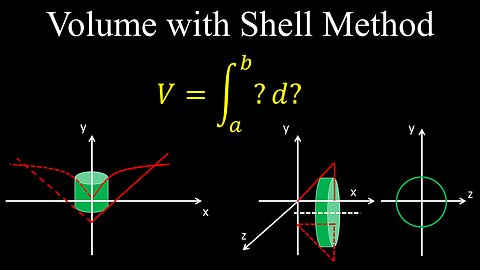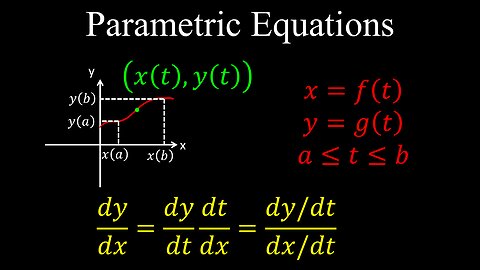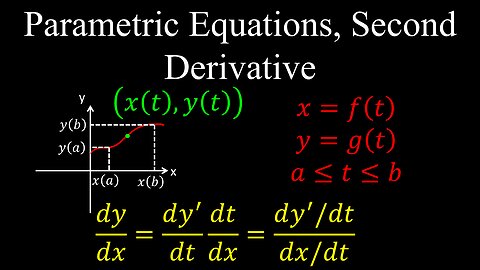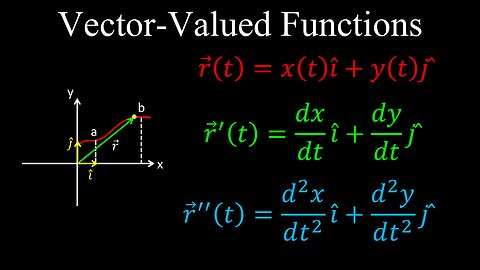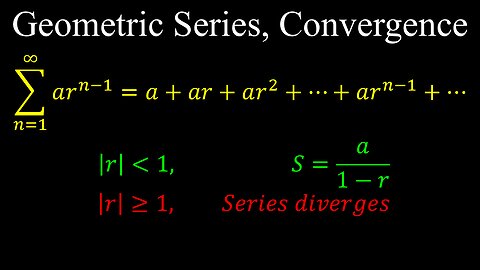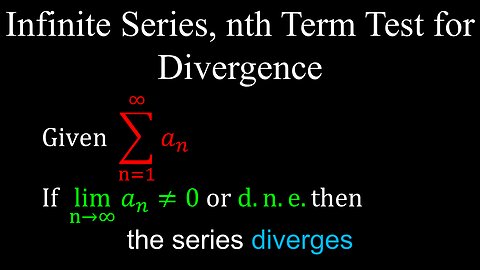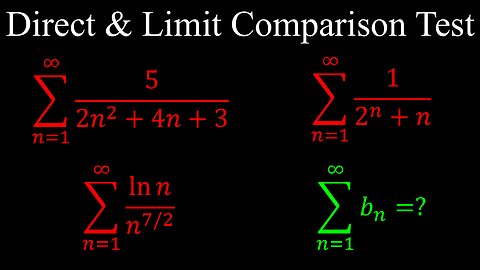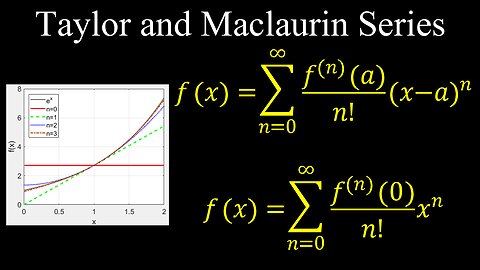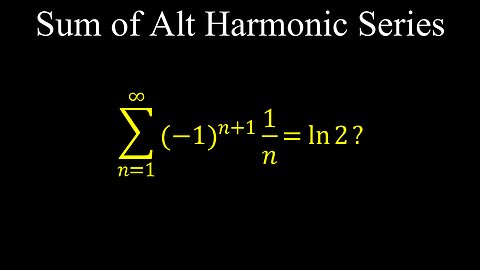Premium Only Content
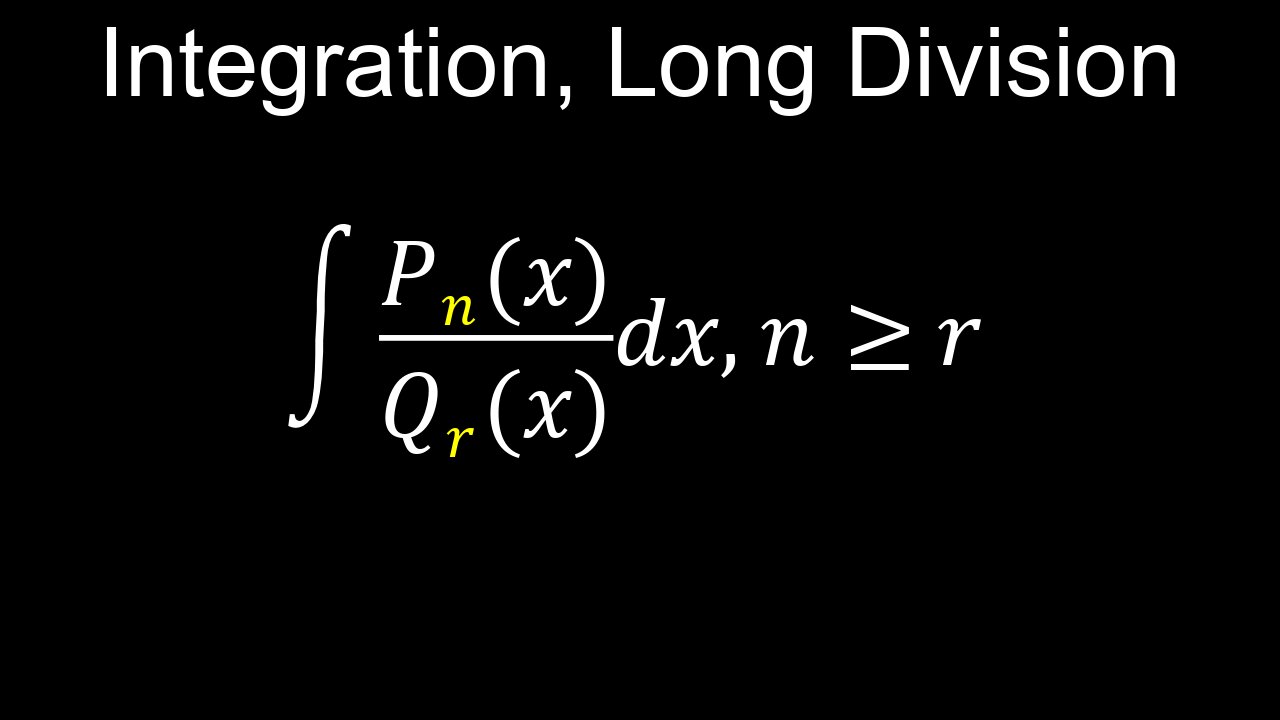
Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
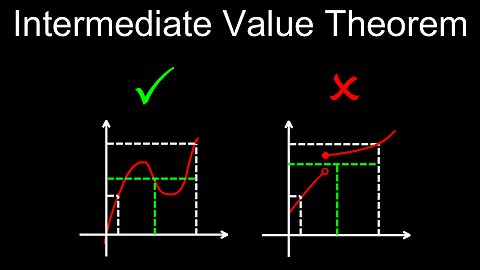
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
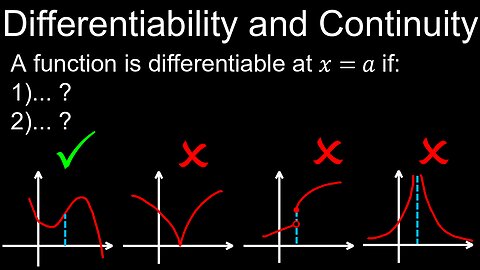
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
Derivative Rules, Power Rule for Differentiation - Calculus
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
Product Rule, Differentiation, Basic Proof, Examples - Calculus
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
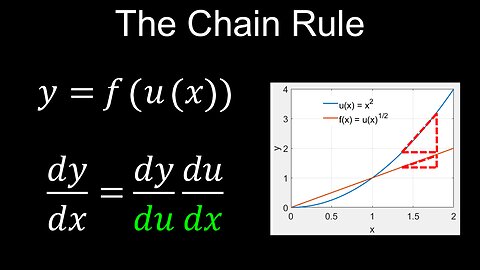
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
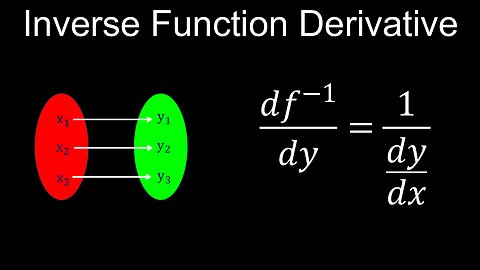
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
Derivatives in Context, Interpretation, Examples - Calculus
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
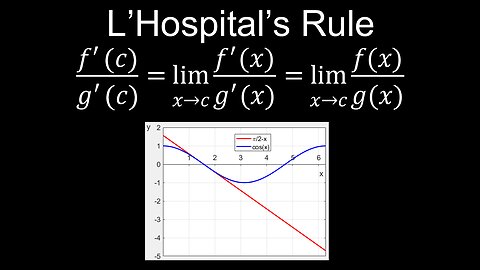
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
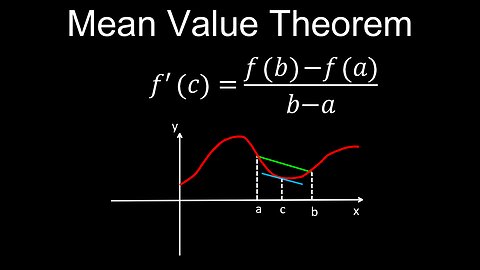
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
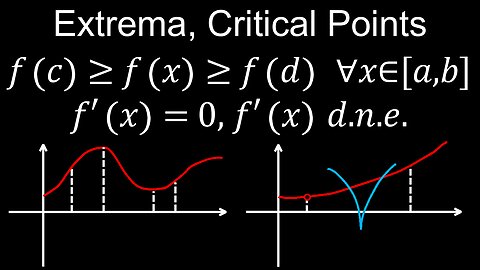
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
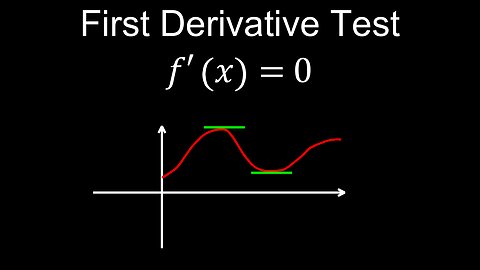
First Derivative Test, Local Extrema, Examples - Calculus
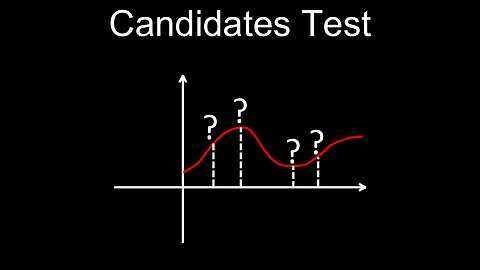
Candidates Test, Global Extrema, Example - Calculus
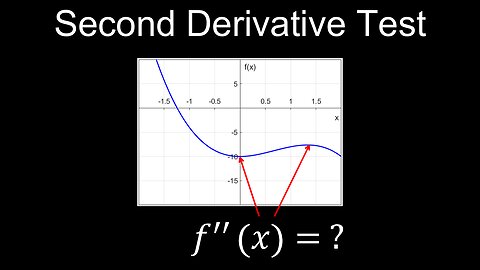
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
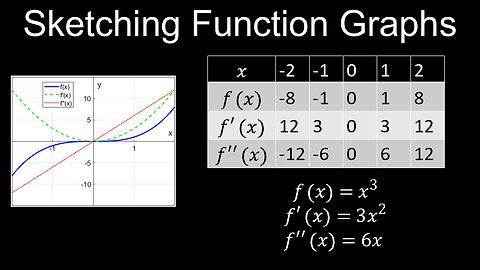
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
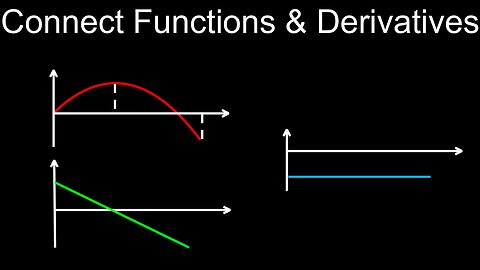
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
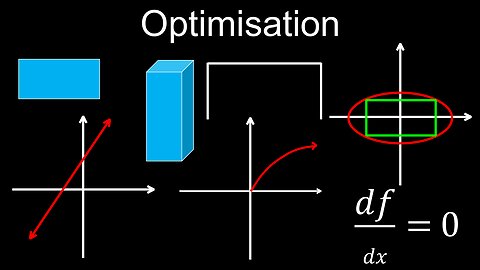
Solving Optimisation Problems, Differentiation, Examples - Calculus
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
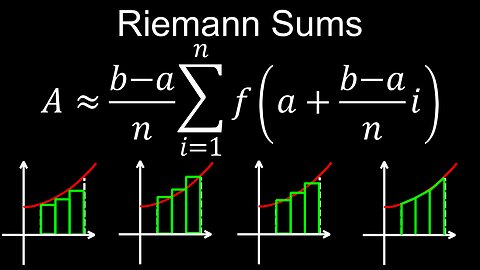
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
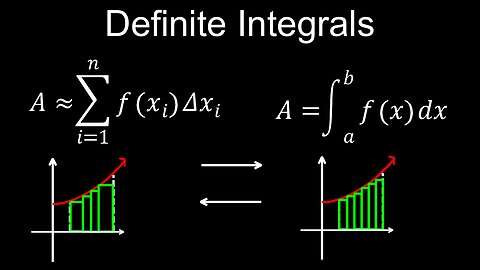
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
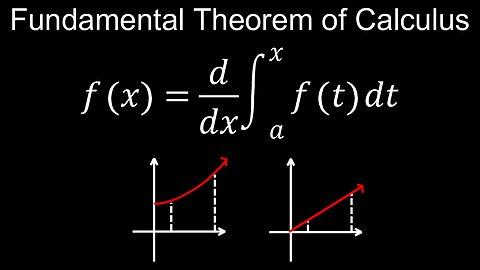
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
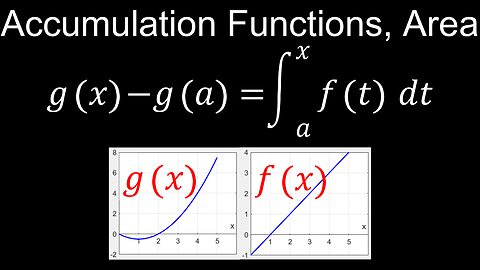
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by Parts, Formula, Rule, Example, Order - Calculus
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
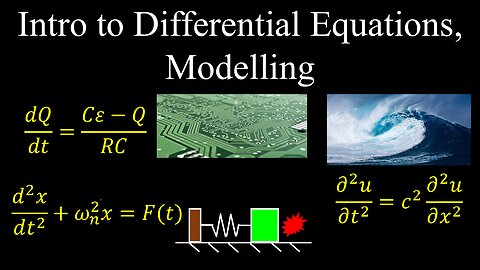
Intro to Differential Equations, Modelling - Calculus
Verifying Solutions to Differential Equations - Calculus
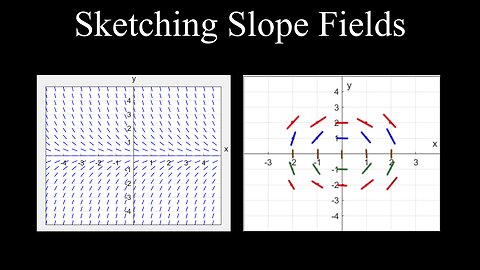
Sketching Slope Fields, Differential Equations - Calculus
Sketching Solution Curves, Slope Fields - Calculus
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
Separation of Variables, General Solution, ODEs - Calculus
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
Exponential Models, Growth, Decay, Differential Equations - Calculus
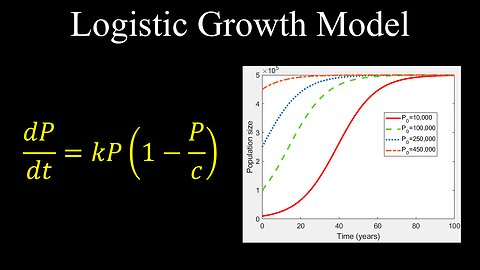
Logistic Growth Model, Differential Equations - Calculus
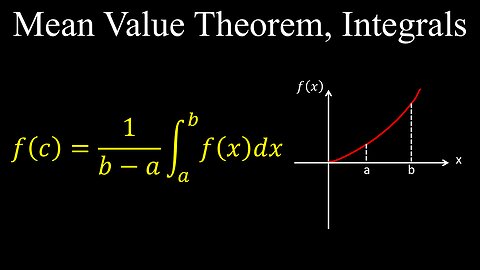
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
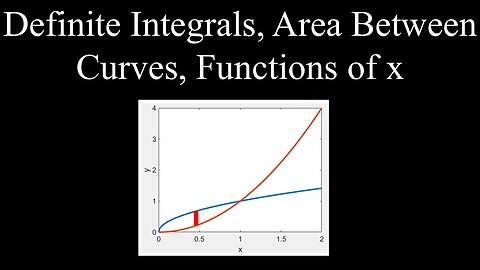
Definite Integrals, Area Between Curves, Functions of x - Calculus
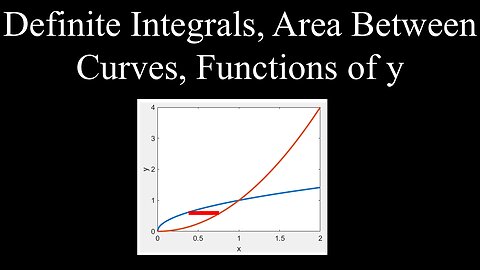
Definite Integrals, Area Between Curves, Functions of y - Calculus
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
Volume with the Disk Method, Revolving Around other Axes - Calculus
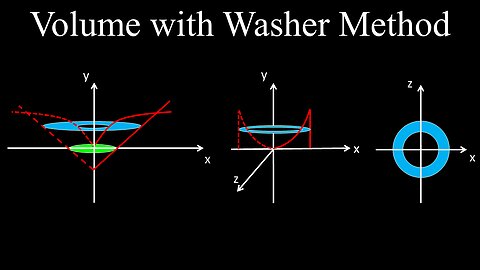
Washer Method to Find the Volume of a Revolved Solid - Calculus
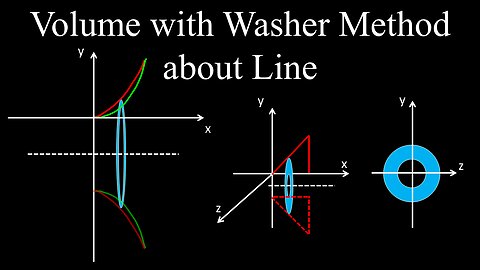
Volume with the Washer Method, Revolved Solid Around Line - Calculus
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
Parametric Equations, Definition, Differentiation - Calculus
Parametric Equations, Second Derivative - Calculus
Parametric Curve, Arc Length, Distance - Calculus
Vector-Valued Functions, Differentiation, Examples - Calculus
Vector-Valued Function, Integration - Calculus
Vector-Valued Functions and Motion in 2D Space - Calculus
Polar Coordinates, Polar Curves, Differentiation - Calculus
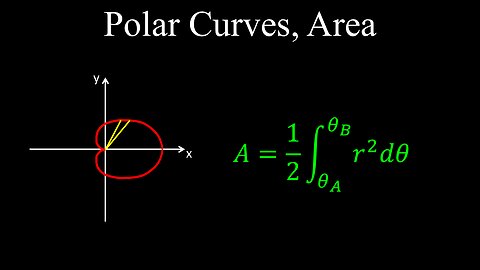
Polar Curve, Area of Region, Integration - Calculus
Polar Curve, Area of Region between Two Curves, Examples - Calculus
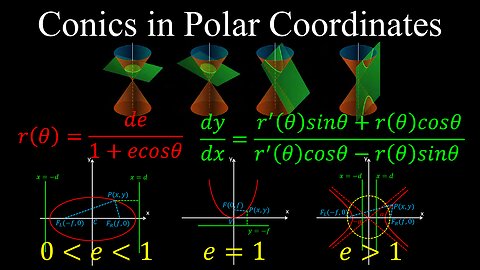
Conics in Polar Coordinates, Derivatives, Example - Calculus
Infinite Sequence, Definition, Representations, Convergence - Calculus
Infinite Series, Definition, Partial Sum, Convergence - Calculus
Geometric Series, Sum, Convergence - Calculus
nth Term Test, Divergence, Infinite Series, Examples - Calculus
Integral Test, Convergence, Infinite Series, Example - Calculus
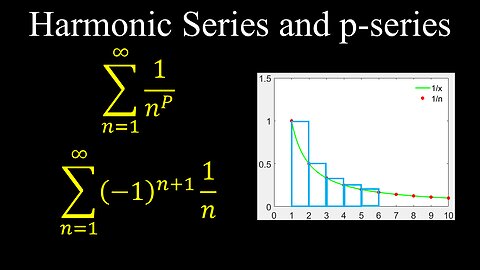
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
Alternating Series Test, Infinite Series - AP Calculus BC
Ratio Test, Infinite Series, Convergence, Examples - Calculus
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
Alternating Series, Error Bound - Calculus
Taylor Polynomials, Approximating Functions - Calculus
Lagrange Error Bound, Taylor Polynomials - Calculus
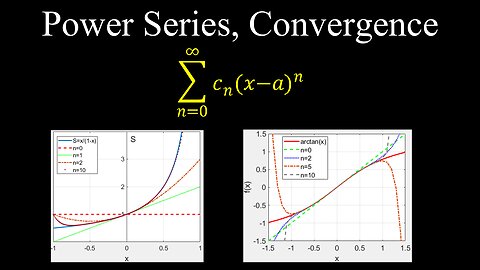
Power Series, Convergence - Calculus
Taylor Series, Maclaurin Series - Calculus
Representing Functions as Power Series - Calculus
Sum of Alternating Harmonic Series (-1)^(n+1)1/n = ln2 - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration using long division is a technique to integrate improper rational functions, where the degree of the numerator is greater than or equal to the degree of the denominator. The process involves performing polynomial long division to rewrite the integrand as a polynomial plus a proper rational function (where the numerator's degree is less than the denominator's). The polynomial part is integrated directly using basic rules, while the proper rational function part is then integrated using other methods, such as partial fraction decomposition or completing the square.
💡When to Use Long Division for Integration
• Improper Rational Functions: Use this method when you're faced with an integral containing a rational expression (a fraction of polynomials) where the numerator's degree is greater than or equal to the denominator's degree.
💡Steps for Integration Using Long Division
• Perform Long Division: Divide the numerator by the denominator to find the quotient and remainder.
• Rewrite the Integrand: Express the original rational function as the quotient plus the remainder divided by the divisor.
∘ Original integrand = Quotient + (Remainder / Divisor)
• Integrate Term by Term: The integral can now be broken down into the integral of the polynomial (quotient) and the integral of the proper rational function (remainder/divisor).
∘ ∫ (Numerator/Denominator) dx = ∫ (Quotient) dx + ∫ (Remainder/Divisor) dx
• Integrate the Polynomial: The integral of the polynomial quotient is found using the power rule for integration.
• Integrate the Proper Rational Function: The remaining integral, which is now a proper rational function, can be integrated using techniques like:
• Partial Fraction Decomposition: If the denominator can be factored into simpler linear or irreducible quadratic factors.
• Completing the Square: If the denominator is an irreducible quadratic, completing the square can transform it into a form suitable for arctangent integrals or logarithmic forms.
• U-Substitution: U-substitution might be used to simplify the integral of the proper rational piece.
💡Example
To integrate ∫ (x³ + 3x² + 8x + 19) / (x² + 5) dx, you would first perform long division.
• Long Division: Divide x³ + 3x² + 8x + 19 by x² + 5, yielding a quotient of (x + 3) and a remainder of (3x + 4).
• Rewrite: The integral becomes ∫ (x + 3 + (3x + 4)/(x² + 5)) dx.
• Integrate:
∘∫ (x + 3) dx = x²/2 + 3x
∘∫ (3x / (x² + 5)) dx + ∫ (4 / (x² + 5)) dx
∘These remaining integrals are solved using u-substitution and arctangent integration, respectively, resulting in (3/2)ln(x² + 5) and (4/√5)arctan(x/√5).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Integration by polynomial long division
01:02 Worked Example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 1:10:12
1:10:12
The Quartering
3 hours agoFood Wars Begin! Terror Plot Foiled & Much More!
61.9K20 -
 1:09:50
1:09:50
The Culture War with Tim Pool
4 hours agoJamaica Hurricane Predicts POLE SHIFT, The END Is Nigh | The Culture War with Tim Pool
110K93 -
 2:44:08
2:44:08
Lara Logan
10 hours agoSHOTS FIRED: The Tyranny of Big Pharma Exposed with Dr. Sherri Tenpenny | EP 42 | Lara Logan
22K6 -
 1:01:45
1:01:45
Playback Request Live
1 hour agoPRL LIVE @ DREAMHACK!!
10.3K1 -
 LIVE
LIVE
Dr Disrespect
5 hours ago🔴LIVE - DR DISRESPECT - ARC RAIDERS - DANGEROUS ADVENTURES (LEVEL 12)
1,394 watching -
 14:15
14:15
Tactical Advisor
5 days agoEverything You Need To Know About PSA Mixtape Vol 1. (FIRST LOOK)
2.82K3 -
 LIVE
LIVE
Jeff Ahern
1 hour agoFriday Freak out with Jeff Ahern
104 watching -
 14:54
14:54
The Kevin Trudeau Show Limitless
2 days agoThe Hidden Force Running Your Life
54.4K8 -
 1:03:55
1:03:55
Sean Unpaved
3 hours agoRavens' Resurrection Night: Lamar Buries Miami, NFL/CFB Spooky HC Shifts, & Kalshi's Week 9/10 Odds!
26.5K -
 2:16:48
2:16:48
Film Threat
1 day agoHALLOWEEN HORROR + BACK TO THE FUTURE RERELEASE + MORE REVIEWS | Film Threat Livecast
16.4K