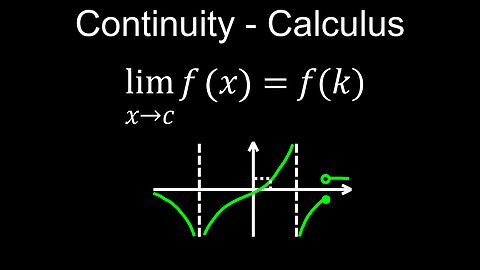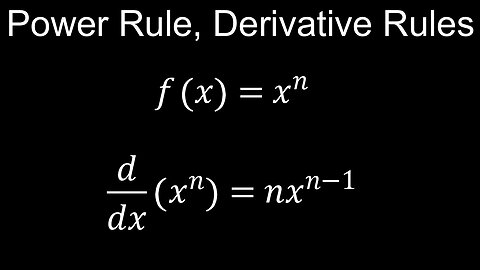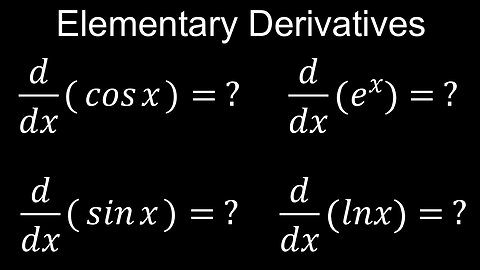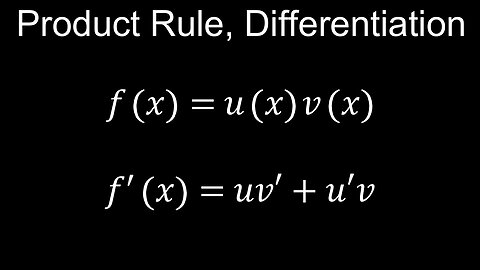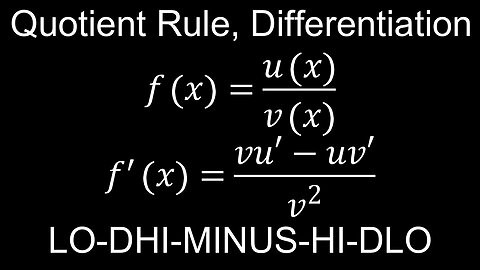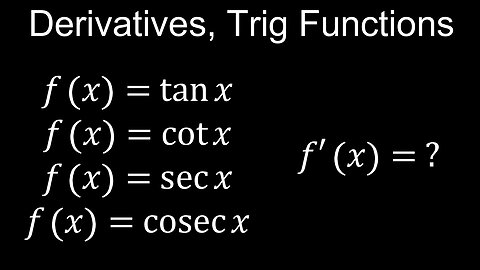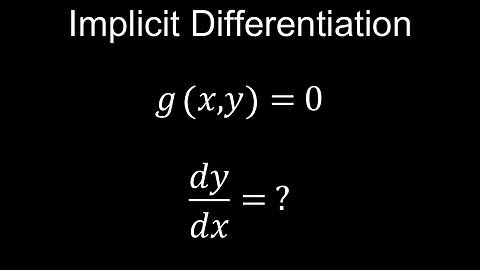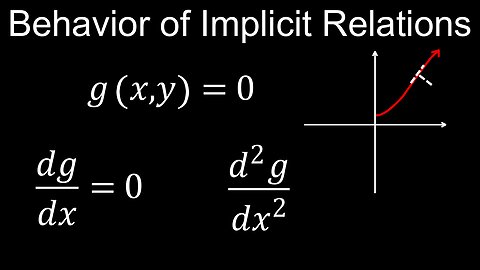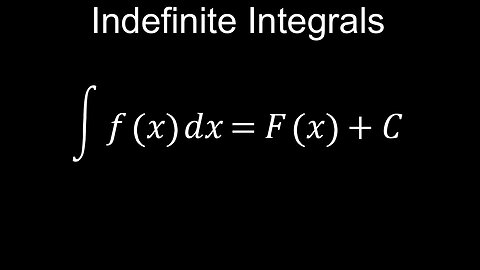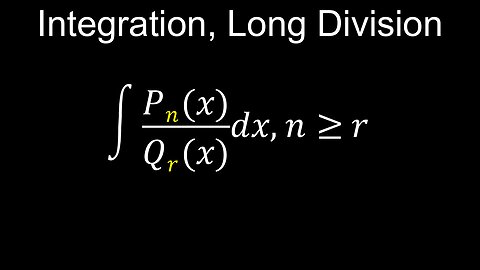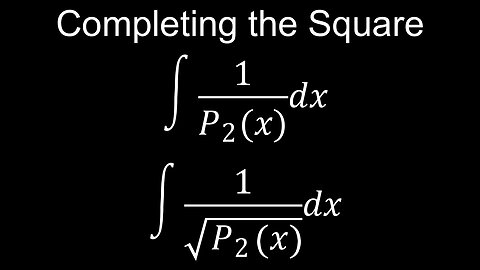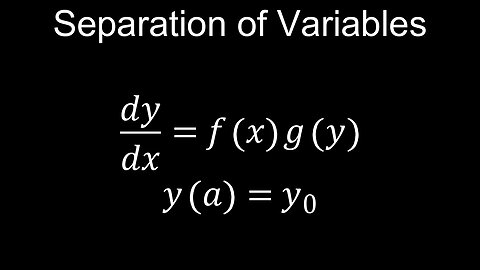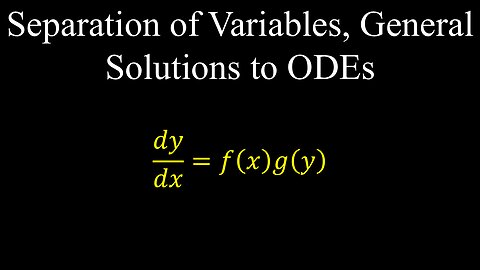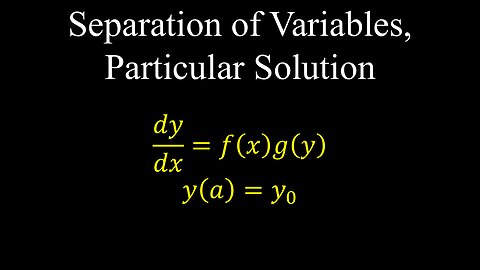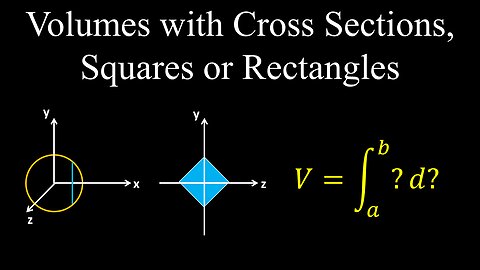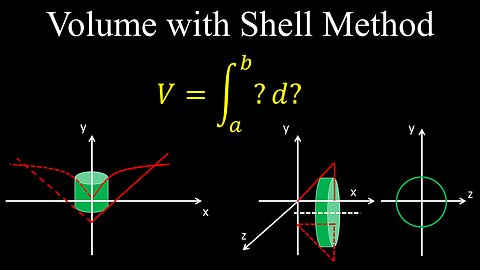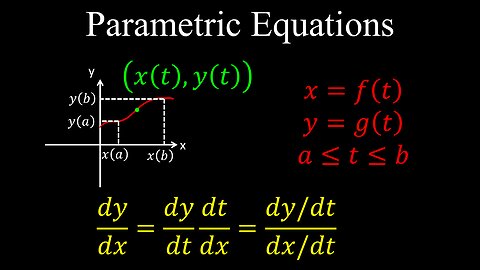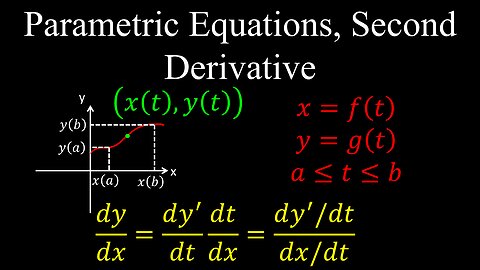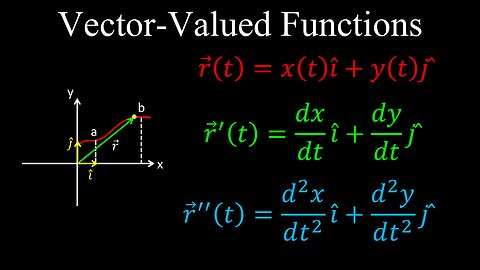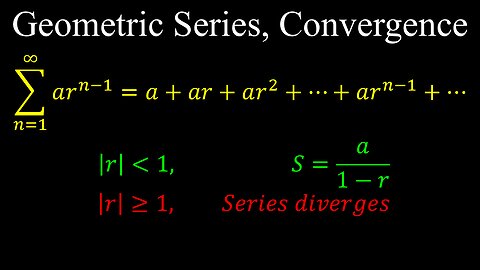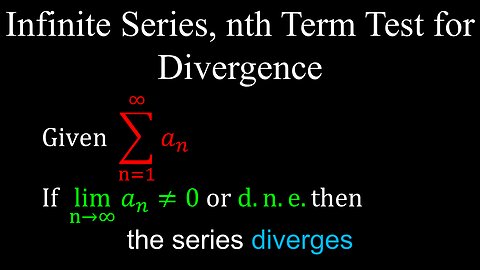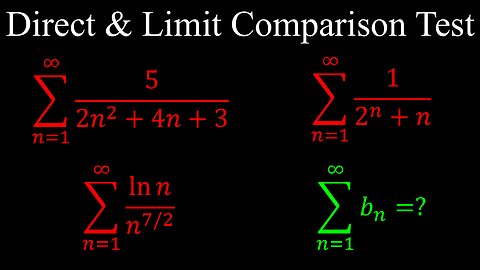Premium Only Content

Limits Explained, Definition, Examples, Worksheet, Practice Problems - Calculus
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
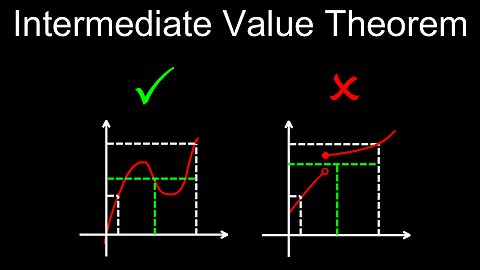
Intermediate Value Theorem, Visual Proof, Application, Exercises - Calculus
Derivative of a Function, Definition, First Principles, Geometry, Examples - Calculus
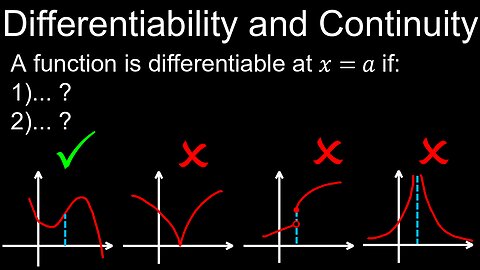
Differentiability and Continuity of Function, Rates of Change, Visual Proof, Example - Calculus
Derivative Rules, Power Rule for Differentiation - Calculus
Derivatives of Elementary Functions, sin(x), cos(x), e^x, ln(x) - Calculus
Product Rule, Differentiation, Basic Proof, Examples - Calculus
Quotient Rule for Differentiation, Mnemonic, Examples - Calculus
Derivatives of Trig Functions, Basic Proofs, tan(x), cot(x), sec(x), cosec(x), Examples - Calculus
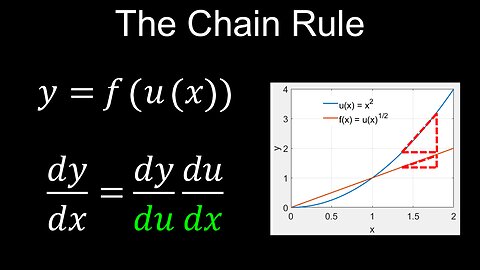
Chain Rule of Differentiation, Derivatives, Composite Functions, Examples - Calculus
Implicit Differentiation, vs Explicit, Chain Rule, Examples - Calculus
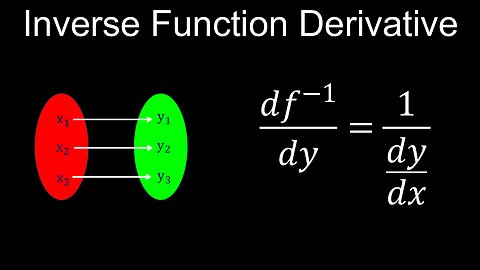
Derivatives of Inverse Functions, Basic Proof, Examples - Calculus
Derivatives of Inverse Trig Functions, Basic Proof, Examples - Calculus
Higher-Order Derivatives of Functions, Second Derivative, Examples - Calculus
Logarithmic Differentiation, Basic Proof, Exponential, Examples - Calculus
Derivatives in Context, Interpretation, Examples - Calculus
Straight Line Motion, Position, Displacement, Velocity, Acceleration, Speed, Distance - Calculus
Solving Related Rates Problems, Chain Rule, Derivatives - Calculus
Local Linearity and Error Approximation, Tangent Line, Examples - Calculus
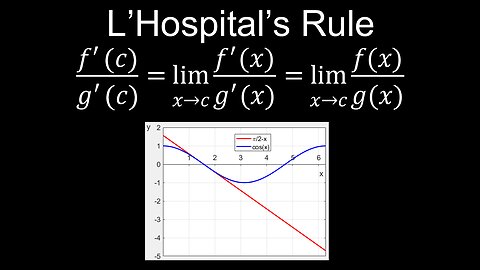
L'Hospital's Rule, Limits, Indeterminate Forms, Examples - Calculus
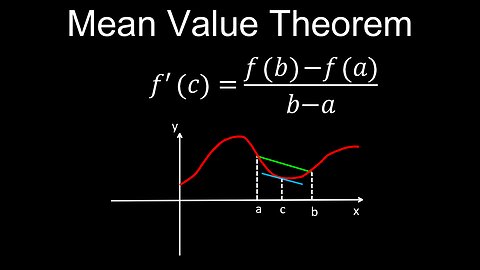
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
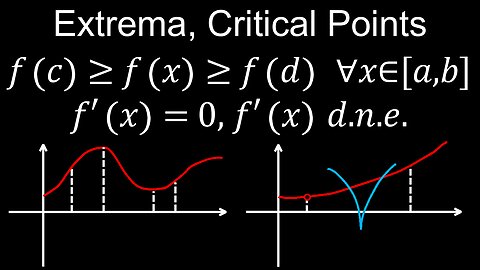
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus
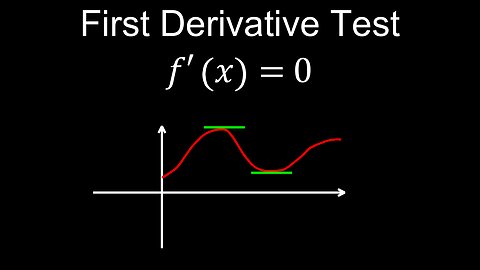
First Derivative Test, Local Extrema, Examples - Calculus
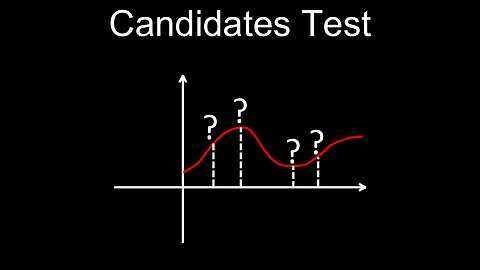
Candidates Test, Global Extrema, Example - Calculus
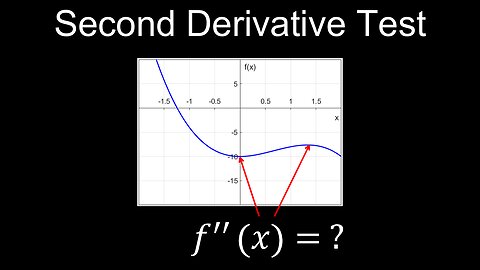
Second Derivative Test, Local Extrema, Visual Proof, Example - Calculus
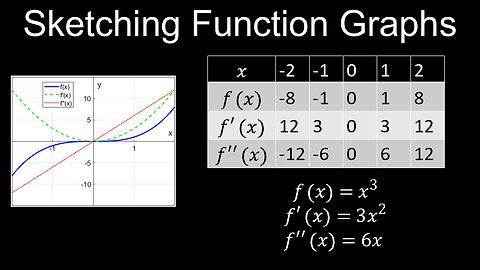
Graphs of Functions and their Derivatives, Curve Sketching, Examples - Calculus
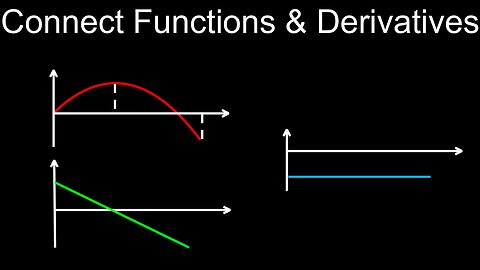
Connecting a Function and its Derivatives, Graphs, Position, Velocity, Acceleration - Calculus
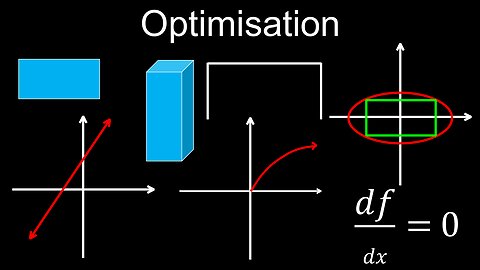
Solving Optimisation Problems, Differentiation, Examples - Calculus
Behaviour of Implicit Relations, Derivatives, Examples - Calculus
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
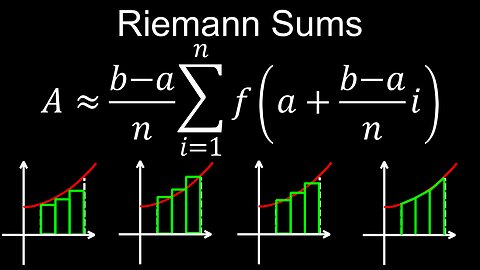
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
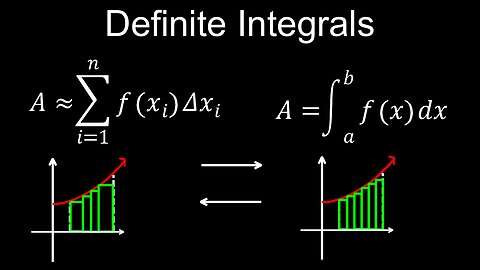
Definite Integral, Definition from Riemann sum, Formula, Symbol, Example - Calculus
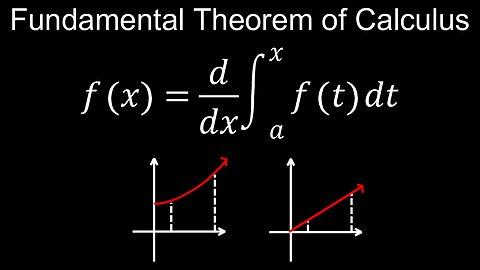
Fundamental Theorem of Calculus, Part 1, Visual Proof, Definite Integral - Calculus
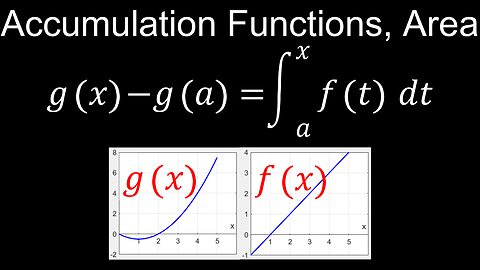
Behaviour of Accumulation Functions, Area, Graphical, Numerical, Analytical - Calculus
Definite Integrals, Formula, Properties, Rules, Integration over Discontinuities - Calculus
Fundamental Theorem of Calculus, Part 2, Definite Integrals, Basic Proof - Calculus
Indefinite Integrals, Antiderivatives, Power Rule, Trig, Inverse, Log, Exp, Examples - Calculus
Integration by Substitution Method Explained, Definite integrals, Examples - Calculus
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by Parts, Formula, Rule, Example, Order - Calculus
Integration, Partial Fractions, Formula, Irreducible Quadratic Factors, Worksheet - Calculus
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus
Selecting Integration Techniques Explained, List of Methods - Calculus
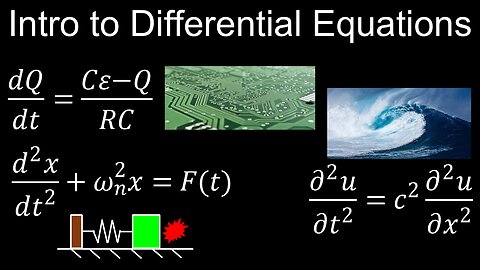
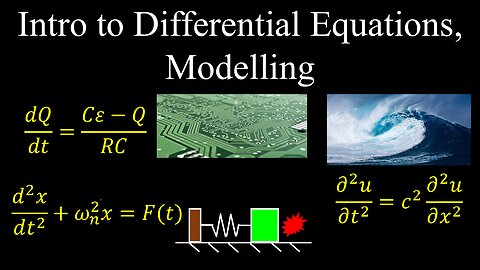
Intro to Differential Equations, Modelling, Worksheet, Example - Calculus
Verifying Solutions to Differential Equations, Examples - Calculus
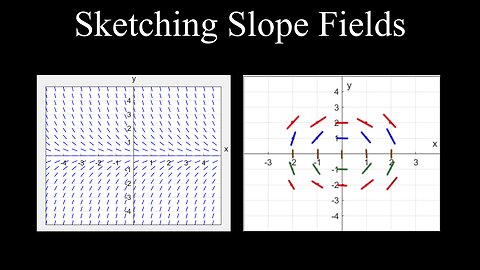
Sketching Slope Fields and Solution Curves Explained, Differential Equations, Example - Calculus
Euler's Method for Solving Differential Equations Explained, Example - Calculus
Separation of Variables Method, Differential Equations, Integration, Examples - Calculus
Exponential Models with Differential Equations, Population Growth, Examples - Calculus
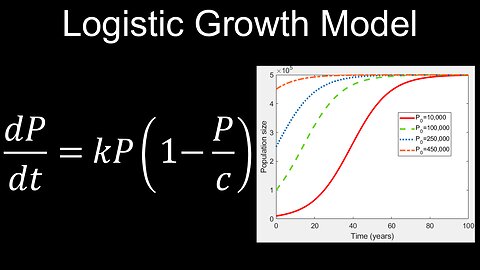
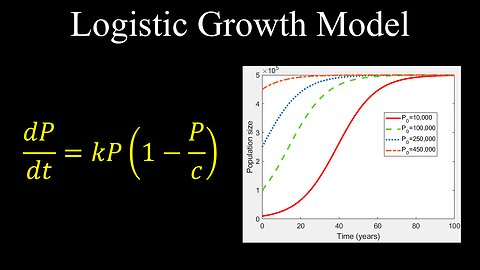
Logistic Growth Differential Equation, Model, Example - Calculus
Mean Value Theorem for Integrals, Visual Proof, Examples, Practice Problems - Calculus
Connecting Position, Velocity, Acceleration of Functions, Integrals, Straight Line Motion - Calculus
Intro to Differential Equations, Modelling - Calculus
Verifying Solutions to Differential Equations - Calculus
Sketching Slope Fields, Differential Equations - Calculus
Sketching Solution Curves, Slope Fields - Calculus
Euler's Method, Approximating Solutions to ODEs, Example - Calculus
Separation of Variables, General Solution, ODEs - Calculus
Separation of Variables, Particular Solution, Differential Equations, Examples - Calculus
Exponential Models, Growth, Decay, Differential Equations - Calculus
Logistic Growth Model, Differential Equations - Calculus
Mean Value Theorem, Integration, Average Value, Continuous Function - Calculus
Displacement Vs Distance, Speed Vs Velocity, Acceleration, Integration - Calculus
Definite Integrals, Applied Contexts, Accumulation Functions - Calculus
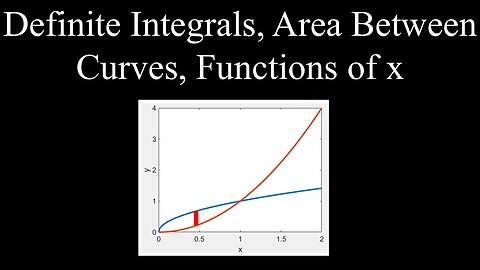
Definite Integrals, Area Between Curves, Functions of x - Calculus
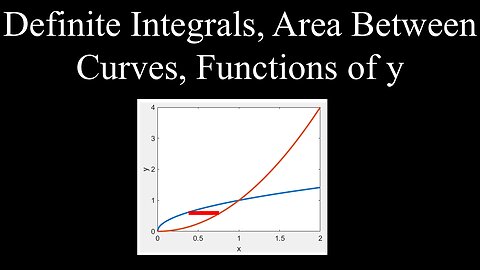
Definite Integrals, Area Between Curves, Functions of y - Calculus
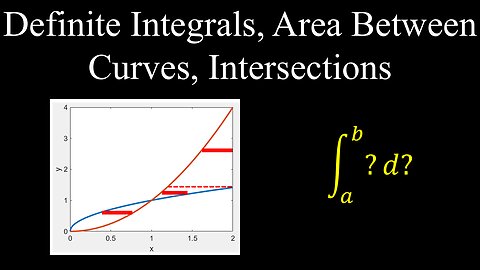
Definite Integrals, Area Between Two Curves, Intersection Points - Calculus
Volumes with Cross Sections, Squares and Rectangles, Examples - Calculus
Volumes with Cross Sections, Triangles and Semicircles, Examples - Calculus
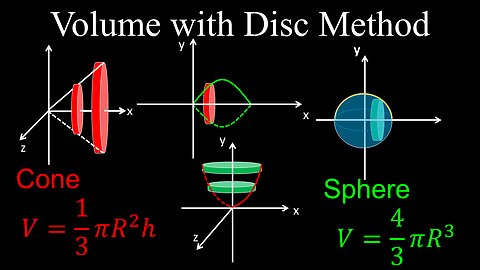
Volume with the Disk Method, Revolved Solid Around x or y axis, Cone, Sphere - Calculus
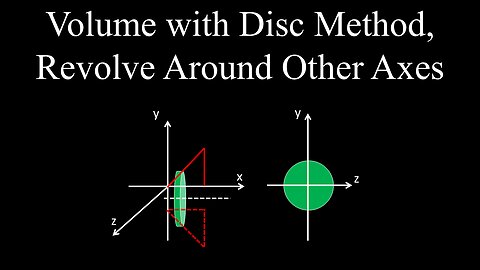
Volume with the Disk Method, Revolving Around other Axes - Calculus
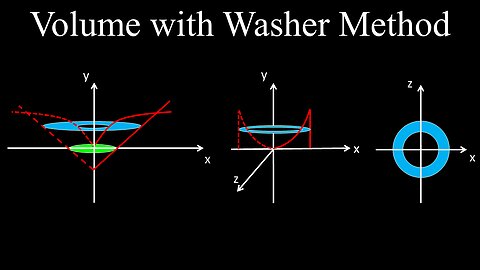
Washer Method to Find the Volume of a Revolved Solid - Calculus
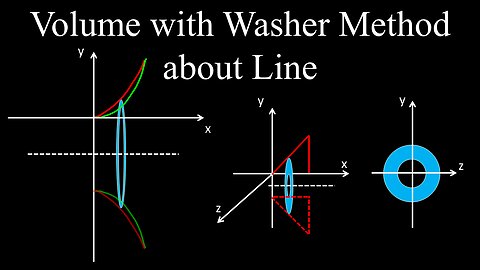
Volume with the Washer Method, Revolved Solid Around Line - Calculus
Arc Length, Planar Curve, Distance, Definite Integral - Calculus
Volume of Revolved Solid, Cylindrical Shell Method, Integration - Calculus
Parametric Equations, Definition, Differentiation - Calculus
Parametric Equations, Second Derivative - Calculus
Parametric Curve, Arc Length, Distance - Calculus
Vector-Valued Functions, Differentiation, Examples - Calculus
Vector-Valued Function, Integration - Calculus
Vector-Valued Functions and Motion in 2D Space - Calculus
Polar Coordinates, Polar Curves, Differentiation - Calculus
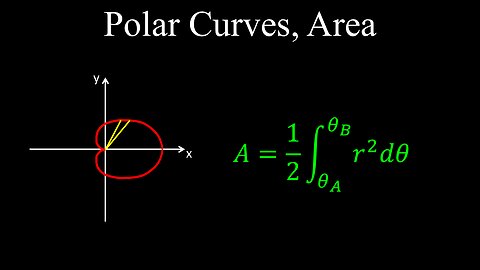
Polar Curve, Area of Region, Integration - Calculus
Polar Curve, Area of Region between Two Curves, Examples - Calculus
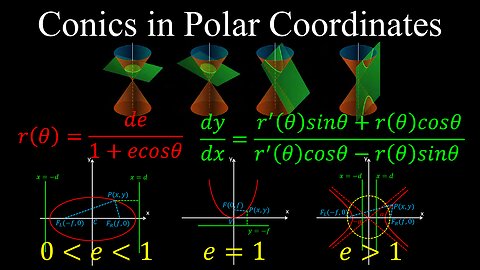
Conics in Polar Coordinates, Derivatives, Example - Calculus
Infinite Sequence, Definition, Representations, Convergence - Calculus
Infinite Series, Definition, Partial Sum, Convergence - Calculus
Geometric Series, Sum, Convergence - Calculus
nth Term Test, Divergence, Infinite Series, Examples - Calculus
Integral Test, Convergence, Infinite Series, Example - Calculus
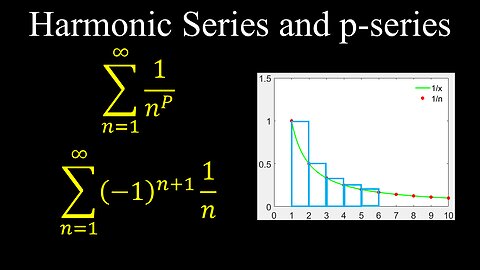
Harmonic Series, p-series, Alternating, Convergence, Examples - Calculus
Direct and Limit Comparison Tests, Infinite Series, Convergence - Calculus
Alternating Series Test, Infinite Series - AP Calculus BC
Ratio Test, Infinite Series, Convergence, Examples - Calculus
Absolute and Conditional Convergence, Infinite Series, Examples - Calculus
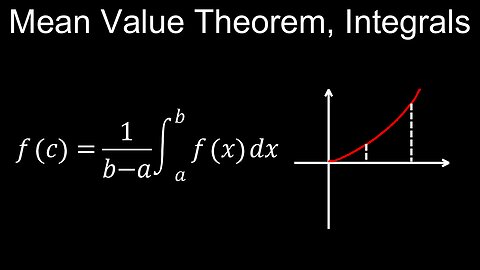
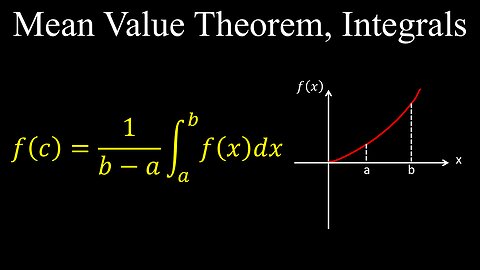
Mean Value Theorem for Integrals, Visual Proof, Examples, Practice Problems - Calculus
The Mean Value Theorem for Integrals states that for a continuous function \(f(x)\) on a closed interval \([a,b]\), there is at least one point \(c\) within the interval where the function's value \(f(c)\) equals the function's average value over the interval, given by \(\frac{1}{b-a}\int _{a}^{b}f(x)\,dx\). Mathematically, this is expressed as \(f(c)=\frac{1}{b-a}\int _{a}^{b}f(x)\,dx\), or equivalently, \(\int _{a}^{b}f(x)\,dx=f(c)(b-a)\). This means a rectangle with width \((b-a)\) and height \(f(c)\) will have the same area as the definite integral of \(f(x)\) over the interval [a, b].
💡Key Aspects of the Theorem
• Continuity is Required: The function \(f(x)\) must be continuous on the closed interval \([a,b]\).
• Existence of 'c': The theorem guarantees that at least one such point \(c\) exists within the interval, but it does not provide a method to find \(c\). • Average Value: The value \(f(c)\) represents the average height of the function over the interval.
• Geometric Interpretation: Geometrically, the theorem states that for a continuous function, there exists a rectangle with height \(f(c)\) and width \((b-a)\) that has the same area as the region under the curve of \(f(x)\) from \(a\) to \(b\).
💡Mathematical Statement
• If \(f(x)\) is continuous on the closed interval \([a,b]\), then there exists a number \(c\in [a,b]\) such that:
\(f(c)=\frac{1}{b-a}\int _{a}^{b}f(x)\,dx\)
• Or, this can be rearranged to:
\(\int _{a}^{b}f(x)\,dx=f(c)(b-a)\)
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1GQtYzPXeZpvnm7EdpOAPfEyr-VSltAse/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1urkbDfPaDPsymE8T58TZZJHgeUw-P-qx/view?usp=drive_link
💡Chapters:
00:00 Mean value theorem for integrals
01:00 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 2:47:40
2:47:40
Barry Cunningham
4 hours agoBREAKING NEWS: WATCH PARTY WITH PRESIDENT TRUMP ON THE LAURA INGRAHAM SHOW (AND MORE NEWS)
120K15 -
 2:36:50
2:36:50
Blabs Games
10 hours agoLet's Get Those 5 Stars! Jurassic World Evolution 3 Playthrough #7
8.37K1 -
 LIVE
LIVE
Flyover Conservatives
20 hours ago$117K Paywall to Protect School’s Indoctrination? The Education System’s Biggest Secret w/ Nicole Solas | FOC Show
245 watching -
 UPCOMING
UPCOMING
We Like Shooting
13 hours agoWe Like Shooting 636 (Gun Podcast)
189 -

RiftTV
3 hours agoFBI Director Kash Patel Sues Elijah Schaffer for $5 MILLION?!
21.8K6 -
 LIVE
LIVE
DannyStreams
48 minutes agoPutting this here until we get noticed
13 watching -
 LIVE
LIVE
SOLTEKGG
1 hour ago🔴LIVE - Battlefield 6 REDSEC (30+ KILL WORLD RECORD)
60 watching -
 50:26
50:26
BonginoReport
9 hours agoElections Post-Mortem with Mayor Scott Singer - Nightly Scroll w/ Hayley Caronia (Ep.174)
75.4K19 -
 LIVE
LIVE
XDDX_HiTower
1 hour agoARC RAIDERS, FIRST DROP IN
55 watching -
 LIVE
LIVE
Eternal_Spartan
11 hours ago🟢 Eternal Spartan Plays Resident Evil 8 | USMC Veteran
48 watching