Polar Coordinates, Cartesian Coordinates, Spherical Coordinates
saxi753
- 2 / 3
1
Evaluate ∭_E z dV where E lies above the paraboloid z=x^2+y^2 and below the plane z=2y
12:59

Evaluate ∭_E z dV where E lies above the paraboloid z=x^2+y^2 and below the plane z=2y

Evaluate ∭_E z dV where E lies above the paraboloid z=x^2+y^2 and below the plane z=2y #PolarCoordinates #Techniuqes #Evaluate #TripleIntegrals
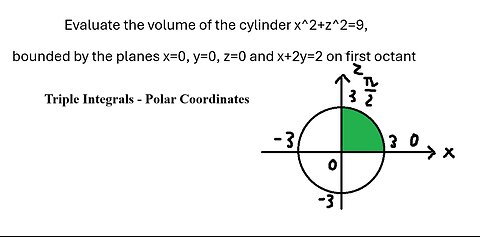
Polar Coordinates: Evaluate the volume of the cylinder x^2+z^2=9, bounded by the planes
8:36

Polar Coordinates: Evaluate the volume of the cylinder x^2+z^2=9, bounded by the planes

Evaluate the volume of the cylinder x^2+z^2=9, bounded by the planes x=0, y=0, z=0 and x+2y=2 on first octant Here is the technique to solve the question related to polar coordinates and how to find them in step-by-step #Calculus #Techniques #PolarCoordinates #TripleIntegrals
3
Transform the polar equation:r=4cosθ/(cos^2⁡θ+1) into its Cartesian form and identify the curve
3:30

Transform the polar equation:r=4cosθ/(cos^2⁡θ+1) into its Cartesian form and identify the curve

Here is the technique to solve the question related to polar coordinates and how to find them in step-by-step #PolarCoordinates #Calculus #CartesianForm #Solutions

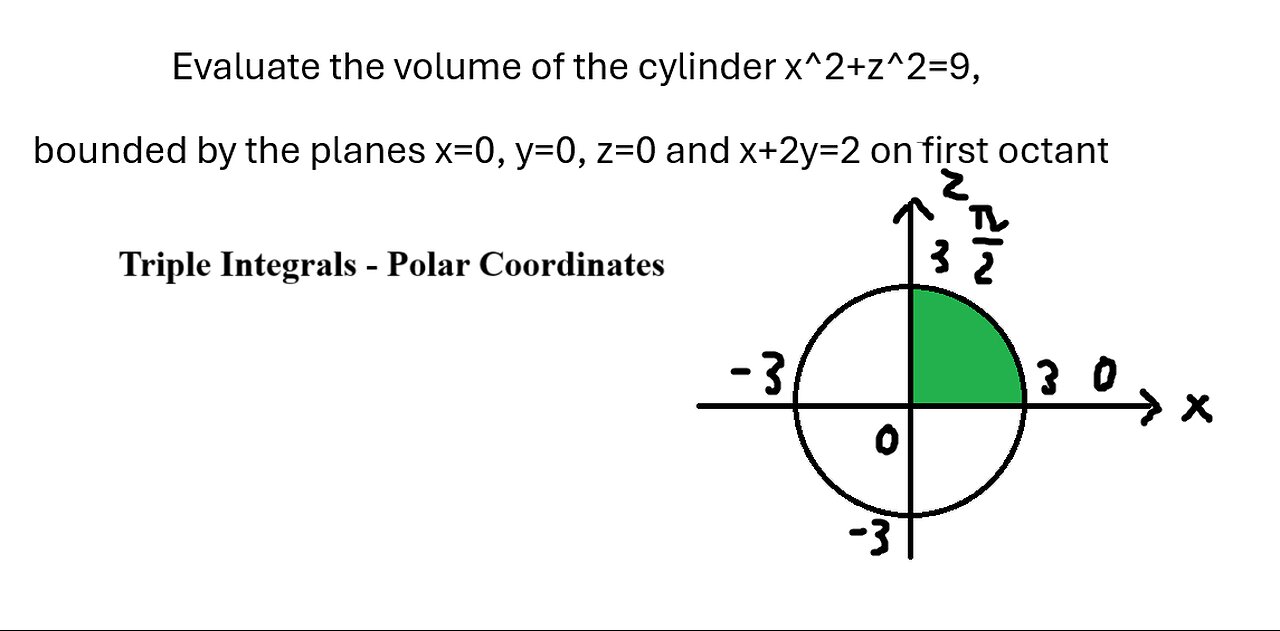
Polar Coordinates: Evaluate the volume of the cylinder x^2+z^2=9, bounded by the planes

Save
10 months ago
21
Health & Science Calculus Techniques PolarCoordinates TripleIntegrals

Evaluate the volume of the cylinder x^2+z^2=9,
bounded by the planes x=0, y=0, z=0 and x+2y=2 on first octant

Here is the technique to solve the question related to polar coordinates and how to find them in step-by-step

#Calculus
#Techniques
#PolarCoordinates
#TripleIntegrals

Loading comments...