Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.

Toán Cao Cấp - Toán Giải Tích Đại Học
saxi753
- 65 / 67
1
Toán Cao Cấp: Tìm giới hạn: Lim {x→1} (x^10 + 2x^5 - 3) / (x^10 + x^5 - 2) - L'Hospital
saxi753
Toán Cao Cấp: Tìm giới hạn: Lim {x→1} (x^10 + 2x^5 - 3) / (x^10 + x^5 - 2) - L'Hospital
#ToanCaoCap
#LHospital
#GioiHan
#CachGiai
2
Toán Cao Cấp: lim(x→0^+ ) x^(cosx-1) - Sử dụng L'Hospital - Cách Giải
saxi753
Toán Cao Cấp: lim(x→0^+ ) x^(cosx-1) - Sử dụng L'Hospital - Cách Giải
#ToanCaoCap
#CachGiai
#Limit
#LHospital
3
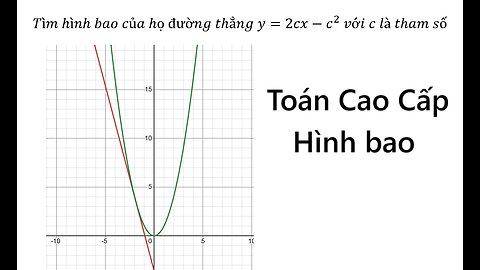
Toán Cao Cấp: Tìm hình bao của họ đường thẳng y=2cx-c^2 với c là tham số
saxi753
Tìm hình bao của họ đường thẳng y=2cx-c^2 với c là tham số
#ToanCaoCap
#TimHinhBao
#CachGiai
#ToanDaiHoc
4
Toán Cao Cấp: Toán Giới hạn - lim(x→1) (3^(x-1)-1)/(x-1) - Cách giải
saxi753
Toán Cao Cấp: Toán Giới hạn - lim(x→1) (3^(x-1)-1)/(x-1) - Cách giải
5
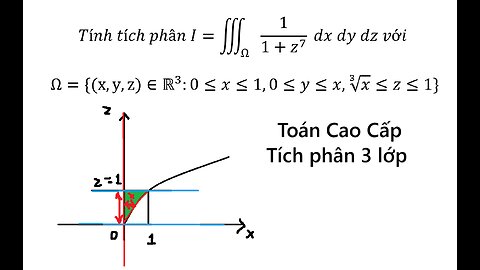
Tính tích phân I=∭_Ω▒1/(1+z^7 ) dx dy dz với Ω={(x,y,z)∈R^3:0≤x≤1,0≤y≤x,∛x≤z≤1}
saxi753
Tính tích phân I=∭_Ω▒1/(1+z^7 ) dx dy dz với
Ω={(x,y,z)∈R^3:0≤x≤1,0≤y≤x,∛x≤z≤1}
#ToanCaoCap
#TichPhan3Lop
#CachGiai
#Integral
#TripleIntegrals
#Integrations
6
Toán Cao Cấp: Cho trường lực F=(6xyz-2y^4+z^3,3x^2 z-8y^3 x,3x^2 y+3xz^2 )
saxi753
Cho trường lực F ⃗=(6xyz-2y^4+z^3,3x^2 z-8y^3 x,3x^2 y+3xz^2 )
a) Chứng minh rằng F ⃗ là một trường thế
b) Tính công của trường lực F ⃗ khi di chuyển một vật từ A(2,1,-1) đến B(1,-2,2)
7
Toán Cao Cấp: Định lý Gauss: Tính ∬_S▒(x dydz+y dzdx+z dxdy)/(x^2+y^2+z^2 ) với S là mặt biên
saxi753
Tính ∬_S▒(x dydz+y dzdx+z dxdy)/(x^2+y^2+z^2 ) với S là mặt biên xác định theo hướng pháp tuyến
ngoài của miền {(x,y,z)|1≤x^2+y^2+z^2≤4}
#ĐịnhLýGauss
#ToanCaoCap
#CachGiai
#ToanDaiHoc
#GiaiTich
8
Toán Cao Cấp: Định lý Green: Cho C là đường elip 9x^2+4y^2=36 Tính ∮_C (x+2y)dx+(3x^2-4y)dy
saxi753
Cho C là đường elip 9x^2+4y^2=36
Tính ∮_C (x+2y)dx+(3x^2-4y)dy lấy theo hướng ngược chiều kim đồng hồ
#DinhLyGreen
#ContourIntegral
#Integration
#TichPhanDoiBien
9
Toán Cao Cấp: Hàm Gamma - Bách Khoa: ∫_0^1 x^7 ∛(1-x^3 ) dx - Tích phân đổi biến
saxi753
Toán Cao Cấp: Hàm Gamma - Bách Khoa: ∫_0^1 x^7 ∛(1-x^3 ) dx - Tích phân đổi biến
#ToanCaoCap
#GiaiTich
#HamGamma
#BachKhoa
#Integral
#Integration
#TichPhanDoiBien
10
Toán Cao Cấp: Tính độ cong của đường cong y=3x^2+5x+3 tại điểm (0;3)
saxi753
Toán Cao Cấp: Tính độ cong của đường cong y=3x^2+5x+3 tại điểm (0;3)
11
Toán Cao Cấp: Khai triển Maclaurin: lim (x→0) (tanx-x-1/3 x^3)/x^5
saxi753
Toán Cao Cấp: Khai triển Maclaurin: lim (x→0) (tanx-x-1/3 x^3)/x^5
#ToanCaoCap
#ChuongTrinhMoi
#KhaiTrienMaclaurin
12
Toán Cao Cấp: Phương trình vi phân Cauchy-Euler - x^2 y''+xy'-y=0
saxi753
Giải phương phương trình vi phân tuyến tính cấp hai có hệ số biến thiên
(Phương trình vi phân Cauchy-Euler)
x^2 y''+xy'-y=0
#ToanCaoCap #PhuongTrinhViPhanCapHai #CauchyEuler #CachGiai
13
Toán Cao Cấp - Bách Khoa: Hàm Gamma - Tích phân đổi biến: ∫_0^(π/4) ∛(sin^11 (2x) cos^7(2x) ) dx
saxi753
Toán Cao Cấp - Bách Khoa: Hàm Gamma - Tích phân đổi biến: ∫_0^(π/4) ∛(sin^11 (2x) cos^7(2x) ) dx
#ToanCaoCap
#HamGamma
#ToanGiaiTich
#ToanDaiHoc
14
Toán Cao Cấp: Cho hàm số z=y arctan(3x^2+2y).Tính dz(1;-1) Vi phân toàn phần
saxi753
Cho hàm số z=y arctan(3x^2+2y).Tính dz(1;-1)
Vi phân toàn phần
15
Toán Cao Cấp: Tích phân: ∫_0^1 arccot(√x) dx - Tích phân đổi biến - Tích phân từng phần
saxi753
∫_0^1▒〖arccot(√x) dx〗
Tích phân đổi biến
#ToanCaoCap
#ToanDaiHoc
#TichPhanTungPhan
#TichPhanDoiBien
#CachGiai
16
Toán Cao Cấp: Tích phân đường loại 1: Cho C là đường elip 9x^2+4y^2=36. Tính ∫_(C_1) xy ds
saxi753
Cho C là đường elip 9x^2+4y^2=36
Tính ∫_(C_1) xy ds ,trong đó C_1 là phần C trong góc phần tư nhứ nhất
17
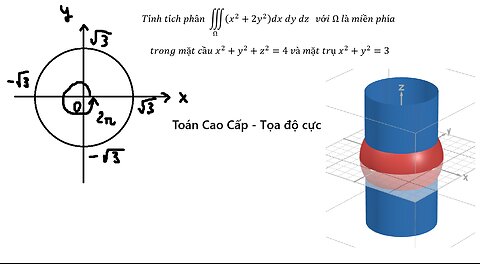
Toán Cao Cấp: Tính tích phân ∭ Ω (x^2+2y^2 )dx dy dz với Ω là miền phía trong mặt cầu x^2+y^2+z^2=4
saxi753
Tính tích phân ∭ Ω (x^2+2y^2 )dx dy dz với Ω là miền phía
trong mặt cầu x^2+y^2+z^2=4 và mặt trụ x^2+y^2=3
18
Toán Cao Cấp: lim (x→0) (∫_0^(x^2026) (5t^3+sint)dt+xe^x)/(ln(x+1)+arctanx+sinx)
saxi753
Toán Cao Cấp: lim (x→0) (∫_0^(x^2026) (5t^3+sint)dt+xe^x)/(ln(x+1)+arctanx+sinx)
19
Toán Cao Cấp: Cho biết hàm doanh thu cận biên của doanh nghiệp sản xuất độc quyền 1 loại hàng
saxi753
Cho biết hàm doanh thu cận biên của doanh nghiệp sản xuất độc quyền 1 loại hàng hoá là MR(Q)=40-0,45Q^2. Xác định hàm tổng doanh thu và hàm cầu hàng hoá của doanh nghiệp. Tính hệ số co giãn của cầu theo giá tại mức giá p=30 và nêu ý nghĩa của kết quả tính được.
20
Toán Cao Cấp: Làm cách nào nhớ công thức Vô cùng bé tương đương hay bị quên trong giải tích 1 và 2 ?
saxi753
Toán Cao Cấp: Làm cách nào nhớ công thức Vô cùng bé tương đương hay bị quên trong giải tích 1 và 2 ?
21
Toán Giải tích 1: L'Hospital (Giả sử đề THPT khó): Cho lim (x→2/3) (√(mx+2)-√n)/(3x-2) = 1/4
saxi753
Toán Giải tích 1: L'Hospital (Giả sử đề THPT khó): Cho giới hạn của hàm số lim┬(x→2/3)〖(√(mx+2)-√n)/(3x-2)〗=1/4 .
Tính giá trị của biểu thức m+n
22
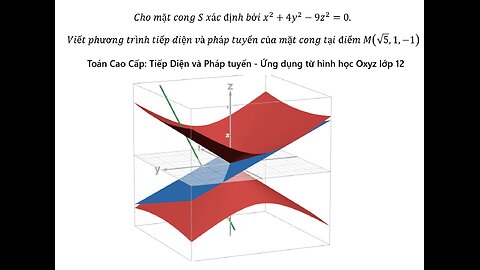
Toán Cao Cấp: tiếp diện và pháp tuyến: Cho mặt cong S xác định bởi x^2+4y^2-9z^2=0.
saxi753
Cho mặt cong S xác định bởi x^2+4y^2-9z^2=0.
Viết phương trình tiếp diện và pháp tuyến của mặt cong tại điểm M(√5,1,-1)
23
Toán Cao Cấp: Khai triển Mac-laurin: Cho hàm số y=(2x+1) sin(4x^2 ).Tính đạo hàm
saxi753
Toán Cao Cấp: Khai triển Mac-laurin: Cho hàm số y=(2x+1) sin(4x^2 ).Tính đạo hàm y^((11)) (0)
24
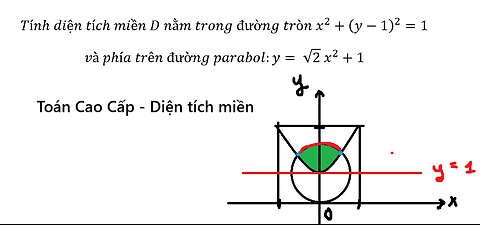
Toán Cao Cấp: Tính diện tích miền D nằm trong đường tròn x^2+(y-1)^2=1
saxi753
Tính diện tích miền D nằm trong đường tròn x^2+(y-1)^2=1
và phía trên đường parabol:y= √2 x^2+1
25
Toán Cao Cấp: lim (x→0) (ln(1+xtanx))/(x^2+sin^3x ) - Lô-pi-tan (L'Hospital) - Cách giải
saxi753
Toán Cao Cấp: lim (x→0) (ln(1+xtanx))/(x^2+sin^3x ) - Lô-pi-tan (L'Hospital) - Cách giải
#LHospital
#Lopitan
#CachGiai
26
Toán Cao Cấp: Giới hạn: lim (x→+∞) ((x^2+2)/(x^2+5))^2x - Cách giải chi tiết
saxi753
Toán Cao Cấp: Giới hạn: lim (x→+∞) ((x^2+2)/(x^2+5))^2x - Cách giải chi tiết
#ToanCaoCap
#GiaiTich
#Limit
#GioiHan
27
Toán Cao Cấp: Giới hạn: lim (x→∞) x ln((x+e)/(x-e)) #GioiHan #LHospital #Lopitan #CachGiai
saxi753
Toán Cao Cấp: Giới hạn: lim (x→∞) x ln((x+e)/(x-e)) #GioiHan #LHospital #Lopitan #CachGiai
28
Toán Cao Cấp: Lô-pi-tan (L'Hospital): lim (x→0) (5^x-4^x)/(x^2+x) #LHospital #Limit #GioiHan
saxi753
Toán Cao Cấp: Lô-pi-tan (L'Hospital): lim (x→0) (5^x-4^x)/(x^2+x) #LHospital #Limit #GioiHan
29
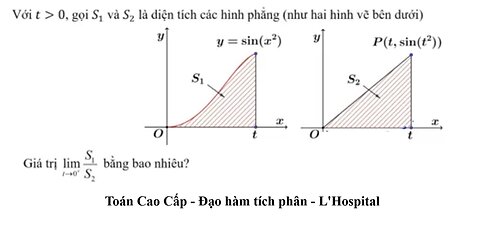
Toán Cao Cấp: Gọi S1 và S2 là diện tích các hình phẳng (như hai hình vẽ bên dưới). Lim S1/S2
saxi753
#ToanCaoCap
#DaoHamTichPhan
#LHospital
#Lopitan
30
Toán 12: Cho hàm số f(x) thỏa mãn f(1)=4 vàf(x)=xf'(x)-2x^3-3x^2 với mọi x≫0Giá trị của f(2) bằng
saxi753
Toán 12: Cho hàm số f(x) thỏa mãn f(1)=4 vàf(x)=xf'(x)-2x^3-3x^2 với mọi x≫0Giá trị của f(2) bằng
Cho hàm số f(x) thỏa mãn f(1)=4 và
f(x)=xf'(x)-2x^3-3x^2 với mọi x≫0
Giá trị của f(2) bằng
#toanlop12
#ViPhan
#differentialequation
#Calculus
31
Toán giải tích: lim(x→1) (x^n-1)/(x-1) - L'Hospital (Lô-pi-tan) #LHospital #ToanDaiHoc
saxi753
Toán giải tích: lim(x→1) (x^n-1)/(x-1) - L'Hospital (Lô-pi-tan) #LHospital #ToanDaiHoc
32
Korean CSAT: Tính giá trị của biểu thức lim (x→0) ln(1+3x)/ln(1+5x) #LHospital #Limit #GioiHan
saxi753
Korean CSAT: Tính giá trị của biểu thức lim (x→0) ln(1+3x)/ln(1+5x) #LHospital #Limit #GioiHan
33
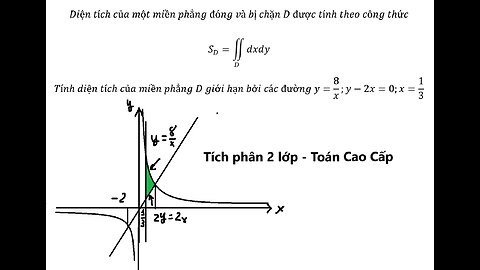
Diện tích của một miền phẳng đóng và bị chặn D được tính theo công thức S_D=∬_D dxdy
saxi753
Diện tích của một miền phẳng đóng và bị chặn D được tính theo công thức
S_D=∬_D▒dxdy
Tính diện tích của miền phẳng D giới hạn bởi các đường y=8/x;y-2x=0;x=1/3
#ToanCaoCap
#GiaiTich
#DoubleIntegrals
#Integrations
#Calculus
34
Cho hàm số y=f(x) có đạo hàm liên tục trên R và thỏa mãn f(0)=5 f^' (x)+f(x)=2x-1.Giá trị f(1)
saxi753
Cho hàm số y=f(x) có đạo hàm liên tục trên R và thỏa mãn f(0)=5
f'(x)+f(x)=2x-1.Giá trị f(1)
#ToanLop12
#ViPhan
#PhuongTrinhViPhan
#DifferentialEquations
#Calculus
35
Toán Cao Cấp: L'Hopital (Lô-pi-tan): lim (x→0) (3-2e^3x )^(4/x) - Cách giải
saxi753
Toán Cao Cấp: L'Hopital (Lô-pi-tan): lim (x→0) (3-2e^3x )^(4/x) - Cách giải
#LHospital
#Lopitan
#ToanCaoCap
36
Toán Cao Cấp Đại Học: Tìm giá trị của a để hàm số:f(x)={ ((1-e^(2x^3-16))/(x^3-8) khi x≫2 , a+x+3
saxi753
Toán Cao Cấp Đại Học: Tìm giá trị của a để hàm số:f(x)={█((1-e^(2x^3-16))/(x^3-8) khi x>2@a+x+3 khi x≤2)┤ liên tục tại x=2
#ToanCaoCap
#ToanGiaiTich
#Lopitan
#LHospital
#CachGiai
37
Toán Cao Cấp Đại Học: Tìm giới hạn dãy có số hạng tổng quát như sauu_n=(1.2+2.3+⋯+n(n+1))/n^3
saxi753
Toán Cao Cấp Đại Học: Tìm giới hạn dãy có số hạng tổng quát như sauu_n=(1.2+2.3+⋯+n(n+1))/n^3
#ToanCaoCap
#GioiHan
#Limit
38
Toán Cao Cấp: Đạo hàm riêng z=(x^3+y^3)/(x^2+y^2 ), z=y^2 sin(x/y), z=x^(y^3 )
saxi753
Đạo hàm riêng z=(x^3+y^3)/(x^2+y^2 ), z=y^2 sin(x/y), z=x^(y^3 ) , z=arctan(y/x), z=arcsin(x-2y)
#CachGiai
#DaoHamRieng
#ImplicitDifferentiation
#Differentiation
#Derivative
#ToanCaoCap
39
Toán 12: Vi phân Bernoulli và tuyến tính bậc 1: Cho hàm số y=f(x) có đạo hàm liên tục trên R
saxi753
Cho hàm số y=f(x) có đạo hàm liên tục trên R thỏa mãn
xf(x) f^' (x)=f^2 (x)-x,∀x∈R và có f(2)=1
Tích phân ∫_0^2 f^2 (x)dx
#TichPhan
#ViPhan
#DifferentialEquations
#Integrals
#ToanCaoCap
#ToanLop12
40
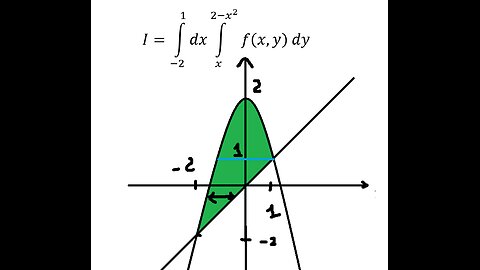
Toán Cao Cấp: Tích phân 2 lớp - Đổi cận tích phân dxdy thành dydx: I=∫(-2)^1 dx∫x^(2-x^2) f(x,y) dy
saxi753
Đổi cận tích phân dxdy thành dydx: I=∫(-2)^1 dx∫x^(2-x^2) f(x,y) dy
#ToanCaoCap
#ToanGiaiTich
#TichPhan2Lop
#DoubleIntegrals
#Integrations
41
Toán Cao Cấp: Chứng minh công thức √(x+1) ≈1+x/2 Khai triển Maclaurin
saxi753
Chứng minh công thức
√(x+1) ≈1+x/2
Khai triển Maclaurin
#MacLaurin
#KhaiTrien
#ToanCaoCap
42
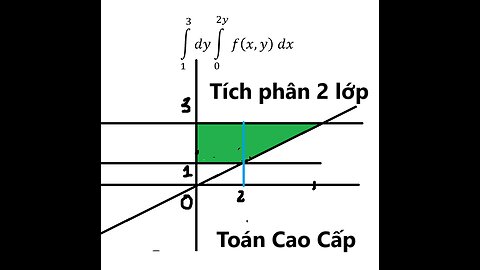
Tích phân hai lớp (Tích phân kép) - Đổi cận và đổi biến - Cơ bản: ∫_1^3 dy ∫0^2y f(x,y) dx
saxi753
Tích phân hai lớp (Tích phân kép)
∫1^3 dy ∫0^2y f(x,y) dx
#TichPhan
#DoubleIntegrals
#Integrations
#Calculus
#ToanCaoCap
43
Cho hàm số y=f(x) xác định và liên tục trên (0;+∞) thỏa mãn f(1)=1và 2xf(x)+x^2 f'(x)=3x^2+1. f(2)
saxi753
Cho hàm số y=f(x) xác định và liên tục trên (0;+∞) thỏa mãn f(1)=1và 2xf(x)+x^2 f'(x)=3x^2+1. f(2)
#ToanLop12
#ViPhanTuyenTinhBac1
#ToanCaoCap
#toan12
44
Toán Cao Cấp Đại Học: Tìm biến đổi Laplace L{(e^(-t)+1)^2 cos(2t)} - Laplace Transformation
saxi753
Toán Cao Cấp Đại Học: Tìm biến đổi Laplace L{(e^(-t)+1)^2 cos(2t)} - Laplace Transformation
#LaplaceTransformation
#ToanCaoCap
#GiaiTich
45
Cho hàm số f(x) thỏa mãn (f'(x))^2+f(x).f''(x)=x^3-2x,∀x∈Rvà f(0)=f' (0)=1.Tính T=f^2 (2) Vi phân
saxi753
Cho hàm số f(x) thỏa mãn (f'(x))^2+f(x).f''(x)=x^3-2x,∀x∈Rvà f(0)=f' (0)=1.Tính T=f^2 (2) Vi phân
#Viphan
#DifferentialEquations
#Calculus
#ToanLop12
#ToanCaoCap
46
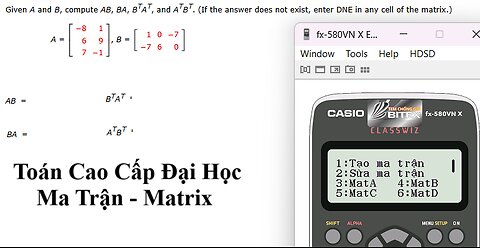
Thủ thuật CASIO: Ma Trận - Tích Ma Trận 3x2 và 2x3 - Transpose (Ma trận chuyển vị)
saxi753
Thủ thuật CASIO: Ma Trận - Tích Ma Trận 3x2 và 2x3 - Transpose (Ma trận chuyển vị)
Đây là video cách giải CASIO về Ma trận, Tích Ma Trận và Ma trận chuyển vị (Transpose)
#maths
#Matrixx
#MaTran
#Calculus
47
Toán Đại Học: Giải phương trình y^'+3/x y=2/x^3 ,y(1)=0 - Vi phân tuyến tính bậc 1
saxi753
Toán Đại Học: Giải phương trình y^'+3/x y=2/x^3 ,y(1)=0 - Vi phân tuyến tính bậc 1
#DifferentialEquations
#Calculus
#ViPhanTuyenTinhBac1
48
Toán Cao Cấp Đại Học - Lô-pi-tan và hàm Log Mũ nâng cao: lim(x→0) a (sinax/ax)^(3sinax/(ax-sinax))
saxi753
Đây là video cách giải về lim và cách dùng log, mũ, lô-pi-tan (L'Hospital) cho toán Đại Học Bách Khoa
#ToanCaoCap
#ToanCaoCapDaiHoc
#Lopitan
#LHospital
49
Toán Cao Cấp Đại Học: Tích phân suy rộng - ∫ From 0 to (+∞) e^(-x) sinx dx - Calculus
saxi753
Đây là video cách giải về tích phân suy rộng và chi tiết từng bước ∫ From 0 to (+∞) e^(-x) sinx dx
#TichPhanSuyRong
#ImproperIntegrals
#Integrations
#Calculus
50
Toán Cao Cấp Đại Học - Tìm giới hạn: Lô-pi-tan (L'Hospital): lim (x→0) (^7√( 7+2x)-^7√( 7-2x))/x
saxi753
Toán Cao Cấp Đại Học - Tìm giới hạn: Lô-pi-tan (L'Hospital): lim (x→0) (^7√( 7+2x)-^7√( 7-2x))/x
#Lopitan
#LHospital
#Limits
#Calculus
#ToanCaoCapDaiHoc
51
Toán Cao Cấp Đại Học: Tìm điểm cực trị địa phương và yên ngựa của f(x,y)=x^3+ 3xy^2- 15x - 12y
saxi753
Toán Cao Cấp Đại Học: Tìm điểm cực trị địa phương và yên ngựa của f(x,y)=x^3+ 3xy^2- 15x - 12y
#ToanCaoCap
#Calculus
#Derivative
#SaddlePoint
#DiemYenNgua
52
Vi phân tuyến tính bậc 1: Cho hàm số có đạo hàm trên R thỏa mãn (x+2)f(x)+(x+1) f'(x)=e^x
saxi753
Cho hàm số có đạo hàm trên R thỏa mãn
(x+2)f(x)+(x+1) f^' (x)=e^x và f(0)=1/2
Tính I=∫_1^2 (2x+2)f(x) dx
#ViPhanTuyenTinhBac1
#PhuongTrinhViPhan
#DifferentialEquations
#ToanCaoCap
53
Toán Cao Cấp: Tìm Lim dùng L'Hospital (Lô-pi-tan) và Log lim (x→0) (e^(4x^2 ) )^(1/ln(1+2x^2 ) )
saxi753
Đây là video về cách giải toán Cao Cấp và chi tiết từng bước
#ToanCaoCap
#Limit
#LHospital
#Calculus
#Lopitan
54
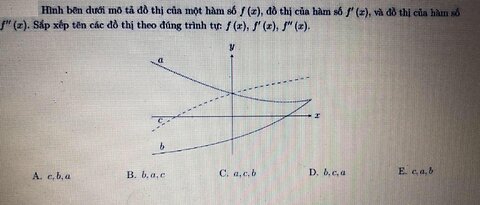
Toán 12 và Cao Cấp: Hình bên dưới mô tả f(x), f'(x), f''(x) - Chọn hình phù hợp - Derivative
saxi753
Đây là video hướng dẫn tìm f(x), f'(x), f''(x)
#KhaoSatHamSo
#DoThiHamSo
55
Phương pháp Cramer: Cho hệ phương trình tuyến tính { (x+20y=a, 3x+40y=b) trong đó tham số a,b ∈R
saxi753
Phương pháp Cramer: Cho hệ phương trình tuyến tính { (x+20y=a, 3x+40y=b) trong đó tham số a,b ∈R
#Cramer
#ToanCaoCap
#ToanGiaiTich
#Matran
#Matrix
56
Toán Cao Cấp Đại Học - L'Hospital (Lô-pi-tan) - lim (x→∞) a^x/x
saxi753
Đây là video về cách giải toán giới hạn bằng L'Hospital (Lô-pi-tan)
#CachGiai
#LHospital
#Limits
#Calculus
57
Toán Cao Cấp Đại Học: Tìm giới hạn (L'Hospital) - Lô-pi-tan lim (x→0^+ ) x lnx
saxi753
Đây là video về cách giải toán cao cấp về Lô-pi-tan (L'Hospital)
#LHospital
#Lopitan
#ToanCaoCap
#GiaiTich
#Limits
#Calculus
58
Toán Cao Cấp Đại Học - MT1003 Giải tích 1 - Đại học Bách Khoa TPHCM- Cho hàm số f khả vi trên [8,21]
saxi753
Đây là video cách giải chi tiết cho câu giải tích toán Cao Cấp Đại Học
#GiaiTich
#CaoCap
#BachKhoaTPHCM
#HamSo
#Calculus
59
Toán Cao Cấp: Giới hạn hàm số L'Hospital (Lô-pi-tan): lim (x→0) (e^2x-1)/ln(1-4x)
saxi753
Đây là cách giải chi tiết cho câu giới hạn của hàm số bằng Lô-pi-tan (L'Hospital)
#GioiHanHamSo
#ToanCaoCap
#LHospital
#Limits
60
Giải tích: Không dùng L'Hospital hay ∞/∞ : lim(x→0) (cot^2x-1/x^2 ) (Bí mật sau tấm màn)
saxi753
Đây là video về cách giải câu giải tích trên và chi tiết từng bước một
#GiaiTich
#ToanCaoCap
#Limits
#Calculus
61
Toán Cao Cấp Đại Học: L'Hospital (Lô-pi-tan) Giới hạn: lim (x→0) sin^2(x/3)/(3x^2 )
saxi753
Đây là video về cách tìm giới hạn và sử dụng L'Hospital trong bài tính giới hạn
#LHospital
#GioiHan
#CaoCapDaiHoc
62
Toán Cao Cấp Đại Học: Lô-pi-tan (L'Hospital): Giới hạn: lim (x→0) (e^ax-e^bx)/(sin(ax)-sin(bx) )
saxi753
Đây là video giải chi tiết cho cách giải về L'Hospital and Lô-pi-tan
#LHospital
#Calculus
#Derivative
63
Toán Đại Học: Định lý kẹp (Squeeze's Theorem): Tìm giới hạn Lim{x->0} x sin(1/x)
saxi753
Đây là video hướng dẫn cách giải tìm giới hạn thông qua định lý kẹp
#Squeeze'sTheorem
#DinhLyKep
#ToanCaoCap
64
Toán Đại Học: Chứng minh rằng ma trận [a b, c d] thỏa X^2 -(a+d)X + (ad-bc)I2=0
saxi753
Đây là cách giải chi tiết từng bước một cho ma trận và giải chi tiết từng bước
#MaTran
#Matrix
#Calculus
#ToanDaiHoc
Toán Đại Học: Phân tích chi tiết các mối quan hệ
saxi753
Đây là video phân tích các mối quan hệ và cách giải chi tiết
#ĐạiHọc
#QuanHệ
#Subset
#Set
66
Toán Cao Cấp: Lô-pi-tan (L'Hospital): lim(x→π/4) (( √2 sinx)^(a√2sinx)-(√2 cosx)^(a√2cosx))/(x-π/4)
saxi753
Đây là video chi tiết hướng dẫn cách giải về Lô-pi-tan (L'Hospital) và chi tiết từng bước
#LHospital
#Lopitan
#Calculus
#ToanCaoCap
67
Toán Cao Cấp Đại Học: ĐH Bách Khoa TPHCM: MT1003 - Giải tích 1: Thủ thuật CASIO: Dùng tổng Riemann
saxi753
Đây là cách giải cho cách bấm CASIO và chi tiết từng bước 1: Toán Cao Cấp Đại Học: ĐH Bách Khoa TPHCM: MT1003 - Giải tích 1: Thủ thuật CASIO: Dùng tổng Riemann
Toán Đại Học: Phân tích chi tiết các mối quan hệ
9 months ago
22
Đây là video phân tích các mối quan hệ và cách giải chi tiết
#ĐạiHọc
#QuanHệ
#Subset
#Set
Loading comments...
-
 LIVE
LIVE
Donut Operator
3 hours agoLIVE POLICE CHASE/ CRIME/ CYCLISTS ARE SCUM/ GAMEBOY CAMERA CHAD
1,564 watching -
 LIVE
LIVE
Winston Marshall
51 minutes ago"This is SHAMEFUL!” Ireland’s New Religion and It's Darkest Secret | Brendan O'Neill
587 watching -
 LIVE
LIVE
Barry Cunningham
2 hours agoPRESIDENT TRUMP IS TAKING AMERICA INTO THE GOLDEN AGE OF PROSPERITY!
1,769 watching -
 LIVE
LIVE
Sean Unpaved
2 hours agoNFL 2025: Teddy's Trouble, Dak's Narrative Shift, Purdy's Prove-It Year, & Raiders' Rebuild
153 watching -
 LIVE
LIVE
Side Scrollers Podcast
3 hours agoElon Musk Creates GOONING AI, DSP Lawsuit?, Disney Adults Hit NEW LOW | Side Scrollers Live
269 watching -
 LIVE
LIVE
Viss
2 hours ago🔴LIVE - Learn How to Dominate The Duo Battleground! - PUBG
165 watching -
 1:09:40
1:09:40
Coin Stories with Natalie Brunell
4 hours agoEpstein Files EXPOSED: CIA Black Ops, Money Crimes & Bitcoin's Rise
5.12K -
 LIVE
LIVE
GloryJean
4 hours agoTR2ing til it's nerfed 🖱️ 6.7 K/D
74 watching -
 1:07:30
1:07:30
Timcast
2 hours agoDemocrat Impeachment Leader Schiff ACCUSED OF FRAUD, Trump DOJ Targets Anti-Trump CONSPIRACY
145K74 -
 2:09:35
2:09:35
Nikko Ortiz
3 hours agoLive - AI Has Gone Too Far
83.2K4
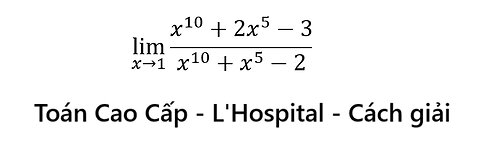
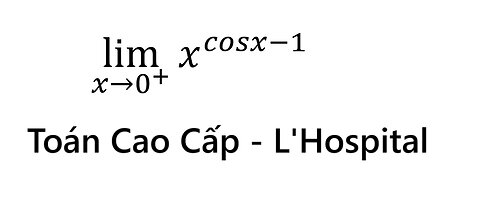
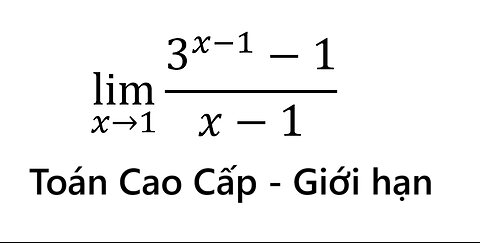



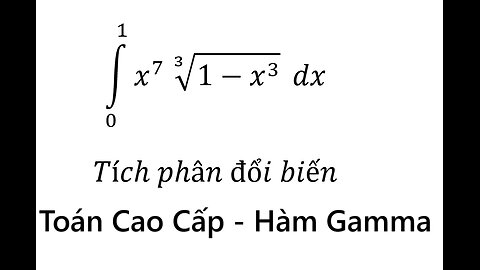

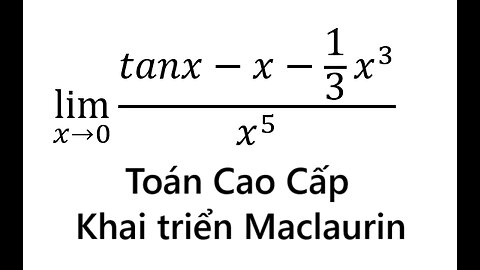










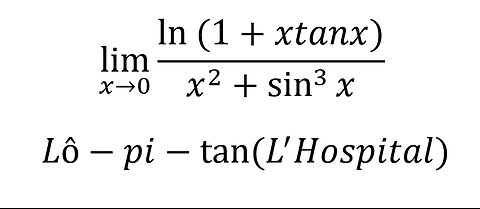

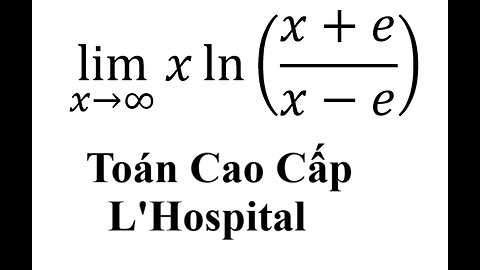
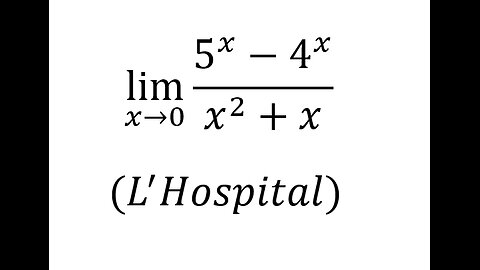

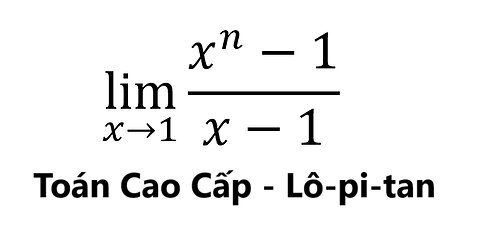


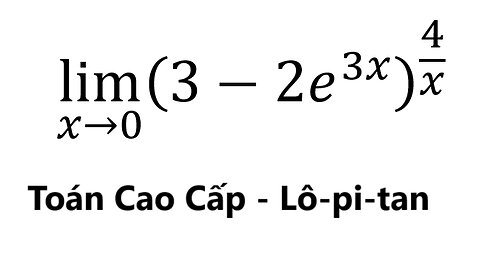








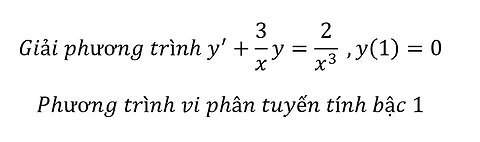

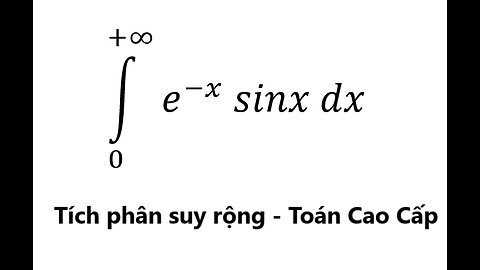

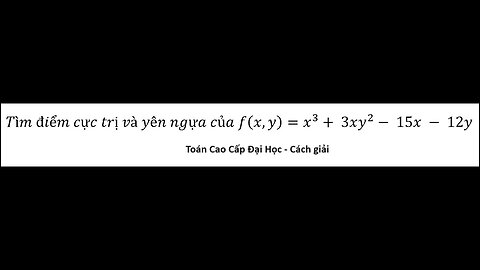
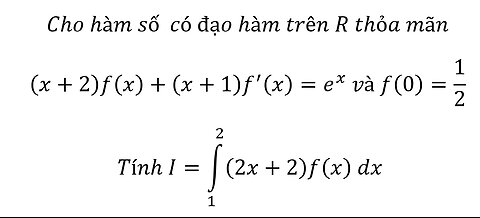


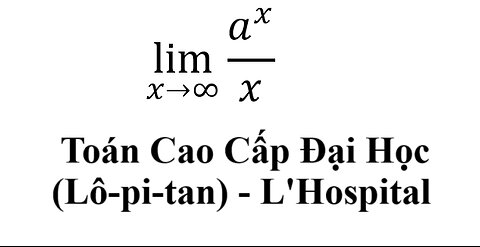
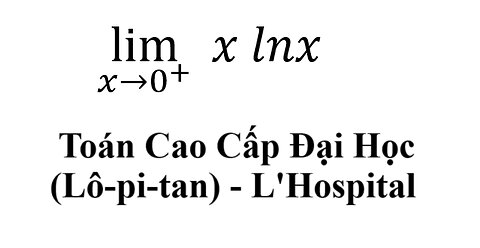
![Toán Cao Cấp Đại Học - MT1003 Giải tích 1 - Đại học Bách Khoa TPHCM- Cho hàm số f khả vi trên [8,21]](https://1a-1791.com/video/s8/1/T/A/8/V/TA8Vt.oq1b-small-Ton-Cao-Cp-i-Hc-MT1003-Gii-.jpg)
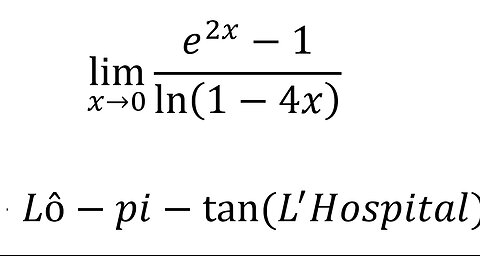




![Toán Đại Học: Chứng minh rằng ma trận [a b, c d] thỏa X^2 -(a+d)X + (ad-bc)I2=0](https://1a-1791.com/video/s8/1/f/a/r/Q/farQt.so1b.2-small-Ton-i-Hc-Chng-minh-rng-ma-t.jpg)


