Premium Only Content
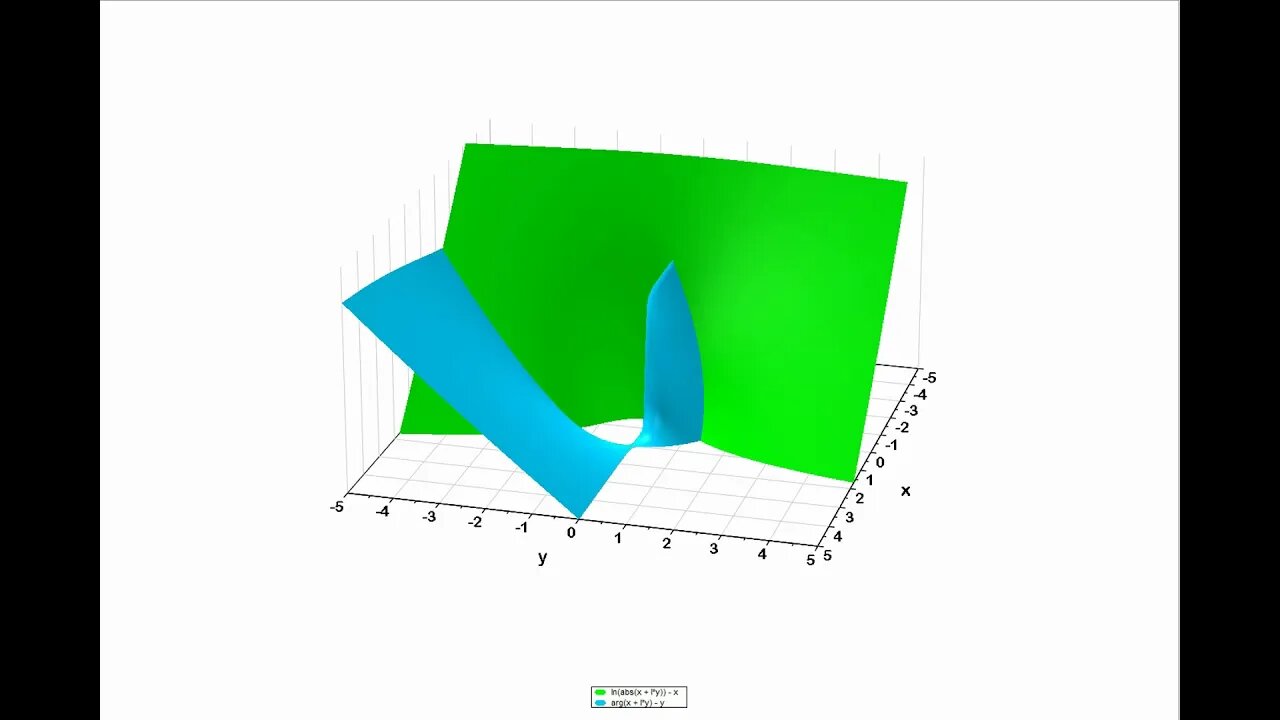
Fixpunkte der komplexen Logarithmusfunktion geometrisch bestimmt► Siehe Videobeschreibung
...
►Damit ein Fixpunkt vorliegt, muss gelten: f(z)=z also w=f(z)=z
► Zwei komplexe Zahlen sind genau dann gleich, wenn sie in Real- und Imaginärteil übereinstimmen. Es sind w und z also gleich, wenn ihre Realteile UND ihre Imaginärteile übereinstimmen.
► Der Realteil von z lautet x, der Imaginärteil lautet y.
(x bzw. y sind sozusagen Fixpunkt-Ebenen des Real- bzw. Imaginärteils).
► Der Realteil von w=lnz lautet ln|z|, der Imaginärteil lautet arg(z).
► Nun Realteile und Imaginärteile gleichsetzen: x=ln|z| bzw. y=arg(z)
► Beide Gleichungen umstellen: ln|z|-x=0 bzw. arg(z)-y=0
► Die Gleichungen fragen, wo die xy-Ebene geschnitten wird. Also zeichne ich die linken Seiten als Funktion und gucke, wo sich die beiden Funktionen untereinander und gleichzeitig mit der xy-Ebene schneiden. Dies ist an zwei Stellen der Fall, ungefähr bei 0.33+1.33i und 0.33-1.33i
-------------------------------------------
Kanalmitgliedschaft:
https://www.youtube.com/channel/UCiT0SUtIWTQZQd1galJ-hpw/join
Linklisten:
Es existieren viele Linklisten im Web, z.B. hier: http://www.mathematik.net
-
 43:27
43:27
barstoolsports
8 hours agoOld Dog Bites Back | Surviving Barstool S4 Ep. 9
71.8K2 -
 LIVE
LIVE
Right Side Broadcasting Network
7 days agoLIVE: TPUSA's America Fest Conference: Day One - 12/19/24
8,689 watching -
 LIVE
LIVE
Man in America
23 hours agoPfizer Has Been Caught RED HANDED w/ Dr. Chris Flowers
1,251 watching -

Slightly Offensive
6 hours ago $1.18 earnedAttempted ASSASSINATION of Nick J Fuentes LEAVES 1 DEAD! | Guest: Mel K & Breanna Morello
7.87K9 -
 1:43:08
1:43:08
Roseanne Barr
5 hours ago $2.96 earned"Ain't Nobody Good" with Jesse Lee Peterson | The Roseanne Barr Podcast #79
42.7K26 -

The StoneZONE with Roger Stone
2 hours agoTrump Should Sue Billionaire Governor JB Pritzker for Calling Him a Rapist | The StoneZONE
31.1K3 -
 LIVE
LIVE
Flyover Conservatives
21 hours agoAmerica’s Psychiatrist Speaks Out: Are We Greenlighting Violence? - Dr. Carole Lieberman | FOC Show
638 watching -
 LIVE
LIVE
LittleSaltyBear
4 hours ago $0.32 earnedNecromancing Path of Exile 2 4K
330 watching -
 3:51:34
3:51:34
Akademiks
4 hours agoJay Z War against Diddy Accuser Lawyer GOES CRAZY! Lil Baby Speaks OUT! Cardi v Offset? Bhad Bhabie?
73.9K5 -
 1:15:42
1:15:42
Josh Pate's College Football Show
5 hours ago $0.16 earnedCFP Changes Coming | Transfer Portal Intel | Games Of The Year | Head Coaches Set To Elevate
21.4K