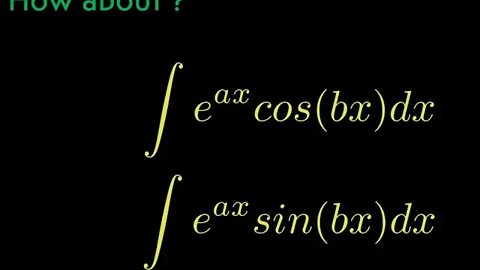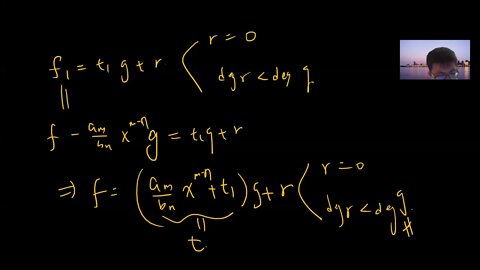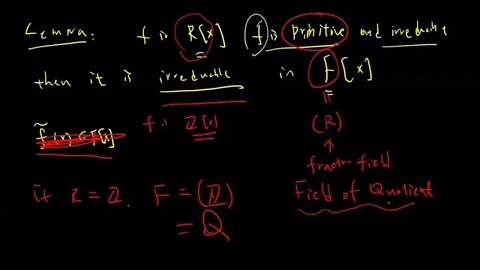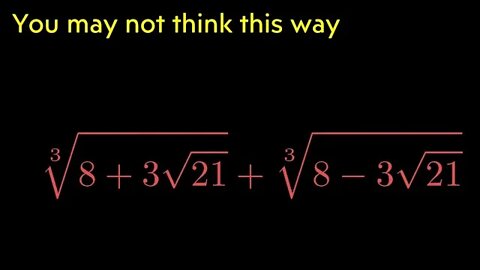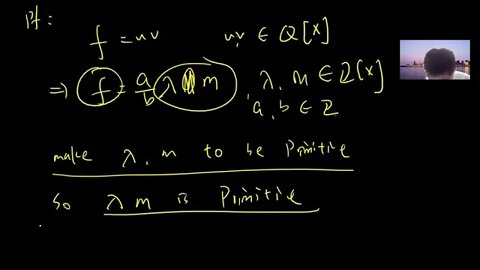All Videos
Selecting Integration Techniques Explained, List of Methods - Calculus
DrOfEng
How to Add and Subtract Polynomial Functions | (f+g)(x), (f+g)(3), (f-g)(x), and (f-g)(-2)
Minute Math
How to Evaluate a Polynomial Function for a Given Value | Minute Math
Minute Math
Solving Inequalities Interval Notation, Number Line, Absolute Value, Fractions & Variables - Algebra
TheOrganicChemistryTutor
Domain and Combinations of Functions
Math Videos
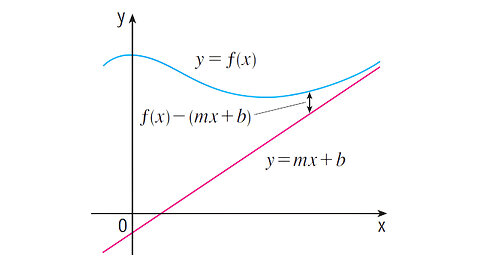
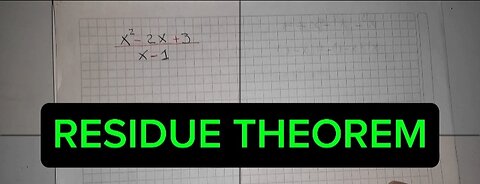
Integral of e^ax cos(bx) and Integral of e^ax sin(bx) no integration by part
ericntunctu
Tackle Your Algebra Assignments with Confidence! Expert Help Available Now
collegetaskhelp01
Client Work (Exam) | MATH 3213 Midterm test | Macroeconomic Theory II | University of New Brunswick
Assignment Helper
Hermitian matrix is diagonalizable and orthonormal basis
ericntunctu
Polynomial over a commutative ring
ericntunctu
Goldbach's theorem: Fermat numbers are coprime
ericntunctu
Permutation group (Symmetric group)
ericntunctu
The existence proof of eigenvectors and eigenvalues
ericntunctu
Prove Method of infinite Descent : square k is irrational if k is not square free
ericntunctu
Prove Method of infinite Descent (Vieta's jumping) : (4a^2-1)^2/(4ab-1) is integer, then a=b
ericntunctu