Premium Only Content
Parametric Curve, Arc Length Formula, Integral, Visual Proof, Practice Problems - Calculus
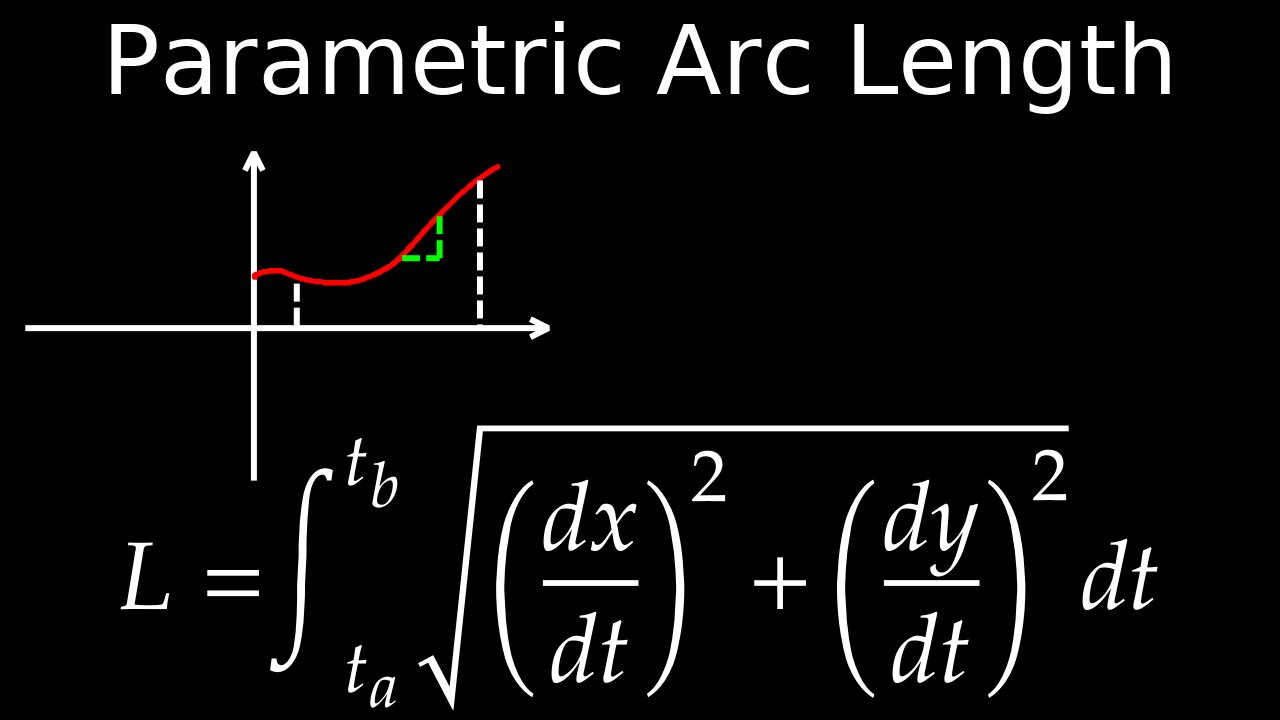
The arc length (\(L\)) of a parametric curve given by \(x(t)\) and \(y(t)\) for \(t\) from \(a\) to \(b\) is found by integrating the square root of the sum of the squares of the derivatives of the x and y components with respect to \(t\), from \(a\) to \(b\), using the formula: \(L=\int _{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\,dt\).
💡Here's how to calculate the arc length:
• Find the derivatives: of the parametric equations with respect to \(t\). Let \(x^{\prime }(t)=\frac{dx}{dt}\) and \(y^{\prime }(t)=\frac{dy}{dt}\).
• Square the derivatives: and add them together: \((x^{\prime }(t))^{2}+(y^{\prime }(t))^{2}\).
• Take the square root: of this sum: \(\sqrt{(x^{\prime }(t))^{2}+(y^{\prime }(t))^{2}}\).
• Integrate: the result with respect to \(t\) over the given interval, from \(a\) to \(b\).
💡Example:
Consider the parametric curve \(x(t)=t^{2}\) and \(y(t)=t^{3}\) for \(t\) from \(0\) to \(1\).
• Derivatives: \(\frac{dx}{dt}=2t\) and \(\frac{dy}{dt}=3t^{2}\).
• Square and add: \((2t)^{2}+(3t^{2})^{2}=4t^{2}+9t^{4}\).
• Integrate: \(L=\int _{0}^{1}\sqrt{4t^{2}+9t^{4}}\,dt=\int _{0}^{1}t\sqrt{4+9t^{2}}\,dt\).
Using a u-substitution (\(u=4+9t^{2}\)), the integral evaluates to \(\frac{1}{27}(13\sqrt{13}-8)\).
💡Why use this formula?
• It is derived from the Pythagorean theorem, where a small segment of the curve \(\Delta L\) is approximated by the hypotenuse of a small right triangle with sides \(\Delta x\) and \(\Delta y\). As \(\Delta t\rightarrow 0\), this becomes \(dL=\sqrt{(dx)^{2}+(dy)^{2}}\).
The arc length integral sums up these infinitesimal lengths to find the total length of the curve.
• It is especially useful for curves that cannot be easily expressed as a function of \(y\) in terms of \(x\), such as spirals.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1tolpJ9mIz-hrSc3BJyC0piUzPQ8cKD3b/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1tiM6iM6LTV0bkAhLvC8ij3bjvbloV5Jj/view?usp=drive_link
💡Chapters:
00:00 Parametric arc length integral
01:56 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 1:01:48
1:01:48
Benny Johnson
2 hours agoHow To Fix The Biggest Crisis In America: Housing | Saving The American Dream for Young People 🇺🇸
25.9K37 -
 LIVE
LIVE
LFA TV
14 hours agoLIVE & BREAKING NEWS! | FRIDAY 11/21/25
2,025 watching -
 2:44:29
2:44:29
Matt Kohrs
12 hours agoMarkets Tilted, OPEX Chaos & Payday Friday || Live Trading
18.7K1 -
 33:34
33:34
Rethinking the Dollar
1 hour agoFed Blinked Under Pressure: What Happens Next? | Friday News Update
3.58K -
 1:41:58
1:41:58
Graham Allen
3 hours agoTrump: “SEDITIOUS BEHAVIOR, punishable by DEATH!” Dems LOSING It!
122K851 -
 2:03:46
2:03:46
Badlands Media
11 hours agoBadlands Daily Nov. 21, 2025
37.8K7 -
 2:59:01
2:59:01
Wendy Bell Radio
7 hours agoOh HELL NO
60.4K78 -
 LIVE
LIVE
Major League Fishing
8 days agoLIVE! - Fishing Clash Team Series: Summit Cup - Day 6
159 watching -
 LIVE
LIVE
Caleb Hammer
4 hours agoThe Most Hated Person In Financial Audit History
123 watching -

The Big Mig™
3 hours agoTraitors Committing Sedition Says President Trump
1.49K9