Premium Only Content
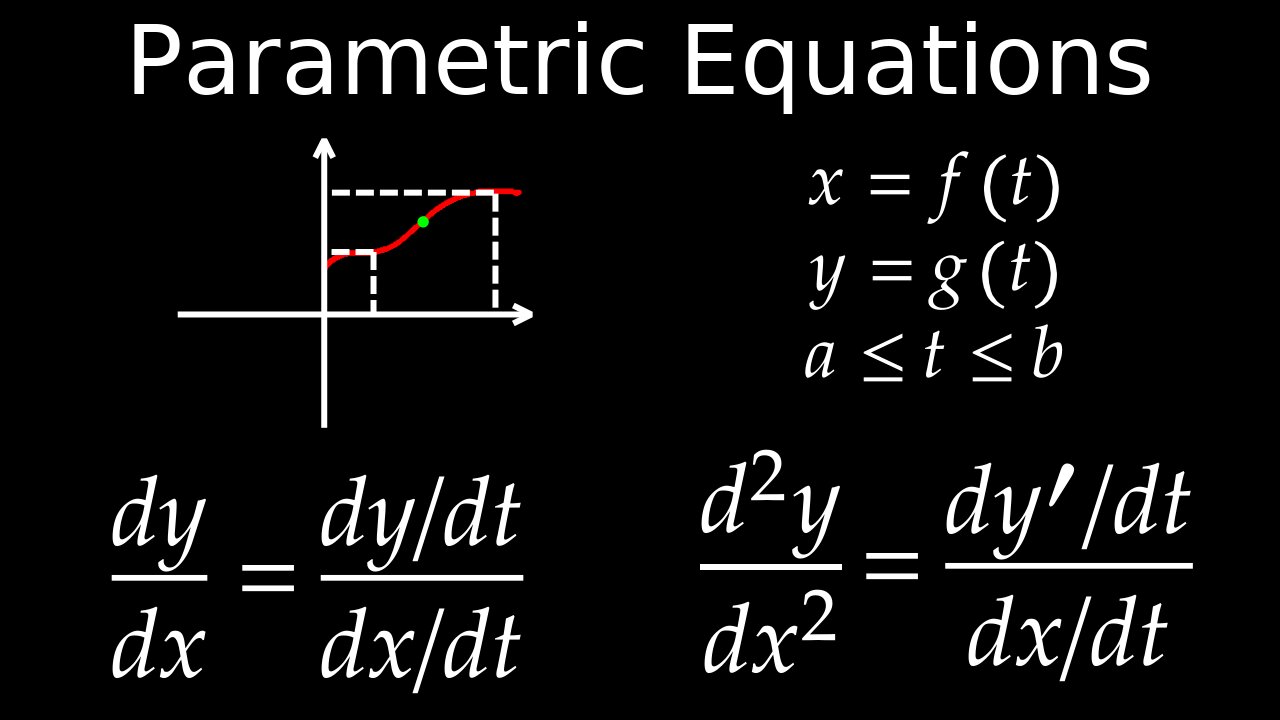
Parametric Equations, Curves, Definition, Differentiation, Worked example - Calculus
Parametric differentiation finds the derivative \(\frac{dy}{dx}\) when both \(x\) and \(y\) are functions of a third variable (the parameter, often \(t\)) by using the formula \(\frac{dy}{dx}=\frac{dy/dt}{dx/dt}\). To perform it, you differentiate both \(x\) and \(y\) with respect to the parameter (\(t\)) and then divide the resulting derivatives to find the desired derivative \(\frac{dy}{dx}\).
💡Steps for Parametric Differentiation
• Identify the parametric equations: You will have two equations, one for \(x\) and one for \(y\), both in terms of a parameter, say \(t\).
• Differentiate \(x\) with respect to \(t\): Find \(\frac{dx}{dt}\).
Differentiate \(y\) with respect to \(t\): Find \(\frac{dy}{dt}\).
• Apply the formula: Divide the derivative of \(y\) by the derivative of \(x\) to find \(\frac{dy}{dx}\):
\(\frac{dy}{dx}=\frac{dy/dt}{dx/dt}\) This works because, by the chain rule, \(\frac{dy}{dt}=\frac{dy}{dx}\cdot \frac{dx}{dt}\), so \(\frac{dy}{dx}=\frac{dy/dt}{dx/dt}\).
💡Example
Given the parametric equations: x = t^3 + t and y = t^2 + 1.
• Differentiate \(x\) and \(y\) with respect to \(t\):
\(\frac{dx}{dt}=3t^{2}+1\)
\(\frac{dy}{dt}=2t\)
• Apply the formula: \(\frac{dy}{dx}=\frac{2t}{3t^{2}+1}\)
💡Why use it?
Parametric differentiation is useful for analyzing complex curves in fields like computer graphics, physics, and engineering, as it allows for the description and analysis of intricate curves that might be difficult to represent explicitly or implicitly.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1tolpJ9mIz-hrSc3BJyC0piUzPQ8cKD3b/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1tiM6iM6LTV0bkAhLvC8ij3bjvbloV5Jj/view?usp=drive_link
💡Chapters:
00:00 Parametric equations and differentiation, with examples
03:39 Second derivative, with example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 2:24:29
2:24:29
The Culture War with Tim Pool
3 hours agoMAGA Civil War, Identity Politics, Christianity, & the Woke Right DEBATE | The Culture War Podcast
155K96 -
 LIVE
LIVE
Side Scrollers Podcast
2 hours agoVoice Actor VIRTUE SIGNAL at Award Show + Craig’s HORRIBLE Take + More | Side Scrollers
654 watching -
 1:59:21
1:59:21
The Charlie Kirk Show
2 hours agoCreeping Islamization + What Is An American? + AMA | Sedra, Hammer | 11.21.2025
24.7K16 -

Sean Unpaved
2 hours agoWill Caleb Williams & Bears WIN The NFC North? | UNPAVED
3.08K -
 LIVE
LIVE
Lara Logan
3 hours agoSTOLEN ELECTIONS with Gary Berntsen & Ralph Pezzullo | Ep 45 | Going Rogue with Lara Logan
409 watching -
 1:47:18
1:47:18
Steven Crowder
4 hours agoTo Execute or Not to Execute: Trump Flips the Dems Sedition Playbook Back at Them
246K259 -
 16:11
16:11
RealMetatron
19 hours agoHasan Piker got HUMBLED in New York
7.43K5 -
 LIVE
LIVE
Viss
3 hours ago🔴LIVE - Helping Those That Need It Today - Arc Raiders!
155 watching -
 43:37
43:37
The Rubin Report
3 hours agoTriggernometry Hosts Try to Hide Their Shock at Sam Harris’ Charlie Kirk Claim
29.7K28 -
 LIVE
LIVE
SOLTEKGG
2 hours ago🟢 Live: Pro Player Returns to Battlefield 6 RED SEC
45 watching