Premium Only Content
Volume with Cylindrical Shells Method, Integration, Formula, Examples, Problems - Calculus
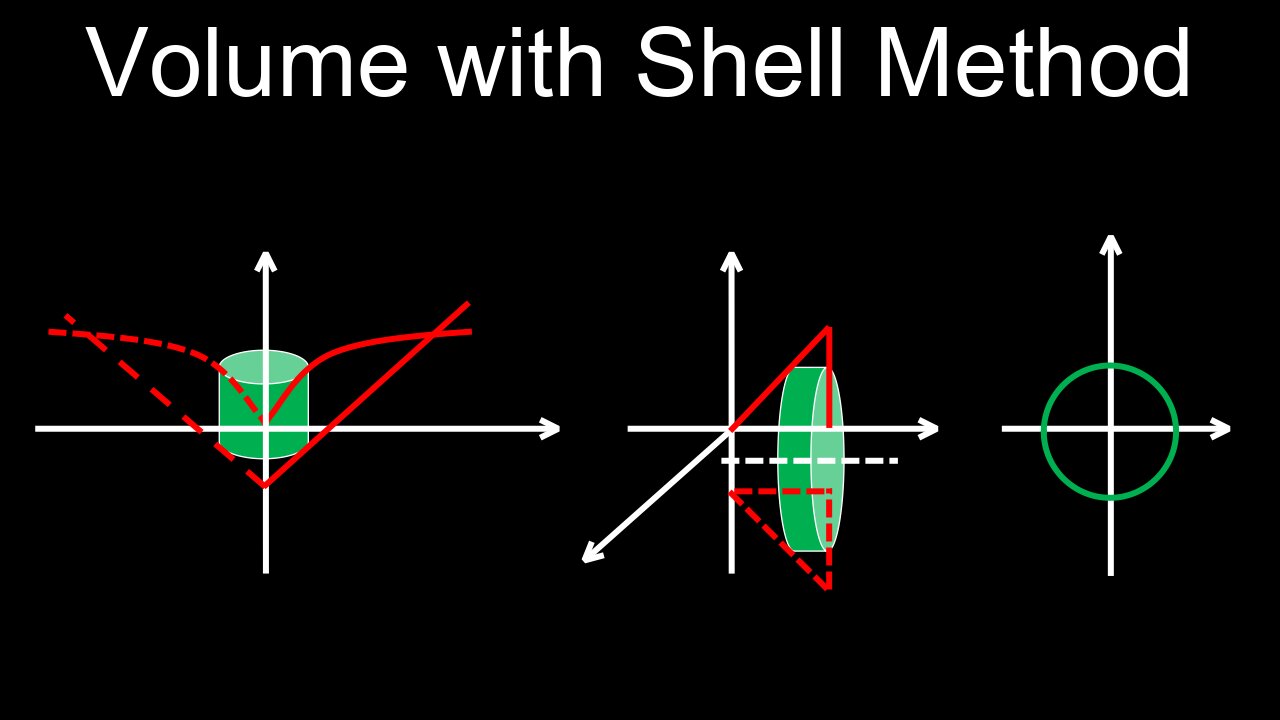
The "volume with shells" method, also known as the shell method, calculates the volume of a solid of revolution by integrating the volume of infinitesimally thin cylindrical shells. The formula is \(V=\int _{a}^{b}2\pi rh\,dx\) (for vertical rotation) or \(V=\int _{a}^{b}2\pi rh\,dy\) (for horizontal rotation), where \(r\) is the radius, \(h\) is the height of the shell, and \(dx\) or \(dy\) is the thickness. This method is often easier to use than the disk/washer method when the axis of rotation is perpendicular to the axis of the representative rectangle.
💡How to use the shell method
• Visualize the solid: Imagine a region in the plane. When you revolve it around an axis, it forms a 3D solid. The shell method views this solid as being made of many thin cylindrical "shells" stacked together.
• Determine the axis of rotation:
⚬ If rotating around a vertical axis (like the y-axis), you will integrate with respect to \(x\). The radius and height will be functions of \(x\).
⚬ If rotating around a horizontal axis (like the x-axis), you will integrate with respect to \(y\). The radius and height will be functions of \(y\).
• Define the radius (\(r\)) and height (\(h\)):
⚬ Radius (\(r\)): This is the distance from the axis of rotation to the representative rectangle.
⚬ Height (\(h\)): This is the length of the representative rectangle, which is usually a function of the variable of integration. When revolving two functions, the height is the top function minus the bottom function (for vertical rotation) or the rightmost function minus the leftmost function (for horizontal rotation).
• Set up the integral: Use the formula, which is the integral of the volume of a single shell (\(2\pi rh\,dx\) or \(2\pi rh\,dy\)) from the lower limit (\(a\)) to the upper limit (\(b\)) of your region.
⚬ Vertical axis rotation: \(V=\int _{a}^{b}2\pi xf(x)\,dx\), where \(x\) is the radius and \(f(x)\) is the height.
⚬ Horizontal axis rotation: \(V=\int _{a}^{b}2\pi yf(y)\,dy\).
• Solve the integral: Calculate the definite integral to find the total volume.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1GQtYzPXeZpvnm7EdpOAPfEyr-VSltAse/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1urkbDfPaDPsymE8T58TZZJHgeUw-P-qx/view?usp=drive_link
💡Chapters:
00:00 Volume with the cylindrical shell method
01:26 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-

Badlands Media
11 hours agoDEFCON ZERQ Ep. 018
135K42 -
 2:05:03
2:05:03
Inverted World Live
5 hours agoHouse Votes to Release Epstein Files w/ Emilie Hagen & Denise Bovee | Ep. 143
49.5K2 -
 3:02:27
3:02:27
TimcastIRL
5 hours agoEpstein Transparency PASSED UNANIMOUSLY, Trump To SIGN Release | Timcast IRL
225K109 -
 6:26:43
6:26:43
SpartakusLIVE
7 hours agoARC is SO ADDICTING - I just CAN'T stop || NEW SCHEDULE, NEED SLEEP
73.7K1 -
 LIVE
LIVE
Drew Hernandez
22 hours agoEPSTEIN TRANSPARENCY ACT PASSES: POLITICAL THEATER OR FULL DISCLOSURE?
1,072 watching -
 LIVE
LIVE
StevieTLIVE
5 hours ago#1 SOLO Warzone POV 6.9 KD
126 watching -
 2:57:53
2:57:53
Barry Cunningham
9 hours agoBREAKING NEWS: PRESIDENT TRUMP HOSTS DINNER WITH SAUDI ARABIA CROWN PRINCE MOHAMMED BIN SOLMAN !
71.6K27 -
 LIVE
LIVE
Spartan
4 hours agoPro Halo Player, insta locking Neon, plays Valorant for the first time since Beta. Rusty af on MnK
423 watching -
 30:14
30:14
Robbi On The Record
11 days ago $8.92 earnedYou’re Out of Alignment: Spiritually, Mentally, Physically. Here’s Why. ft Dr. Rich
67.6K5 -
 57:56
57:56
Sarah Westall
4 hours agoFormer DIA Chief of Global Operations: CIA and FBI - Broad Institutional Crisis w/ Jeffrey Prather
28.7K2