Premium Only Content
Arc Length Integral Formula, Distance, Problems and Solutions - Calculus
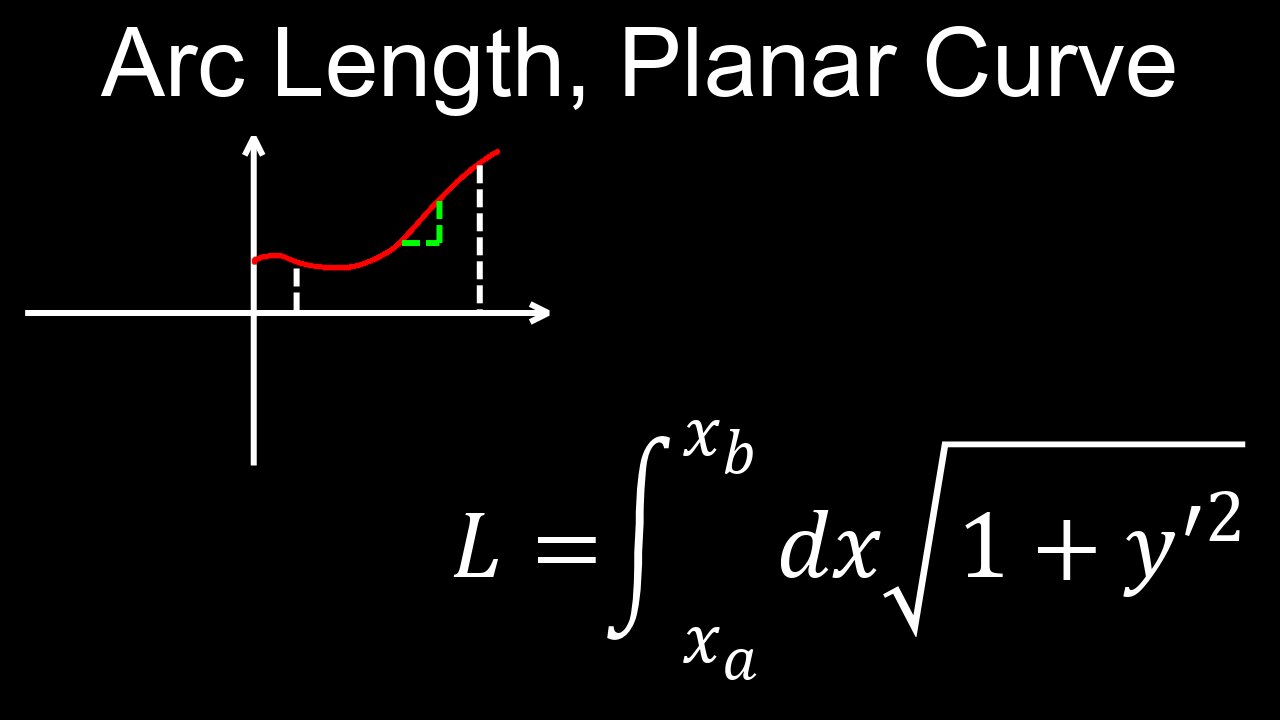
In calculus, arc length is the length of a curve between two points, calculated by integrating a formula that sums infinitesimal segments of the curve. For a smooth function \(y=f(x)\) over an interval \([a,b]\), the arc length \(L\) is found by integrating the square root of \((1+[f^{\prime }(x)]^{2})\) with respect to \(x\) from \(a\) to \(b\): \(L=\int _{a}^{b}\sqrt{1+[f^{\prime }(x)]^{2}}\,dx\).
💡Deriving the Arc Length Formula
The formula is derived by approximating the curve with a series of tiny line segments and finding the limit as the number of segments approaches infinity.
• Divide the curve: into \(n\) small segments.
• Approximate the length: of each segment with the hypotenuse of a right triangle, where the legs are the change in \(x\) (\(\Delta x\)) and the change in \(y\) (\(\Delta y\)).
• Use the Pythagorean theorem: The length of each segment is \(\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}\).
• Rewrite: this in terms of the derivative \(\frac{dy}{dx}\):
\(\sqrt{(\Delta x)^{2}(1+(\frac{\Delta y}{\Delta x})^{2})}=\Delta x\sqrt{1+(\frac{dy}{dx})^{2}}\).
• Sum the lengths: of all these segments to approximate the total arc length:
\(\sum \Delta x\sqrt{1+(\frac{dy}{dx})^{2}}\).
• Take the limit: as \(\Delta x\) approaches 0, transforming the sum into a definite integral:
\(\int _{a}^{b}\sqrt{1+(\frac{dy}{dx})^{2}}\,dx\).
💡Formulas for Different Cases
• For \(y=f(x)\): If the curve is defined as a function of \(x\), the arc length \(L\) from \(x=a\) to \(x=b\) is:
\(L=\int _{a}^{b}\sqrt{1+\left(\frac{dy}{dx}\right)^{2}}\,dx\quad \text{or}\quad L=\int _{a}^{b}\sqrt{1+[f^{\prime }(x)]^{2}}\,dx\).
For \(x=g(y)\): If the curve is defined as a function of \(y\), the arc length \(L\) from \(y=c\) to \(y=d\) is:
\(L=\int _{c}^{d}\sqrt{1+\left(\frac{dx}{dy}\right)^{2}}\,dy\quad \text{or}\quad L=\int _{c}^{d}\sqrt{1+[g^{\prime }(y)]^{2}}\,dy\).
• For Parametric Curves: For a curve defined by parametric equations \(x=x(t)\) and \(y=y(t)\), the arc length \(L\) from \(t=a\) to \(t=b\) is:
\(L=\int _{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}}\,dt\).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1GQtYzPXeZpvnm7EdpOAPfEyr-VSltAse/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1urkbDfPaDPsymE8T58TZZJHgeUw-P-qx/view?usp=drive_link
💡Chapters:
00:00 Arc length integral
02:04 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 LIVE
LIVE
The Bubba Army
22 hours agoMAJORIE TAYLOR GREENE QUITS! - Bubba the Love Sponge® Show | 11/25/25
1,488 watching -
 51:11
51:11
ZeeeMedia
15 hours agoBREAKTHROUGH: Nattokinase Dissolves 84% of Amyloid Microclots Within 2 Hours | Daily Pulse Ep 150
31K25 -
 1:12:22
1:12:22
Coin Stories with Natalie Brunell
22 hours agoArnaud Bertrand on Changing World Order: U.S. vs China, Gold, Bitcoin & Dollar Hegemony
19.5K7 -
 40:23
40:23
MetatronHistory
1 day agoI REFUSE To Use BCE/CE And Here is Why
8.07K9 -
 16:00
16:00
Actual Justice Warrior
2 days agoDearborn Muslims Go To WAR With Protesters
11.6K35 -
 16:33
16:33
Code Blue Cam
4 days agoWhen Begging for No Ticket Backfires Immediately
17K21 -
 19:22
19:22
stateofdaniel
4 days agoPresident Trump STRIKES Back Against Democrats Who Encouraged Military to DEFY Him
18.4K10 -
 14:12
14:12
itsSeanDaniel
1 day agoThe Dumbest Liberal in Congress Just EMBARRASSED Herself
17.7K11 -
 1:57:56
1:57:56
MG Show
20 hours agoTrump and Mamdani's Surprisingly Cordial Meeting; Trump Posts Q Memes
26.7K16 -
 1:10:51
1:10:51
MetatronGaming
1 day agoBroken Lore Don't Watch Full Game
54.7K2