Premium Only Content
Volume with the Washer Method, Formula, Examples, Practice Problems - Calculus
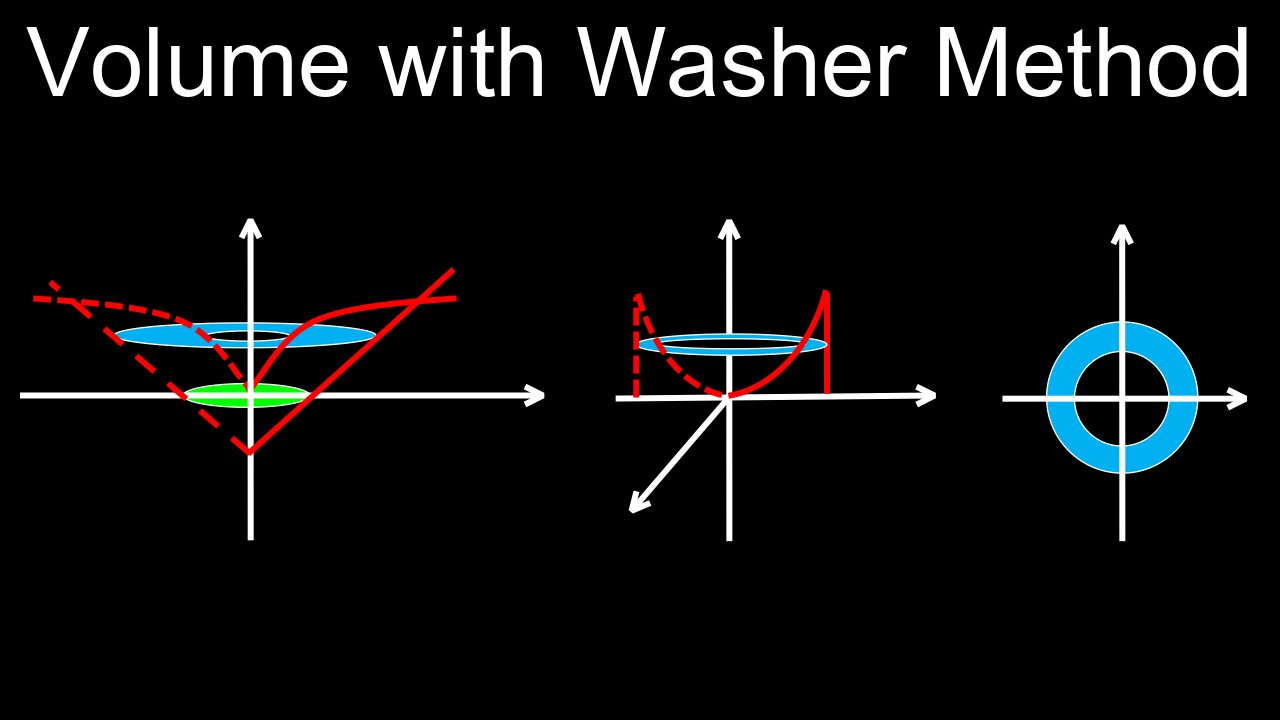
The washer method calculates the volume of a solid of revolution with a hole by integrating the area of its "washers" (hollow discs). The volume of a single washer is found by subtracting the volume of the inner cylinder from the outer one, which is equivalent to \(\pi (R^{2}-r^{2})\Delta x\), where \(R\) is the outer radius, \(r\) is the inner radius, and \(\Delta x\) is the thickness. To find the total volume, you set up and solve a definite integral using this formula, where the limits of integration are determined by the intersection points of the functions bounding the region.
💡Steps for using the washer method
• Sketch the region: Draw the region between the two functions and identify the axis of rotation.
• Determine the representative rectangle: Draw a small, representative rectangle that is perpendicular to the axis of rotation. This rectangle will form a washer when rotated.
⚬ If the rectangle is vertical (perpendicular to the x-axis), the thickness is \(dx\), and you will integrate with respect to \(x\).
⚬ If the rectangle is horizontal (perpendicular to the y-axis), the thickness is \(dy\), and you will integrate with respect to \(y\).
• Find the inner and outer radii (\(r\) and \(R\)):
⚬ Outer radius (\(R\)): The distance from the axis of rotation to the outer curve of the region.
⚬ Inner radius (\(r\)): The distance from the axis of rotation to the inner curve of the region.
⚬ This can be found by taking the "outer function" minus the "axis of rotation" (for vertical rectangles) or "right function" minus "axis of rotation" (for horizontal rectangles). Be sure both radii are expressed in terms of the same variable you are integrating with respect to.
• Set up the integral:
⚬ The formula for the volume of a single washer is \(dV=\pi (R^{2}-r^{2})dx\) or \(dV=\pi (R^{2}-r^{2})dy\).
⚬ The total volume is the integral of this expression over the appropriate interval: \(V=\int _{a}^{b}\pi (R(x)^{2}-r(x)^{2})dx\) or \(V=\int _{c}^{d}\pi (R(y)^{2}-r(y)^{2})dy\).
• Find the limits of integration: Determine the values of \(x\) or \(y\) where the inner and outer curves intersect to find the lower and upper bounds of your integral.
• Evaluate the integral: Solve the definite integral to find the numerical volume of the solid.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1GQtYzPXeZpvnm7EdpOAPfEyr-VSltAse/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1urkbDfPaDPsymE8T58TZZJHgeUw-P-qx/view?usp=drive_link
💡Chapters:
00:00 Volume with the washer method, revolve around x and y axes, with example
03:55 Washer method, revolve around other axes, with example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 1:41:58
1:41:58
Graham Allen
2 hours agoTrump: “SEDITIOUS BEHAVIOR, punishable by DEATH!” Dems LOSING It!
107K825 -
 LIVE
LIVE
Matt Kohrs
11 hours agoMarkets Tilted, OPEX Chaos & Payday Friday || Live Trading
693 watching -
 LIVE
LIVE
Badlands Media
9 hours agoBadlands Daily Nov. 21, 2025
3,457 watching -
 LIVE
LIVE
Wendy Bell Radio
6 hours agoOh HELL NO
7,341 watching -
 LIVE
LIVE
Major League Fishing
8 days agoLIVE! - Fishing Clash Team Series: Summit Cup - Day 6
193 watching -
 UPCOMING
UPCOMING
Caleb Hammer
2 hours agoThe Most Hated Person In Financial Audit History
621 -
 UPCOMING
UPCOMING
The Big Mig™
2 hours agoTraitors Committing Sedition Says President Trump
1654 -
 30:49
30:49
MetatronHistory
16 hours agoThe Truth about Women Warriors Based on Facts, Evidence and Sources
5K3 -
 15:17
15:17
IsaacButterfield
6 hours ago $0.44 earnedAustralia’s Most Hated Politician
4.62K3 -
 4:28
4:28
MudandMunitions
12 hours agoSHOT Show 2026 Is Locked In and I’m a Gundie Nominee!
3.27K