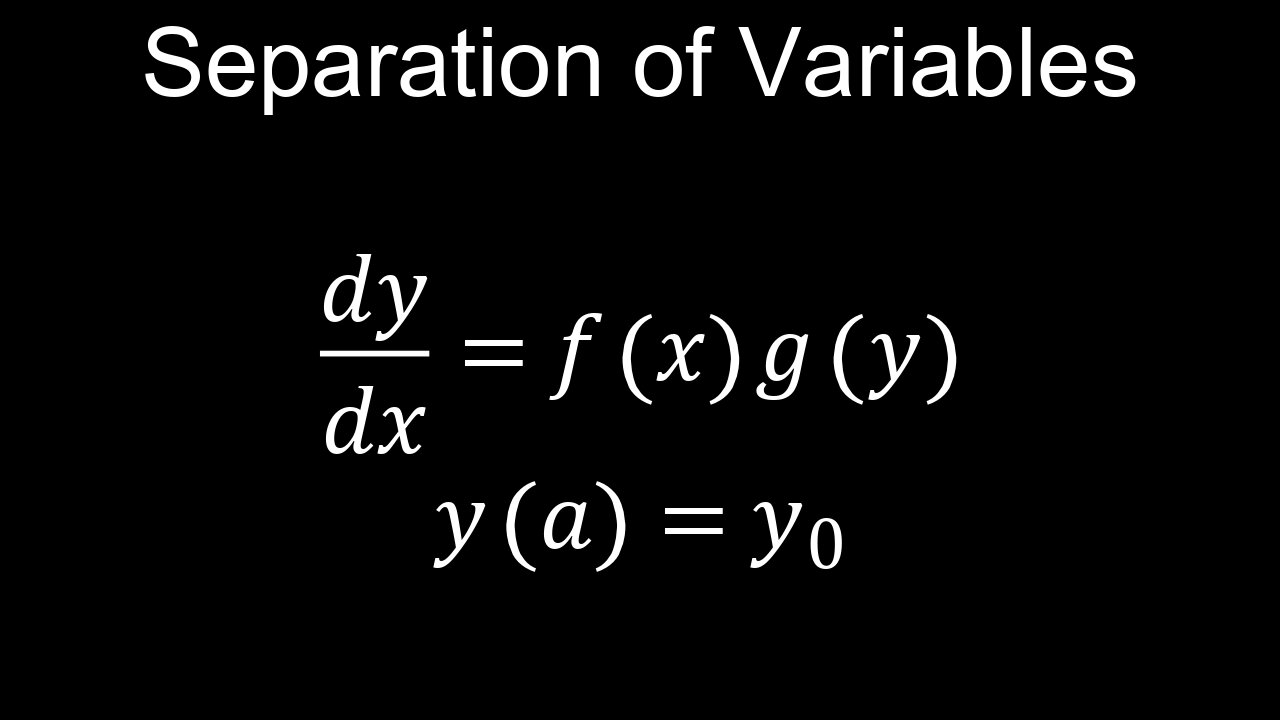
Separation of Variables Method, Differential Equations, Integration, Examples - Calculus

The separation of variables method is a mathematical technique for solving differential equations by algebraically rearranging them so that all terms involving one variable are on one side of the equation and all terms involving the other variable are on the opposite side. This separation allows each side of the equation to be integrated independently, leading to an equation without derivatives, which represents the solution to the original differential equation. The method is applicable to differential equations that can be expressed in a product form, such as dy/dx = g(x)h(y).

💡How it Works
• Rewrite the Equation: The first step is to rewrite the differential equation so that all terms containing the dependent variable (e.g., y and dy) are on one side, and all terms containing the independent variable (e.g., x and dx) are on the other. For example, if you have dy/dx = ky, you would rewrite it as dy/y = kdx.
• Integrate Both Sides: Once the variables are separated, integrate both sides of the equation. Remember to include a constant of integration on one side.
• Solve for the Variable: Simplify the integrated equation and, if possible, solve for the dependent variable to find the explicit solution.

💡Example
To solve the differential equation dy/dx = ky:
• Separate variables: Multiply by dx and divide by y to get dy/y = kdx.
• Integrate: Integrate both sides: ∫(1/y) dy = ∫k dx.
• Solve: This yields ln|y| + C₁ = kx + C₂, which simplifies to ln|y| = kx + C (where C = C₂ - C₁). Taking the exponential of both sides gives y = e^(kx+C) = Ae^(kx) (where A = e^C), which is the general solution.

💡Key Considerations
• Applicability: The method is only applicable if the differential equation can be expressed in a specific product form, like dy/dx = g(x)h(y).
• Implicit Solutions: It's not always possible to find an explicit solution; you may have to leave the solution in an implicit form.
• Singular Solutions: The method might miss certain singular solutions that don't fit the general form of the solution obtained.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1DMK4EA0f8SfF4SgdiOZ39F73He_YWIwe/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1QpzjiCPjfoxydzZqvjyJJsqv9jyRLZ0o/view?usp=drive_link

💡Chapters:
00:00 Separation of variables, general solution, with example
02:40 Particular solution, with examples

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://www.youtube.com/channel/UCJAvCW22EeE_2s2ZlJne7uQ?sub_confirmation=1
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng