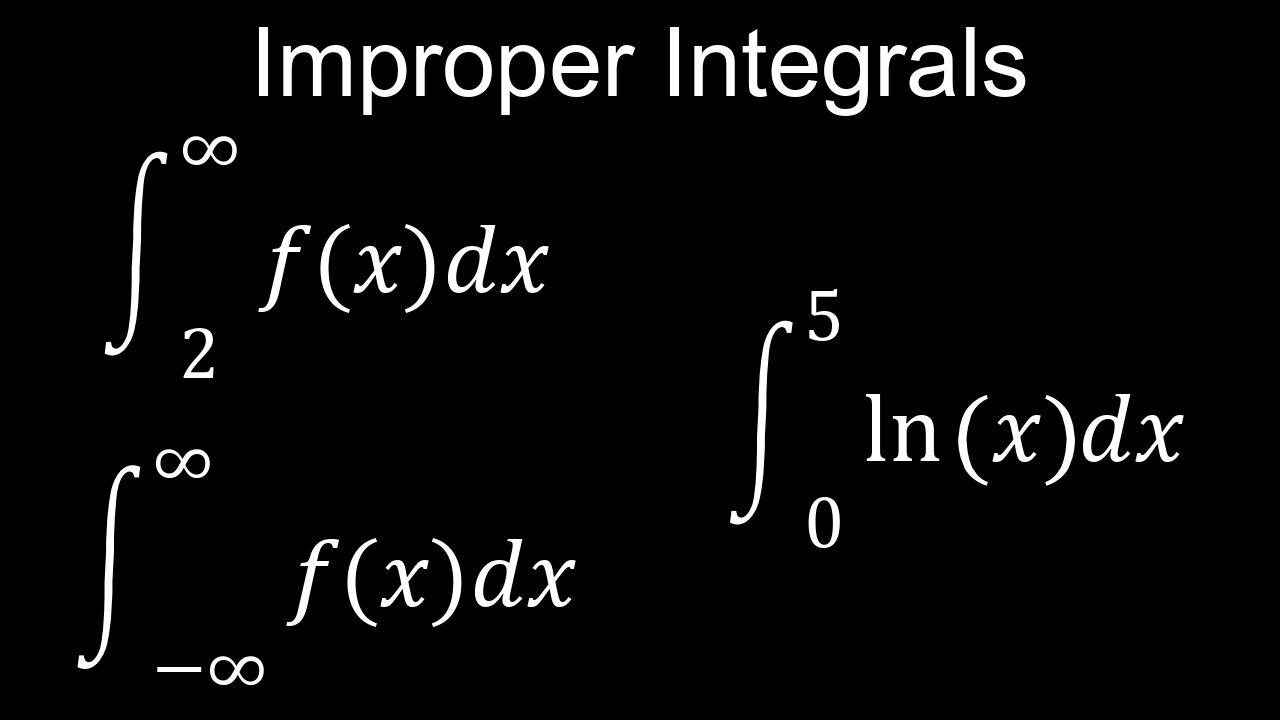
Improper Integrals, Type 1 and 2, Examples, Converge or Diverge, Practice Problems - Calculus

Improper integrals extend definite integrals to situations with an infinite integration interval or a function with a discontinuity within the interval. They are evaluated by replacing the problematic limit (infinity or a discontinuity) with a variable, say 't', and then calculating the definite integral from that variable to the other limit. The key is to take the limit as the variable 't' approaches the infinite or problematic value. If the limit results in a finite number, the integral converges; if the limit does not exist or is infinite, the integral diverges.

💡Two Types of Improper Integrals
• Type 1: Infinite Limits of Integration
∘Description: This type involves integrating over an interval that extends to infinity, such as from a finite number to positive or negative infinity, or between two infinite limits.
∘Example: The integral of 1/x² from 1 to infinity: ∫₁^∞ (1/x²) dx.
∘Evaluation:
⬩Replace the infinite limit with a variable (e.g., 'b'): lim (b→∞) ∫₁^b (1/x²) dx.
⬩Evaluate the definite integral: ∫₁^b (1/x²) dx = [-1/x]₁^b = -1/b - (-1/1) = 1 - 1/b.
⬩Take the limit as 'b' approaches infinity: lim (b→∞) (1 - 1/b) = 1.
⬩Conclusion: Since the limit is a finite number (1), the integral converges.

• Type 2: Integrands with a Discontinuity
∘Description: This type of integral occurs when the function being integrated has a vertical asymptote or some other form of discontinuity within the interval of integration.
∘Example: The integral of 1/x from 0 to 1: ∫₀¹ (1/x) dx, where x=0 is a point of discontinuity.
∘Evaluation:
⬩The approach from the left for the discontinuity.
⬩Replace the problematic limit (0) with a variable (e.g., 'a') and take the limit: lim (a→0⁺) ∫ₐ¹ (1/x) dx.
⬩Evaluate the definite integral: ∫ₐ¹ (1/x) dx = [ln|x|]ₐ¹ = ln|1| - ln|a| = 0 - ln|a| = -ln|a|.
⬩Take the limit as 'a' approaches 0 from the right: lim (a→0⁺) (-ln|a|) = ∞.
⬩Conclusion: Since the limit is infinity, the integral diverges.

💡Convergence vs. Divergence
• Convergent: An improper integral is convergent if the limit of the corresponding definite integral exists and is a finite number.
• Divergent: An improper integral is divergent if the limit does not exist or is infinite.

By using limits, improper integrals allow us to determine if an unbounded area under a curve or an area with a discontinuity can be represented by a finite value.

💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link

💡Chapters:
00:00 Improper integrals
01:31 Worked example

🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng