Premium Only Content
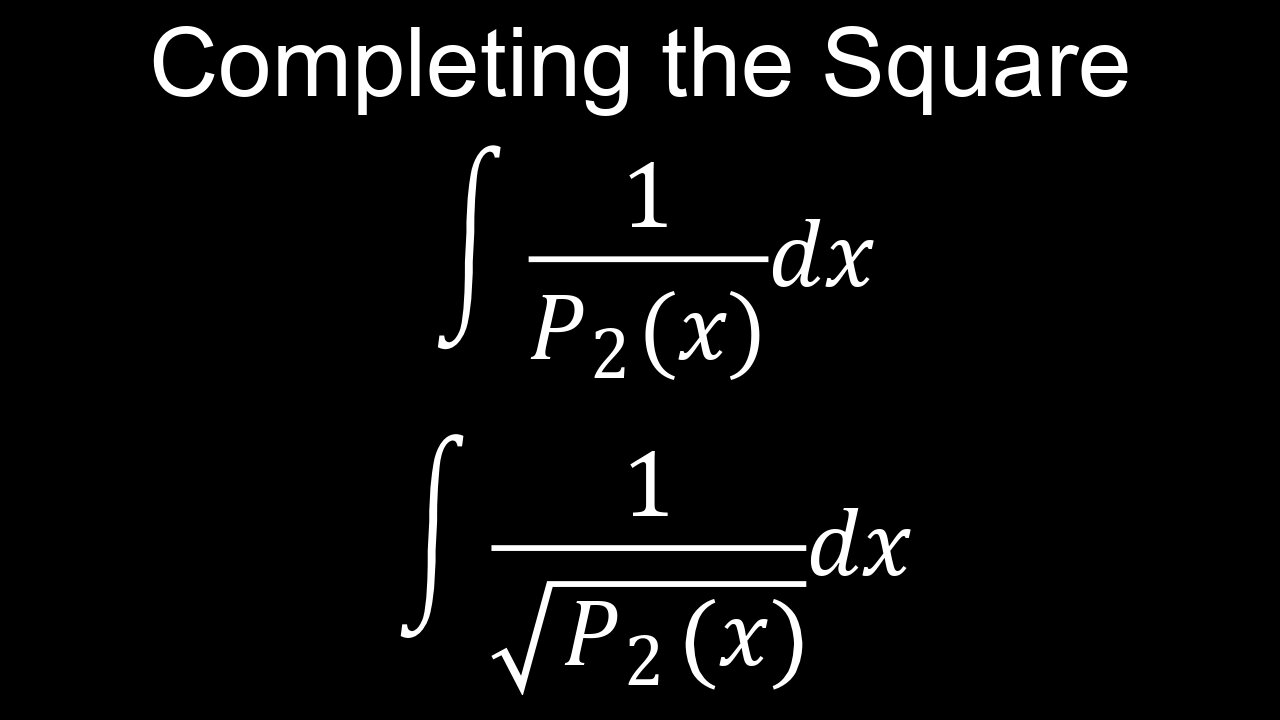
Integration, Completing the Square, Examples, Worksheet, Practice Problems - Calculus
Integration by completing the square is a method for evaluating integrals with quadratic expressions in the denominator, particularly when the quadratic is irreducible (cannot be factored into real linear terms). The process involves rewriting the quadratic \(ax^{2}+bx+c\) into the form \(a(x+k_{1})^{2}+k_{2}\), which is then manipulated using u-substitution into a standard integral form, typically involving the inverse tangent (\(\arctan \)) or inverse sine (\(\arcsin \)) functions.
💡Steps for Completing the Square
• Ensure x² coefficient is one: If the coefficient of \(x^{2}\) (let's call it \(a\)) is not 1, factor it out from the entire quadratic expression.
∘ For example, \(2x^{2}-4x+11\) becomes \(2(x^{2}-2x+\frac{11}{2})\).
• Complete the square on the remaining quadratic: Take the coefficient of the \(x\) term (let's call it \(b^{\prime }\)), divide it by 2, and then square the result. Add and subtract this value inside the parenthesis.
∘ For example, in \(x^{2}-2x+\frac{11}{2}\), the \(x\) coefficient is -2.
∘ Half of -2 is -1, and squaring it gives 1.
∘ The expression becomes \(2(x^{2}-2x+1+\frac{11}{2}-1)\).
• Factor the perfect square trinomial: The first three terms inside the parenthesis now form a perfect square trinomial, \((x+b^{\prime }/2)^{2}\).
∘ \(2((x-1)^{2}+\frac{9}{2})\).
• Simplify the constant term: Combine the remaining constant terms.
∘ \(2((x-1)^{2}+\frac{9}{2})=2(x-1)^{2}+9\).
💡Applying to Integrals
• Rewrite the denominator: Substitute the completed square form into the integral.
∘ For example, \(\int \frac{1}{2x^{2}-4x+11}dx\) becomes \(\int \frac{1}{2(x-1)^{2}+9}dx\).
• Use substitution: Let \(u\) be the term in the parenthesis. In the example, \(u=x-1\), so \(du=dx\).
∘ The integral becomes \(\int \frac{1}{2u^{2}+9}du\).
• Manipulate to match standard forms: Factor out constants and rearrange the expression to match a known integral, often involving the form \(\frac{1}{a^{2}+u^{2}}\).
∘ \(\int \frac{1}{2u^{2}+9}du=\frac{1}{2}\int \frac{1}{u^{2}+(3/\sqrt{2})^{2}}du\).
• Integrate: Apply the appropriate integral formula.
∘ The integral \(\int \frac{1}{a^{2}+x^{2}}dx=\frac{1}{a}\arctan (\frac{x}{a})+C\).
∘ The final result can be converted back to the original variable.
💡When to Use This Method
• Irreducible quadratics: This method is essential for integrals involving quadratic denominators that do not factor into real linear terms.
• Non-standard forms: It is useful for integrands that resemble natural logarithms or inverse trigonometric functions but are "off" due to the quadratic expression.
• Standard forms: Completing the square transforms a general quadratic into a form that can be solved using known integration techniques, such as those found in integral tables.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Completing the square
00:40 Worked example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 LIVE
LIVE
Barry Cunningham
2 hours agoPRESIDENT TRUMP EVENTS IN SOUTH KOREA | MIKE JOHNSON SHUTDOWN DAY 29 PRESSER | MORE NEWS!
1,591 watching -
 LIVE
LIVE
The HotSeat
29 minutes agoAmerican Politics Are Really NOT This HARD!!!!
326 watching -
 2:19:30
2:19:30
Side Scrollers Podcast
5 hours agoAngry Joe’s TDS/Halo Meltdown + Console War is OVER + Twitch Staff FIRED + More | Side Scrollers
34.7K9 -
 1:13:46
1:13:46
DeVory Darkins
3 hours agoDemocrat Voters get CRUSHING NEWS as Trump celebrates MAJOR TRADE DEAL
118K52 -
 14:54
14:54
The Kevin Trudeau Show Limitless
6 hours agoThe Hidden Force Running Your Life
2.9K4 -
 1:00:11
1:00:11
Mark Kaye
4 hours ago🔴 Joe Biden Autopen Scandal Update - Staff Paid MILLIONS To Keep Quiet!
13.7K4 -
 LIVE
LIVE
SternAmerican
1 day agoELECTION INTEGRITY CALL – WED, OCT 29 · 2 PM EST | FEATURING NEW JERSEY
103 watching -
 1:05:34
1:05:34
Timcast
4 hours agoDemocrats SUE, Trump USDA Says ITS DONE, No Food Stamps Will Come, Riots Feared
167K219 -
 1:59:16
1:59:16
The Charlie Kirk Show
4 hours agoProud to Be American? + VA and NJ + Charlie's Education Vision | Maloney, Arnn | 10.29.2025
62.4K12 -
 38:32
38:32
Code Blue Cam
4 hours agoHow Police Stopped a Potential Church Massacre...
16.2K4