Premium Only Content
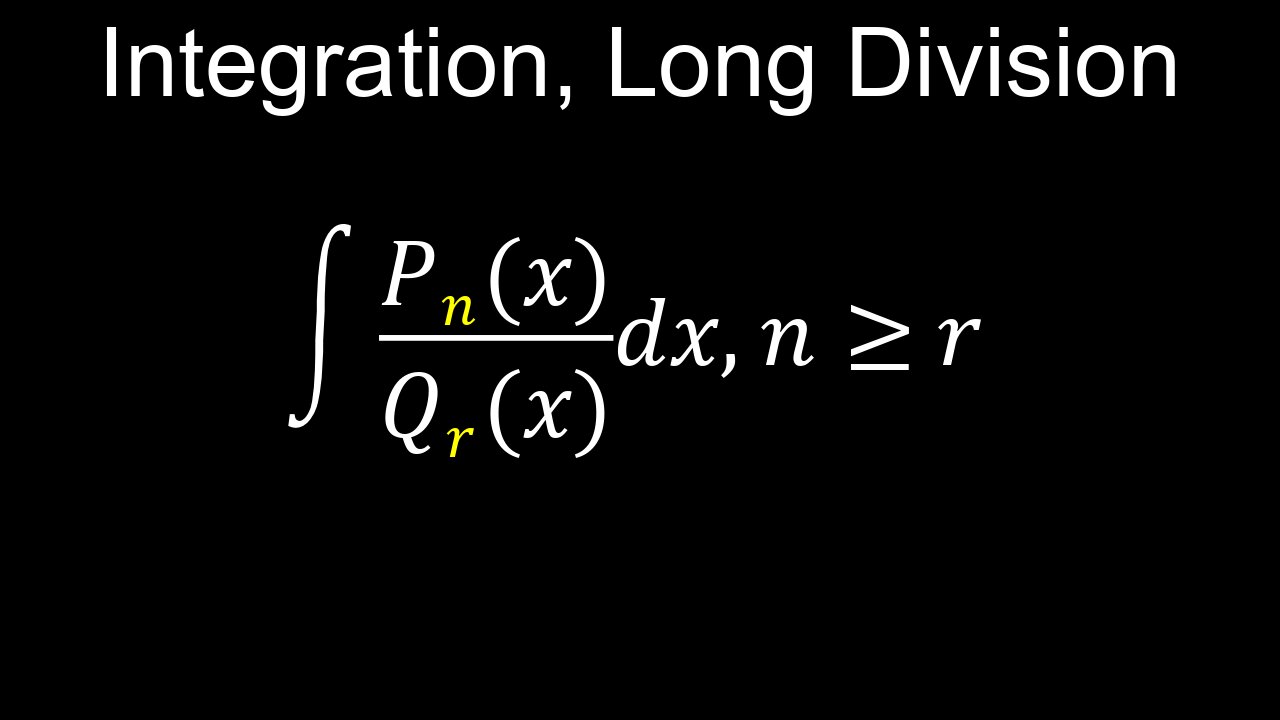
Integration, Polynomial Long Division Method, Example, Worksheet, Practice Questions - Calculus
Integration using long division is a technique to integrate improper rational functions, where the degree of the numerator is greater than or equal to the degree of the denominator. The process involves performing polynomial long division to rewrite the integrand as a polynomial plus a proper rational function (where the numerator's degree is less than the denominator's). The polynomial part is integrated directly using basic rules, while the proper rational function part is then integrated using other methods, such as partial fraction decomposition or completing the square.
💡When to Use Long Division for Integration
• Improper Rational Functions: Use this method when you're faced with an integral containing a rational expression (a fraction of polynomials) where the numerator's degree is greater than or equal to the denominator's degree.
💡Steps for Integration Using Long Division
• Perform Long Division: Divide the numerator by the denominator to find the quotient and remainder.
• Rewrite the Integrand: Express the original rational function as the quotient plus the remainder divided by the divisor.
∘ Original integrand = Quotient + (Remainder / Divisor)
• Integrate Term by Term: The integral can now be broken down into the integral of the polynomial (quotient) and the integral of the proper rational function (remainder/divisor).
∘ ∫ (Numerator/Denominator) dx = ∫ (Quotient) dx + ∫ (Remainder/Divisor) dx
• Integrate the Polynomial: The integral of the polynomial quotient is found using the power rule for integration.
• Integrate the Proper Rational Function: The remaining integral, which is now a proper rational function, can be integrated using techniques like:
• Partial Fraction Decomposition: If the denominator can be factored into simpler linear or irreducible quadratic factors.
• Completing the Square: If the denominator is an irreducible quadratic, completing the square can transform it into a form suitable for arctangent integrals or logarithmic forms.
• U-Substitution: U-substitution might be used to simplify the integral of the proper rational piece.
💡Example
To integrate ∫ (x³ + 3x² + 8x + 19) / (x² + 5) dx, you would first perform long division.
• Long Division: Divide x³ + 3x² + 8x + 19 by x² + 5, yielding a quotient of (x + 3) and a remainder of (3x + 4).
• Rewrite: The integral becomes ∫ (x + 3 + (3x + 4)/(x² + 5)) dx.
• Integrate:
∘∫ (x + 3) dx = x²/2 + 3x
∘∫ (3x / (x² + 5)) dx + ∫ (4 / (x² + 5)) dx
∘These remaining integrals are solved using u-substitution and arctangent integration, respectively, resulting in (3/2)ln(x² + 5) and (4/√5)arctan(x/√5).
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Integration by polynomial long division
01:02 Worked Example
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 1:54:42
1:54:42
The Quartering
2 hours agoFood Stamp Riots Are Coming, New Charlie Kirk Assassin Discord Messages Leak & Console Wars End!
133K48 -
 16:09
16:09
iCkEdMeL
3 hours ago🔴 LIVE: Tyler Robinson Pretrial Hearing in Charlie Kirk Assassination Case
15.8K3 -
 1:11:50
1:11:50
DeVory Darkins
4 hours agoDemocrats left scrambling after USDA issues NIGHTMARE Update
161K130 -
 21:05
21:05
Stephen Gardner
4 hours ago🔥Trump Drops NIGHTMARE NEWS for Democrats!!!
38.6K114 -
 LIVE
LIVE
Owen Shroyer
2 hours agoOwen Report - 10-27-2025 - Trump Secures Trade Deals Ahead Of Meeting With Xi
1,219 watching -
![[Ep 778] NYC Embraces Communism, Argentina Rejects It | Newsom Lies; As Always](https://1a-1791.com/video/fwe2/34/s8/1/w/y/k/u/wykuz.0kob-small-Ep-778-NYC-Embraces-Communi.jpg) LIVE
LIVE
The Nunn Report - w/ Dan Nunn
2 hours ago[Ep 778] NYC Embraces Communism, Argentina Rejects It | Newsom Lies; As Always
163 watching -
 1:09:36
1:09:36
Sean Unpaved
4 hours agoBrian Kelly's Boot From LSU, NFL Week 8 Snoozefest, & CFB's Week 9 Upset Rodeo
28.6K2 -
 1:04:35
1:04:35
Jeff Ahern
2 hours agoMonday Madness with Jeff Ahern
14.3K1 -
 1:03:58
1:03:58
Timcast
4 hours agoTrump DEPLOYS Election Monitors To Blue States, Democrats SCREAM RIGGED ELECTION
188K153 -
 2:07:27
2:07:27
Steven Crowder
7 hours agoWho Belongs: What the Future of the American Right Wing Looks Like
459K337