Premium Only Content
Accumulation of Change, Derivative Formula, Meaning, Worksheet, Problems - Calculus
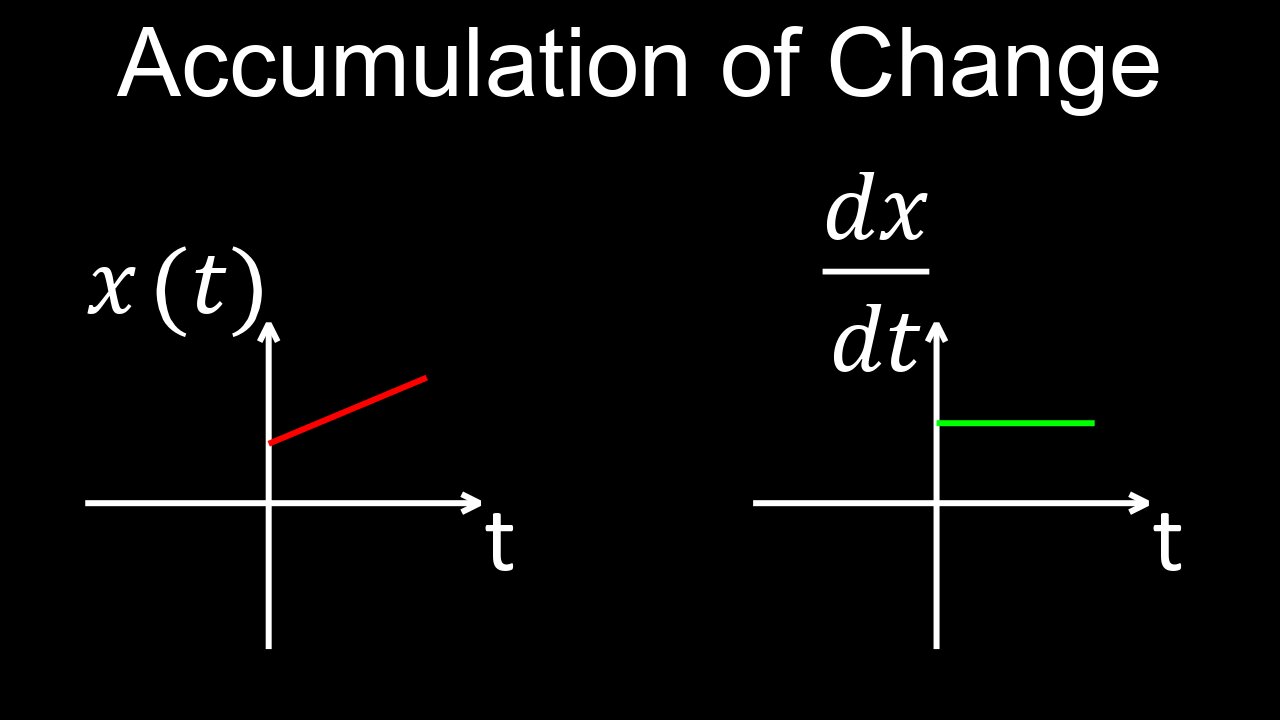
"Accumulation of change" is a fundamental calculus concept referring to the total change of a quantity over a specific interval, calculated by integrating its rate of change. For example, if you have the velocity of a car (the rate of change of position), the accumulated change in position (the total distance traveled or displacement) is found by integrating the velocity function over a given time period. This concept is represented graphically as the area under the curve of the rate function within the specified interval.
💡Key Aspects
• Rate of Change: Accumulation of change works with the rate at which a quantity changes.
• Integration: The mathematical operation used to find the accumulation of change is definite integration.
• Net Change: The result is the total, or net, change in the quantity over the interval.
• Graphical Representation: The definite integral of a rate function is equivalent to the area between the curve of that function and the x-axis over a specific interval.
💡Real-World Examples
• Distance Traveled: Integrating a car's velocity over time gives the total distance it has traveled.
• Water in a Tank: Integrating the rate of water flow into a tank gives the total volume of water accumulated over a period.
• Revenue Earned: Integrating the rate of daily earnings gives the total revenue over a week.
💡Distinction from Total Value
• The accumulation of change tells you how much a quantity has changed, but not its total value.
• To find the total value, you need a boundary value—the starting or ending value of the quantity at a specific point. You then add this boundary value to the accumulated change. For instance, if you know the initial amount of water in a tank and add the total water accumulated (from integration) to it, you get the final volume of water.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Accumulation of change from the rate function
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 2:10:12
2:10:12
Side Scrollers Podcast
17 hours agoMAJOR Hasan Allegations + Arc Raiders Review CONTROVERSY + Craig TRENDS on X + More | Side Scrollers
97.7K13 -
 9:24
9:24
MattMorseTV
14 hours ago $8.86 earnedFetterman is actually DOING IT...
8.29K33 -
 49:23
49:23
Live From The Casita
7 hours agoLive Music Jam
6.56K4 -
 2:55:50
2:55:50
The Pascal Show
12 hours ago $0.64 earnedMASSIVE CHAOS?! Transportation Secretary Hold Presser On Air Travel & More
4.18K2 -
 1:06:35
1:06:35
TruthStream with Joe and Scott
1 day agoZero Limits Round Table with Joe Vitale, Lisa Schermerhorn and more of the cast!
8.01K -
 LIVE
LIVE
Lofi Girl
2 years agoSynthwave Radio 🌌 - beats to chill/game to
173 watching -
 7:40
7:40
Blabbering Collector
13 hours agoLEAKED: Draco Malfoy, Hooch, Neville Longbottom! | Harry Potter HBO Show Update, Wizarding News
13K -
 3:06:35
3:06:35
Badlands Media
16 hours agoDEFCON ZERQ Ep. 017: Tesla Tech, Ancient Power & The Fight for Human Consciousness
233K59 -
 3:11:56
3:11:56
TimcastIRL
9 hours agoDOJ Launches FULL INVESTIGATION Into TPUSA Antifa RIOT, Media Says Mostly Peaceful | Timcast IRL
261K91 -
 3:16:27
3:16:27
Barry Cunningham
12 hours agoBREAKING NEWS: SOLVING THE HOUSING CRISIS BY UNDERSTANDING VETERANS DAY! AND IT'S MOVIE NIGHT!
84.9K33