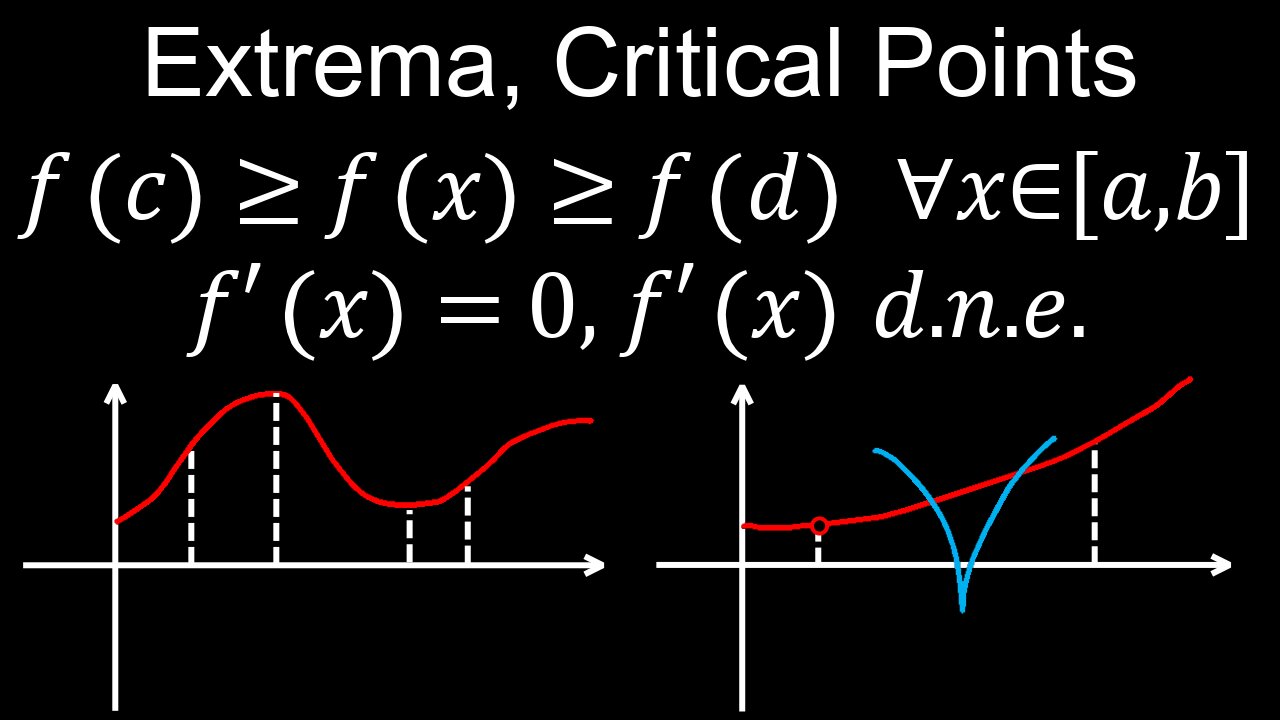
Extreme Value Theorem, Visual Proof, Critical Points, Global and Local Extrema - Calculus

This video explains the extreme value theorem for finding global (absolute) extrema and critical points (local or relative extrema) of functions on a closed interval, which are covered in basic calculus (calc 1, engineering mathematics). You will understand the meaning and why the topic is important through the conditions for extreme values in the definition and example graphs. The first and second derivative test will be covered later on, from which you will be able to distinguish critical points from inflection points. A worksheet (PDF) of problems with solutions is provided for practice.

📌 Worksheets are provided in PDF format to further improve your understanding:

- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link

📌 Chapters on What You’ll Learn:

00:00 Extreme value theorem
01:11 Critical points
02:09 Global and local extrema
03:17 Worked examples

📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.

👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!

– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.

🔴Subscribe: https://rumble.com/user/drofeng

What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng