Premium Only Content
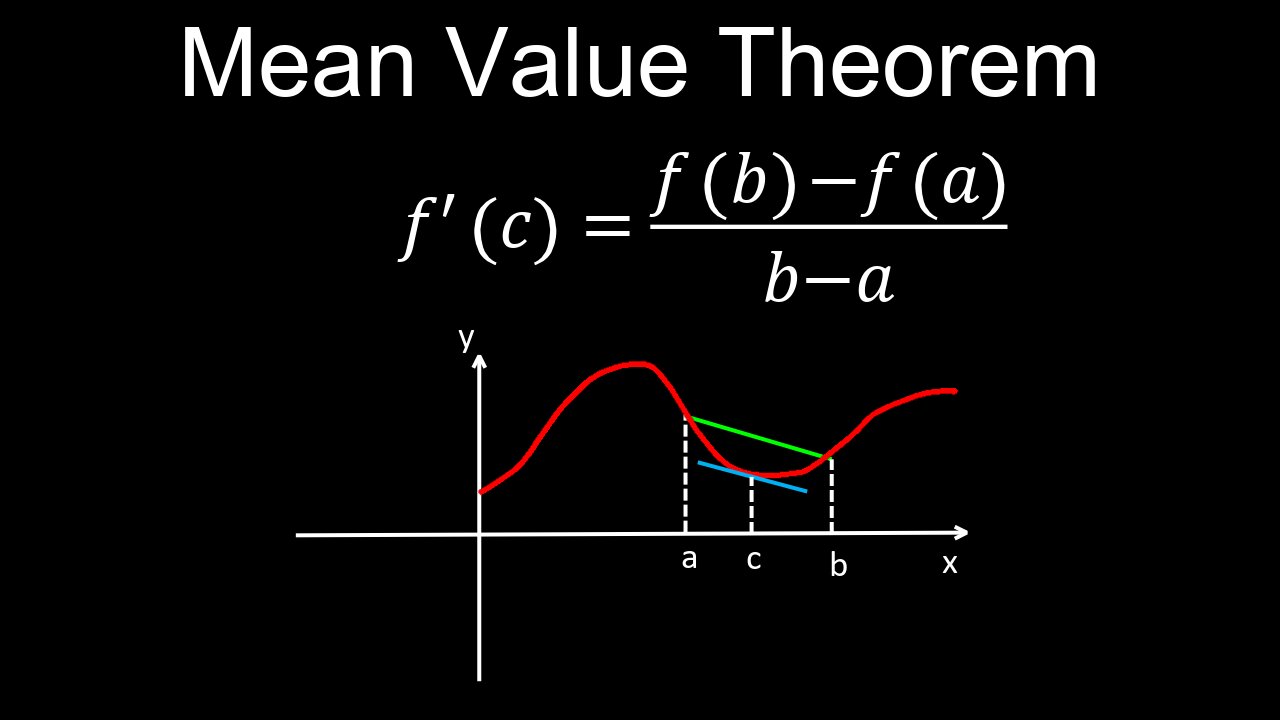
Mean Value Theorem, Derivatives, Definition, Visual Proof, Examples - Calculus
This video explains what is the mean value theorem MVT for differentiation and how it is used in calculus. The MVT formula is covered in class 12 and engineering mathematics and helps with understanding derivatives. Continuity and differentiability are the that need to be satisfied for application of the MVT to first order and higher order derivatives. A worksheet (PDF) of questions with solutions is provided for practice, which includes applications to instantaneous and average velocity and second order derivatives.
📌 Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1-6NeYDqLKVXwGn2cLGddt-RgPwE6BRkS/view?usp=drive_link
- Answers: https://drive.google.com/file/d/1ZcFgkcsWJvJAyThTUTCfGbEP0LqGLGtx/view?usp=drive_link
📌 Chapters on What You’ll Learn:
00:00 MVT definition and visual proof
01:01 Worked example
📌 Perfect for calculus students and exam preparation, this tutorial uses plenty of examples and easy-to-follow explanations.
👉 Make sure to check out our full Calculus 1 and 2 course playlist, which covers differentiation, integration, sequences and series and their applications!
– Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔴Subscribe: https://www.youtube.com/channel/UCJAvCW22EeE_2s2ZlJne7uQ?sub_confirmation=1
What part of Analytical Applications of Differentiation gave you the most difficulty? Comment below!👇
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://rumble.com/user/drofeng
-
 8:39
8:39
MetatronHistory
1 day agoWhy Did We Switch From Bronze to Iron in Classical Antiquity?
4.21K -
 11:01
11:01
MattMorseTV
13 hours ago $10.07 earnedEU caught in $140,000,000 SCANDAL.
14.2K48 -
 1:44:46
1:44:46
PandaSub2000
10 hours agoUltimate Chicken Horse | ULTRA BEST AT GAMES (HD Edited Replay)
4.66K -
 1:47:16
1:47:16
omarelattar
2 days agoTroy Eckard Shares His Rags to Riches Story
6.4K -
 26:18
26:18
GritsGG
14 hours agoHow to Activate Heat Map & Find Self Revives On Warzone!
4.79K -
 29:01
29:01
The Pascal Show
1 day ago $8.54 earnedRUNNING SCARED! Candace Owens DESTROYS TPUSA! Are They Backing Out?!
39.6K48 -
 24:45
24:45
Blabbering Collector
1 day agoUnboxing The 2025 Diagon Alley Advent Calendar By Carat Shop | Harry Potter
5.77K -
 0:43
0:43
Gaming on Rumble
1 day ago $5.65 earnedLvl UP (Raids)
38.9K2 -
 19:07
19:07
MetatronGaming
1 day agoWe need to find a way out NOW!
5.88K -
 1:11:16
1:11:16
omarelattar
4 days agoHow I Went From Depressed w/ $0 To $500 Million Per Year In My 20's (COMFRT CEO Hudson Leogrande)
6.5K