Premium Only Content
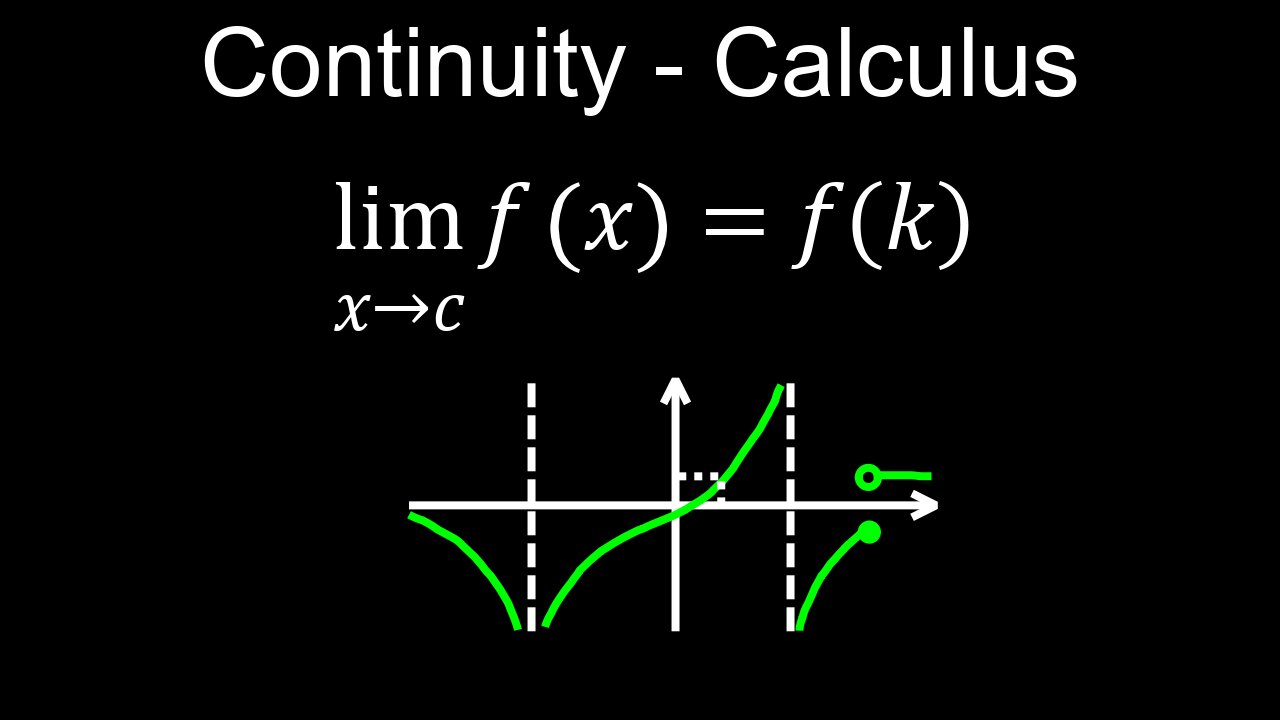
Continuity of a Function, Definition, 3 Conditions, Discontinuities, Practice Examples - Calculus
In calculus, a function is continuous if its graph can be drawn without lifting your pen, meaning there are no breaks or jumps. More formally, a function f(x) is continuous at a point a if three conditions are met: f(a) is defined, the limit of f(x) as x approaches a exists, and the limit equals f(a).
💡Intuitive Understanding
• No Gaps or Jumps: You can draw the graph of a continuous function without your pencil leaving the paper.
• Small Input, Small Output: A small change in the input (x) results in a small change in the output (f(x)).
💡The Formal Definition (at a Point a)
For a function f(x) to be continuous at a point a, all three of the following conditions must be true:
• f(a) is defined: The function must have a specific, defined value at the point a.
• The limit of f(x) as x approaches a exists: The function must approach the same value as x gets closer and closer to a from both the left and right sides.
• The limit equals the function value: The value the function approaches (the limit) must be the same as the actual value of the function at a, i.e., lim x→a f(x) = f(a).
💡Discontinuities
If any of these three conditions are not met, the function is discontinuous at that point. Common types of discontinuities include:
• Removable: A "hole" in the graph that could be "filled".
• Jump: The graph jumps from one value to another, like the function f(x) = {-1 for x less than or equal to 0 and 1 for x greater than 0 at x=0}.
• Infinite: A vertical asymptote where the function's value goes to positive or negative infinity.
💡Worksheets are provided in PDF format to further improve your understanding:
- Questions Worksheet: https://drive.google.com/file/d/1IfdCaeJTszq4Is48tDhUUxlMd-w9Eltx/view?usp=drive_link
- Answers: https://drive.google.com/file/d/11PKq7Z-aEJQOqR_xbqFdAEQdQH4JjKnu/view?usp=drive_link
💡Chapters:
00:00 Types of discontinuities
01:58 Discontinuities, examples
04:26 Continuity at a point, with examples
08:16 Continuity over an interval, with example
10:55 Removing discontinuities, with example
13:42 Infinite limits and vertical asymptotes
14:41 Infinite limits and horizontal asymptotes
15:34 Relative magnitudes of functions
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 LIVE
LIVE
Sean Unpaved
1 hour agoMNF Jaguars Shock: Is Bill's Cachet Fading? Hot Seat Sizzlers & Sanchez's Stabby Spiral
93 watching -
 1:48:42
1:48:42
Steven Crowder
3 hours agoDid You Vote for This: Why The Podcast Bros are Turning on Trump
239K246 -
 1:08:40
1:08:40
The Rubin Report
2 hours agoListen to ‘The View’ Crowd Gasp as Whoopi Tells Super Bowl Crowd to Do This
20.3K33 -
 LIVE
LIVE
LFA TV
14 hours agoLIVE & BREAKING NEWS! | TUESDAY 10/7/25
3,872 watching -
 LIVE
LIVE
Rebel News
32 minutes agoTamara Lich sentencing, Two years since Hamas attack, Carney meets Trump | Rebel Roundup
335 watching -
 LIVE
LIVE
TheAlecLaceShow
1 hour agoICE Under Siege in Chicago & Portland | Guests: Douglass Mackey & Wid Lyman | The Alec Lace Show
53 watching -
 LIVE
LIVE
The Mel K Show
1 hour agoMORNINGS WITH MEL K -Overwhelming Evidence of Grand Conspiracy Against We the People 10-7-25
780 watching -
 LIVE
LIVE
The Shannon Joy Show
12 hours agoEugenics, Vaccination & The Unholy Trump/Pfizer Alliance LIVE W/ Brook Jackson & Warner Mendenhall
259 watching -
 31:12
31:12
Grant Stinchfield
1 hour agoWhen Science Became Propaganda
3.9K4 -
 1:01:30
1:01:30
Trumpet Daily
1 hour agoTrumpet Daily LIVE | Oct. 7, 2025
5.25K1
