Premium Only Content
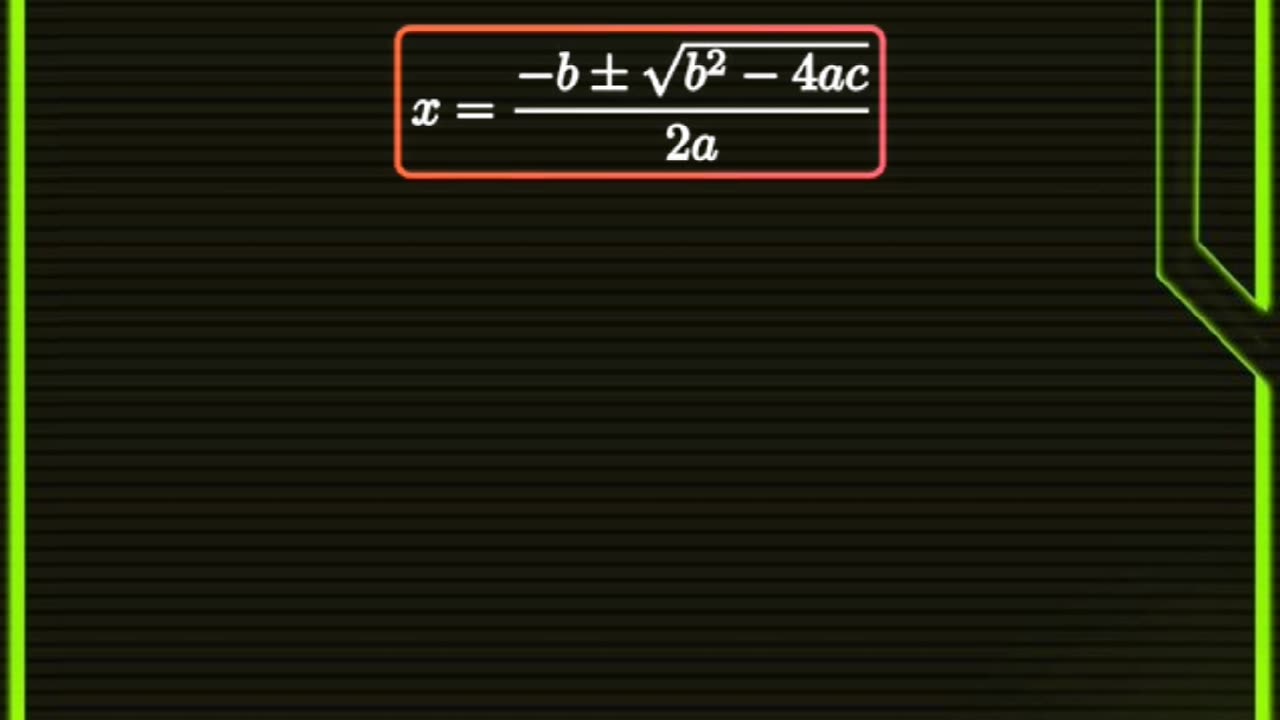
How to derive quadratic formula
Quadratic formula
The quadratic formula is a powerful tool for solving any quadratic equation. It is a formula used to find the roots (or solutions) of a quadratic equation in its standard form. A quadratic equation is a second-degree polynomial equation.
The Formula
The standard form of a quadratic equation is:
ax^2 + bx + c = 0
where a, b, and c are coefficients, with a not equal to 0.
The quadratic formula is:
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
To use it, you just need to identify the values of a, b, and c from your equation and plug them into the formula to solve for x. The "\pm" symbol means there are two possible solutions: one where you add the square root and one where you subtract it.
Key Components
* Discriminant: The expression under the square root, b^2 - 4ac, is called the discriminant. It tells you about the nature of the solutions without solving the entire equation.
* If b^2 - 4ac > 0, there are two distinct real solutions.
* If b^2 - 4ac = 0, there is exactly one real solution.
* If b^2 - 4ac < 0, there are two complex (non-real) solutions.
Common Applications
Quadratic equations and the quadratic formula are used in many real-world applications, especially in physics and engineering, to model situations that involve a parabolic path. Some examples include:
* Projectile Motion: Calculating the trajectory of a thrown ball, a launched rocket, or a bouncing object.
* Area and Geometry: Solving problems involving the area of a shape where the dimensions are related to a single variable.
* Business: Determining the maximum profit or minimum cost for a product.
* Engineering: Designing structures like suspension bridges and satellite dishes, which often use parabolic shapes.
-
 LIVE
LIVE
Dr Disrespect
1 hour ago🔴LIVE - DR DISRESPECT - CRONOS: The New Dawn - FIRST IMPRESSIONS
513 watching -
 LIVE
LIVE
Steven Crowder
2 hours ago🔴 India First! MAGA Influencers Caught Pushing Insanely Stupid Propaganda
20,717 watching -
 1:00:39
1:00:39
The Rubin Report
1 hour agoIt’s Official: Border Czar Names the Four Blue Cities Trump Will Target Next
5.58K3 -
 LIVE
LIVE
The Mel K Show
58 minutes agoMORNINGS WITH MEL K - Clown Show in DC RFK Jr. Hearing Prove We the People are the Only Answer 9-5-25
517 watching -
 LIVE
LIVE
Film Threat
17 hours agoTHE CONJURING: LAST RITES + SPLITSVILLE + TONS OF REVIEWS! | Film Threat Livecast
57 watching -
 59:45
59:45
VINCE
3 hours agoRFKage Match! Kennedy Destroys Corrupt Senators In Wild Hearing | Episode 119 - 09/05/25
127K90 -
 LIVE
LIVE
LFA TV
5 hours agoLFA TV ALL DAY STREAM - FRIDAY 9/5/25
3,264 watching -
 LIVE
LIVE
Benny Johnson
2 hours agoBiden Appears With MASSIVE Scar on Face, New Health Horror Revealed! Sobbing Jimmy Kimmel FLEEING US
4,407 watching -
 LIVE
LIVE
The Big Mig™
4 hours agoBig Pharma's Puppets: RFK Jr. Takes on Congress
8,302 watching -
 LIVE
LIVE
Total Horse Channel
12 hours ago2025 Reno Snaffle Bit Futurity | Friday
24 watching