Premium Only Content
What are Set Operations?
In mathematics, a set is a collection of distinct objects or elements. Set operations are ways of combining or manipulating these sets to create new ones. Think of them like basic arithmetic operations (addition, subtraction, etc.) but for sets instead of numbers. These operations are fundamental to fields like computer science, logic, and probability.
The most common set operations are union, intersection, and difference. They are often visualized using Venn diagrams, which show the relationships between different sets with overlapping circles.
Here's a breakdown of the main operations:
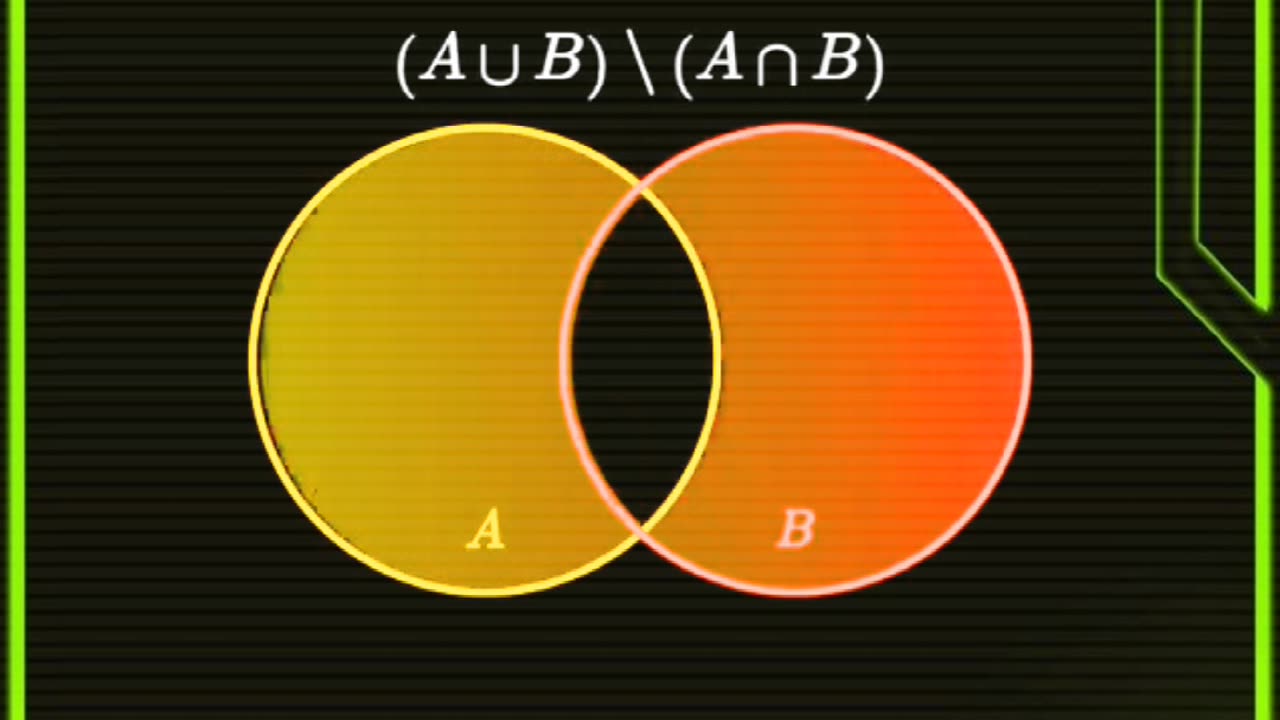
1. Union (A \cup B)
The union of two sets, A and B, is a new set that contains all the elements from both A and B, without any duplicates.
* Description: It combines the two sets into one larger set.
* Example: If set A = \{1, 2, 3\} and set B = \{3, 4, 5\}, then the union A \cup B = \{1, 2, 3, 4, 5\}. Notice that the number 3 is only listed once.
2. Intersection (A \cap B)
The intersection of two sets, A and B, is a new set that contains only the elements that are common to both A and B.
* Description: It finds the "overlap" between the two sets.
* Example: If set A = \{1, 2, 3\} and set B = \{3, 4, 5\}, then the intersection A \cap B = \{3\}.
3. Difference (A - B or A \setminus B)
The difference of two sets, A and B, is a new set containing all the elements that are in set A but are not in set B.
* Description: It removes the elements of B from A. The order matters here: A - B is not the same as B - A.
* Example: If set A = \{1, 2, 3\} and set B = \{3, 4, 5\}, then the difference A - B = \{1, 2\}.
* In contrast, B - A = \{4, 5\}.
4. Complement (A^c or A')
The complement of a set A is a new set that contains all the elements that are not in A, but are within a defined universal set (U).
* Description: It's everything outside of A, but still within the larger context or "universe" you're working in.
* Example: If the universal set U = \{1, 2, 3, 4, 5\} and set A = \{1, 2\}, then the complement A^c = \{3, 4, 5\}.
-
 1:04:36
1:04:36
Dialogue works
2 days ago $0.21 earnedMohammad Marandi: Iran Just Gave Israel a FINAL Warning…
2.45K4 -
 9:20
9:20
daniellesmithab
1 day ago3 Bad Laws
11.2K5 -
 9:22
9:22
MattMorseTV
16 hours ago $9.09 earnedINDIA just made a BIG MISTAKE.
53.1K51 -
 12:11
12:11
Nikko Ortiz
14 hours agoCrashout 6 Rumble
8.61K2 -
 22:35
22:35
GritsGG
14 hours agoThe KILO is BACK! The Best AR on Warzone FRIES!
16.2K1 -
 2:16:36
2:16:36
Side Scrollers Podcast
18 hours agoStreamer KICKED OUT of Renaissance Fair for Misgendering + Spiderman MELTDOWN | Side Scrollers Live
39.8K7 -
 12:29
12:29
The Pascal Show
1 day ago $1.14 earnedLOCKED IN A DUNGEON?! Parents Arrested After 5 Children Found In 'Dungeon' At Home
9.96K3 -
 LIVE
LIVE
Lofi Girl
2 years agoSynthwave Radio 🌌 - beats to chill/game to
226 watching -
 3:07:24
3:07:24
FreshandFit
10 hours agoPrivileged Nigerian Thinks Women Created Everything: HEATED DEBATE
146K80 -
 5:57:27
5:57:27
SpartakusLIVE
10 hours agoNEW Update - BROKEN Attachment || Viewers REJOICE at the long-awaited Return of Their KING
77.9K