Premium Only Content
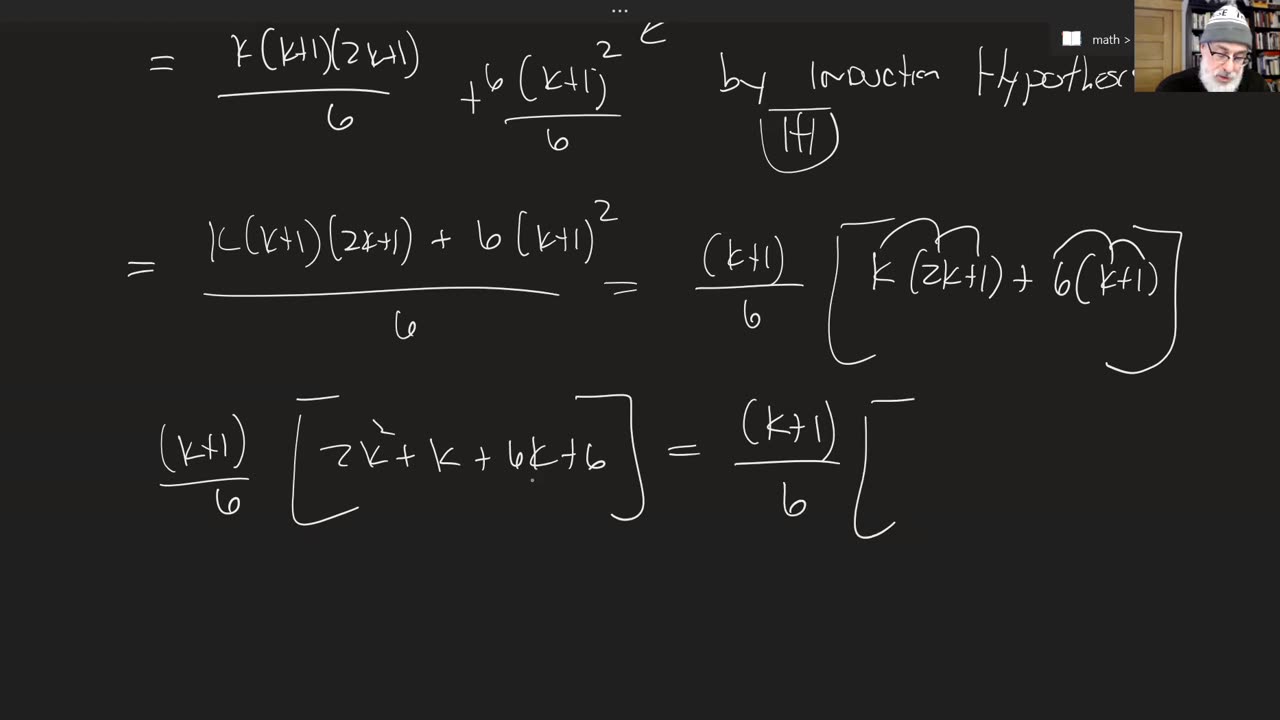
Discrete Math. Prove that the sum of squares of the first n positive integers = (n(n+1)(n+2))/6
In this video, we prove by induction that the sum of square of the first n positive integers is equal to (n(n+1)(n+2))/6. This problem was taken from Discrete Mathematics and Its Applications by Kenneth Rosen, 7th edition, Chapter 5.1, question 3.
1^2 + 2^2 + 3^2 + ... + n^2 = (n(n+1)(n+2))/6
Discrete Mathematics playlist:
https://youtube.com/playlist?list=PLm90IN9RVLf_BneWC40564ZZAqpe2sz6-&si=bKhYao84EXCHpl6N
Induction Proofs playlist:
https://youtube.com/playlist?list=PLm90IN9RVLf-z-V3NIPi0-ZhxckZHup9q&si=hIv_gDttX16fM1F5
Chapters:
00:00 Introduction to Question
01:13 Base Case P(1)
02:58 Inductive Step
03:20 Induction Hypothesis P(k)
04:51 We Want to Show P(k+1) Case
06:53 Algebra Steps
12:23 QED Thanks for Watching
#discrete_mathematics #discretemathematics #induction_proof #induction #integers #integerproof #sumofcubes
-
 LIVE
LIVE
LFA TV
2 hours agoLFA TV ALL DAY STREAM - THURSDAY 9/4/25
8,051 watching -
 1:16:35
1:16:35
JULIE GREEN MINISTRIES
2 hours agoLIVE WITH JULIE
29.9K88 -
 LIVE
LIVE
Welcome to the Rebellion Podcast
12 hours agoDon3po is Live - WTTR Podcast Live 9/4
198 watching -
 13:43
13:43
The Kevin Trudeau Show Limitless
23 hours agoClassified File 3 | Kevin Trudeau EXPOSES Secret Society Brainwave Training
44.5K9 -
 LIVE
LIVE
The Chris Salcedo Show
13 hours agoAmericans Are Tired Of Leftists & Fake-GOP Who Cater To Them
542 watching -
 1:12:23
1:12:23
Game On!
20 hours ago $0.94 earnedFootball IS BACK! Cowboys vs Eagles Opening Night Kickoff!
7.32K1 -
 LIVE
LIVE
The Bubba Army
23 hours ago#1 Documentary IN THE WORLD! - Bubba the Love Sponge® Show | 9/04/25
1,660 watching -
 39:31
39:31
Her Patriot Voice
14 hours ago $1.84 earnedBlack Conservative Surrounded + ROBBED By Leftists!
11.2K25 -
 13:25
13:25
The Gun Collective
14 hours agoWOW! A LOT of new GUNS just dropped!
12.7K8 -
 2:02:53
2:02:53
BEK TV
1 day agoTrent Loos in the Morning - 9/04/2025
9.47K