Premium Only Content
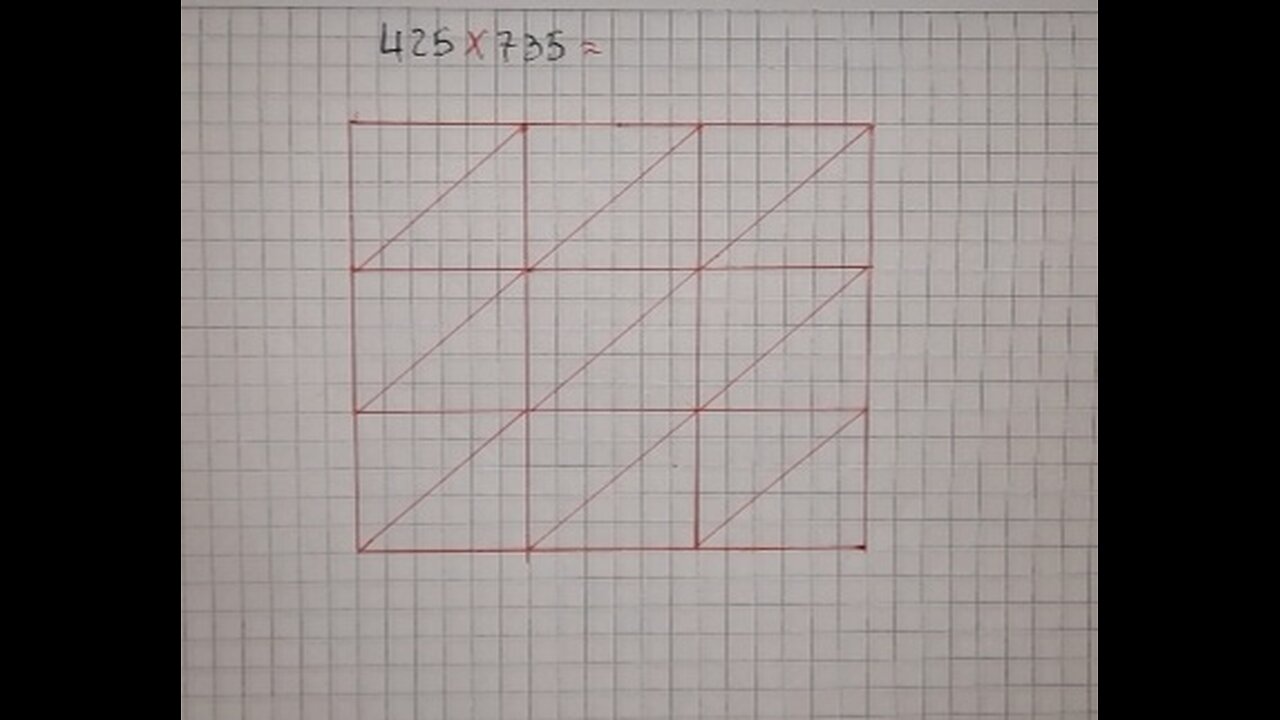
The hindu method of multiplication : application exercise
The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".
Features of the method
1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.
Method steps
1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in the form of positional numbering.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.
Example
Multiply 432 by 27:
1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the
[11/1 8:00 a.m. m.] Meta AI: The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".
Features of the method
1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.
Method steps
1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in the form of positional numbering.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.
Example
Multiply 432 by 27:
1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the result to the next column: 108 → 100 + 8.
8. Add the results: 100 + 80 + 50 + 8 + 4 + 1 = 11664.
The final product is 11664.
Advantages of the method
1. _Easy to understand_: The method is easy to understand and apply
[11/1 8:00 a.m. m.] Meta AI: The Hindu method of multiplication is a multiplication algorithm that originated in India at the time of the Gupta Empire (320-550 AD). This method is also known as "place multiplication method" or "Hindu multiplication method".
Features of the method
1. _Use of positional numbering_: The method uses positional numbering, that is, each digit has a specific place in the numerical representation.
2. _Multiplication by place_: The method involves multiplying each digit of the multiplicand by the multiplier, starting from the rightmost place.
3. _Use of the "gate"_: The method uses a "gate" to carry the results of the multiplication to the next column.
Method steps
1. _Write the multiplicand and the multiplier_: Write the multiplicand and the multiplier in positional numbering form.
2. _Multiply the rightmost digit of the multiplicand by the multiplier_: Multiply the rightmost digit of the multiplicand by the multiplier and write the result in the corresponding column.
3. _Take the result to the next column_: Take the result of the multiplication to the next column, using the "door" to do so.
4. _Repeat steps 2 and 3_: Repeat steps 2 and 3 for each digit of the multiplicand.
5. _Add the results_: Add the results of each multiplication to obtain the final product.
Example
Multiply 432 by 27:
1. Write the multiplicand and the multiplier: 432 and 27.
2. Multiply the rightmost digit of the multiplicand by the multiplier: 2 × 27 = 54.
3. Take the result to the next column: 54 → 50 + 4.
4. Multiply the next digit of the multiplicand by the multiplier: 3 × 27 = 81.
5. Take the result to the next column: 81 → 80 + 1.
6. Multiply the last digit of the multiplicand by the multiplier: 4 × 27 = 108.
7. Take the result to the next column: 108 → 100 + 8.
8. Add the results: 100 + 80 + 50 + 8 + 4 + 1 = 11664.
The final product is 11664.
Advantages of the method
1. _Easy to understand_: The method is easy to understand and apply.
2. _Fast_: The method is fast and efficient for multiplying large numbers.
3. _Flexible_: The method can be applied to numbers of any size.
Disadvantages of the method
1. _Requires practice_: The method requires practice to master.
2. _Can be confusing_: The method can be confusing if positional numbering is not well understood.
In short, the Hindu method of multiplication is an efficient and easy-to-understand algorithm used to multiply large numbers. Although it takes practice and can be confusing at first, it is a valuable tool for arithmetic and mathematics in general.
-
 UPCOMING
UPCOMING
Grant Stinchfield
17 hours agoABC SETUP: Michael McCaul Falls for Martha Raddatz Trap on Live TV!
920 -
 LIVE
LIVE
Nikko Ortiz
1 hour agoWorst Military Events And War Crimes... | Rumble LIVE
264 watching -
 17:27
17:27
We Got Receipts
2 hours agoAntifa Getting Arrested In The Funniest Ways!
5.28K6 -
 LIVE
LIVE
Caleb Hammer
10 hours agoHe Treats His Wife Like A Dog | Financial Audit
229 watching -
 LIVE
LIVE
Badlands Media
5 hours agoBadlands Daily Nov. 24, 2025
3,626 watching -
 2:12:17
2:12:17
Matt Kohrs
13 hours agoStock Market Open, Breaking News & The Week Ahead || Live Trading $1M
20.7K1 -
 LIVE
LIVE
Wendy Bell Radio
7 hours agoWhy Do Democrats Put America Last?
6,852 watching -
 1:36:29
1:36:29
Graham Allen
3 hours agoIs The MAGA Divorce Real Or Did Elon Just Expose It’s FAKE?!
125K597 -
 LIVE
LIVE
The Big Mig™
4 hours agoTrump, We Must Focus All Our Energy & Might On Election Fraud
3,395 watching -
 15:51
15:51
Demons Row
12 hours ago $1.35 earnedOutlaw Motorcycle Clubs You Were NEVER Supposed to Know About 💀🏍️
18.1K4