Premium Only Content
Droz-Farny line theorem | plane geometry | advanced level
Episode 122.
Droz-Farny line theorem | plane geometry | advanced level.
Branch of mathematics: plane geometry.
Difficulty level: advanced.
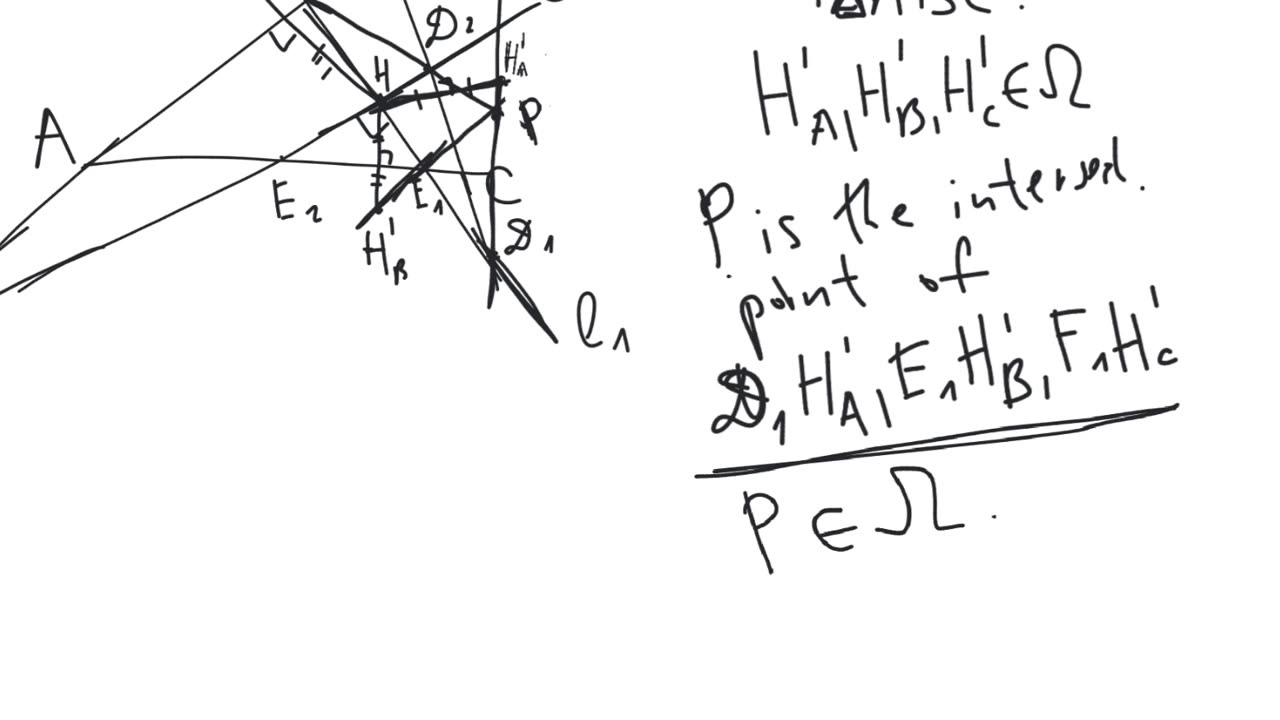
Droz-Farny line theorem. Let $ABC$ be a triangle with orthocenter $H$. Let $\ell_1$ and $\ell_2$ be two perpendicular lines passing through $H$. Let $D_1$, $E_1$, $F_1$ be the intersection points of $\ell_1$ and the lines $BC$, $CA$, $AB$ respectively. Let $D_2$, $E_2$, $F_2$ be the intersection points of $\ell_2$ and the lines $BC$, $CA$, $AB$ respectively. Then the midpoints of the segments $D_1D_2$, $E_1E_2$, $F_1F_2$ are collinear.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/Wgd2WKy_Dfk
The same video on Telegram:
https://t.me/mathematical_bunker/147
-
 LIVE
LIVE
Midnight In The Mountains™
3 hours agoThe Midnights Play Arc Raiders | Loot Scoot and KILL | Crypto Wallet up n running GO JOIN THE BETA!
122 watching -
 53:25
53:25
X22 Report
5 hours agoMr & Mrs X - Trump Is Using The Same Tactic As Our Founding Fathers To Rebuild America - EP 17
77.8K17 -
 LIVE
LIVE
PudgeTV
2 hours ago🟣 Arc Raiders - Gaming on Rumble | Going Topside w My Daughter’s Husband
82 watching -
 2:05:43
2:05:43
LFA TV
21 hours agoRUMBLE RUNDOWN WEEK 7 with SHAWN FARASH 11.22.25 9AM
139K7 -
 LIVE
LIVE
ttvglamourx
2 hours ago $1.14 earnedGLAMOURX VS CALL OF DUTY LOBBIES !DISCORD
128 watching -
 LIVE
LIVE
DannyStreams
4 hours agoSaturday Morning Tarky
57 watching -
 1:12:53
1:12:53
Wendy Bell Radio
8 hours agoPet Talk With The Pet Doc
30.5K20 -
 LIVE
LIVE
CHiLi XDD
2 hours agoFF7 Remake | Materia Hunting at its finest!
61 watching -
 33:49
33:49
SouthernbelleReacts
21 hours ago $1.63 earnedNOT THE GOPHER 😭🤣 | First Time Watching Caddyshack
16K3 -
 26:19
26:19
marcushouse
5 hours ago $6.50 earnedStarship Super Heavy Just Blew Itself Apart! 🤯 What Happened Here!?
19.3K10