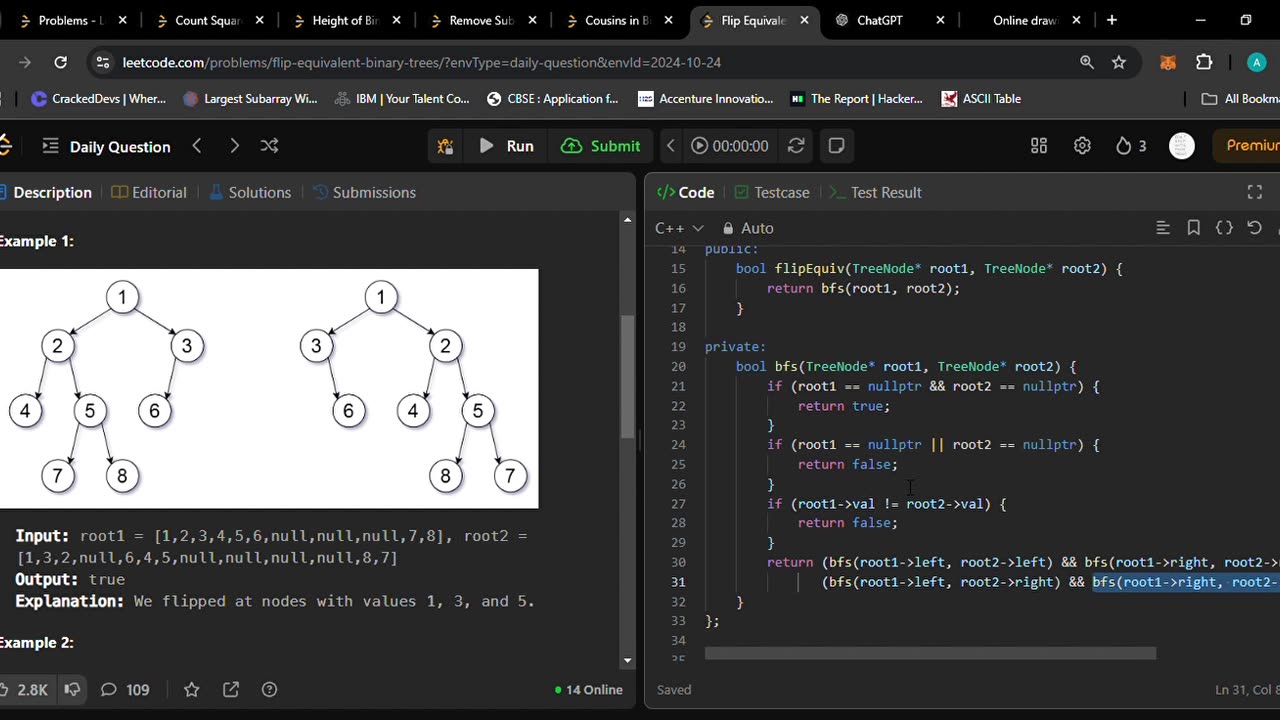
951. Flip Equivalent Binary Trees

Code:-
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/

class Solution {
public:
bool flipEquiv(TreeNode* root1, TreeNode* root2) {
return bfs(root1, root2);
}

private:
bool bfs(TreeNode* root1, TreeNode* root2) {
if (root1 == nullptr && root2 == nullptr) {
return true;
}
if (root1 == nullptr || root2 == nullptr) {
return false;
}
if (root1->val != root2->val) {
return false;
}
return (bfs(root1->left, root2->left) && bfs(root1->right, root2->right)) ||
(bfs(root1->left, root2->right) && bfs(root1->right, root2->left));
}
};

Question:-
For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.

A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.

Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.

Example 1:

Flipped Trees Diagram
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.
Example 2:

Input: root1 = [], root2 = []
Output: true
Example 3:

Input: root1 = [], root2 = [1]
Output: false

Constraints:

The number of nodes in each tree is in the range [0, 100].
Each tree will have unique node values in the range [0, 99].