Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.
The second Fermat-Torricelli point of a triangle | plane geometry | intermediate level
23 days ago
17
Science
mathematics
geometry
plane geometry
classical geometry
Euclidean geometry
triangle
line
Fermat
Torricelli
second Fermat-Torricelli point
Episode 112.
The second Fermat-Torricelli point of a triangle | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
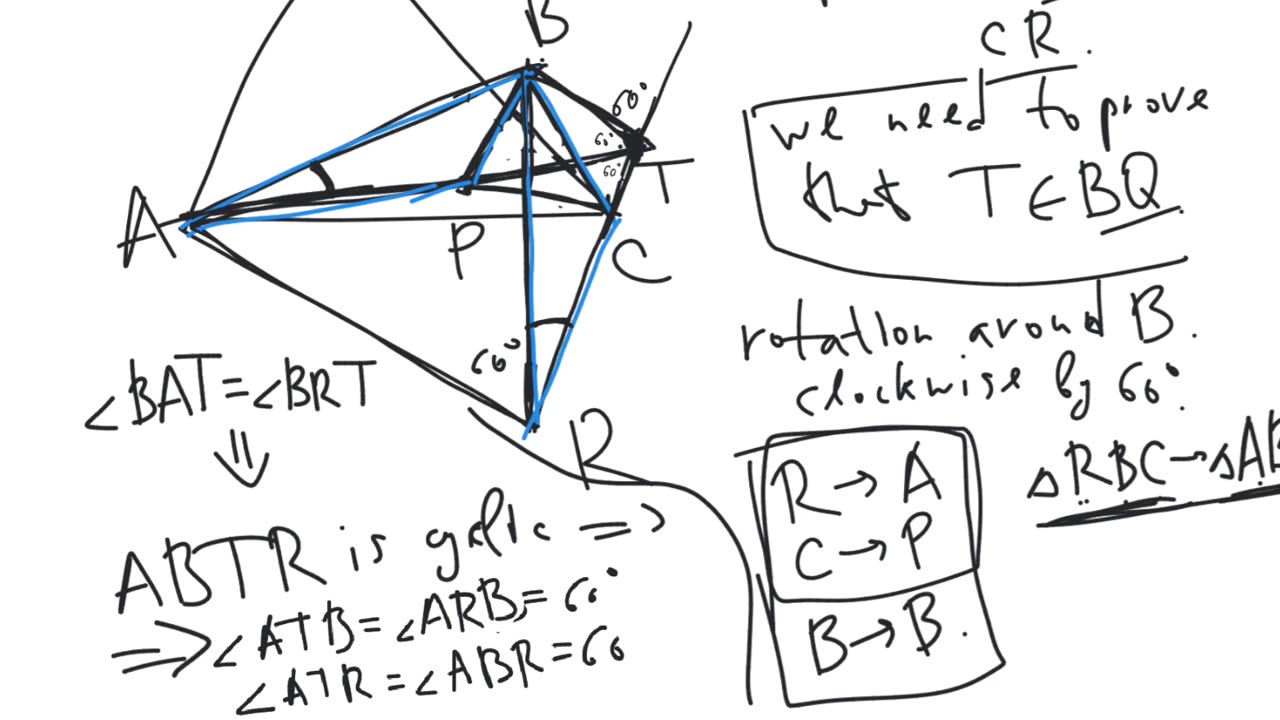
Theorem. Let $ABC$ be a triangle. Let $BCP$, $CAQ$, $ABR$ be equilateral triangles constructed on the sides of the triangle $ABC$ to the inside. Then the lines $AP$, $BQ$, $CR$ intersect at a single point, which is called the second Fermat-Torricelli point of the triangle $ABC$.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/DJHU1Kob1Hw
The same video on Telegram:
https://t.me/mathematical_bunker/137
Loading comments...
-
 47:13
47:13
PMG
17 hours ago"Hannah Faulkner and Doug Billings | WHY LIBERALS LOST THE ELECTION"
252 -
 59:01
59:01
The Liberty Lobbyist
3 hours ago"We Only Have NOW To Make a Difference"
1401 -
 4:16:41
4:16:41
CatboyKami
4 hours agoStalker 2 Blind playthrough pt1
551 -
 1:06:27
1:06:27
Russell Brand
5 hours agoNeil Oliver on the Rise of Independent Media, Cultural Awakening & Fighting Centralized Power –SF498
171K228 -
 1:39:14
1:39:14
vivafrei
5 hours agoSoros Karma in New York! Tammy Duckwarth Spreads LIES About Tulsi Gabbard! Pennsylvania FLIPS & MORE
63.2K60 -
 1:57:36
1:57:36
The Charlie Kirk Show
4 hours agoInside the Transition + The Bathroom Battle + Ban Pharma Ads? | Rep. Mace, Tucker, Carr | 11.21.24
129K49 -
 59:20
59:20
The Dan Bongino Show
7 hours agoBitter CNN Goes After Me (Ep. 2375) - 11/21/2024
850K3.33K -
 57:28
57:28
TheMonicaCrowleyPodcast
2 hours agoThe Monica Crowley Podcast: Mandate into Action
3.19K -
 1:02:09
1:02:09
TheAlecLaceShow
5 hours agoGuests: Alex Marlow & Terry Schilling | Justice For Laken Riley | Russian ICBM | The Alec Lace Show
31K8 -
 1:51:15
1:51:15
Danny Haiphong
4 hours ago $8.91 earnedMARK SLEBODA & SCOTT RITTER: NATO ATTACKS RUSSIA, PUTIN FIRES ICBM WARNING SHOT AT UKRAINE—WW3 NEXT?
74.9K11