Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.
The second Fermat-Torricelli point of a triangle | plane geometry | intermediate level
1 year ago
22
Health & Science
mathematics
geometry
plane geometry
classical geometry
Euclidean geometry
triangle
line
Fermat
Torricelli
second Fermat-Torricelli point
Episode 112.
The second Fermat-Torricelli point of a triangle | plane geometry | intermediate level.
Branch of mathematics: plane geometry.
Difficulty level: intermediate.
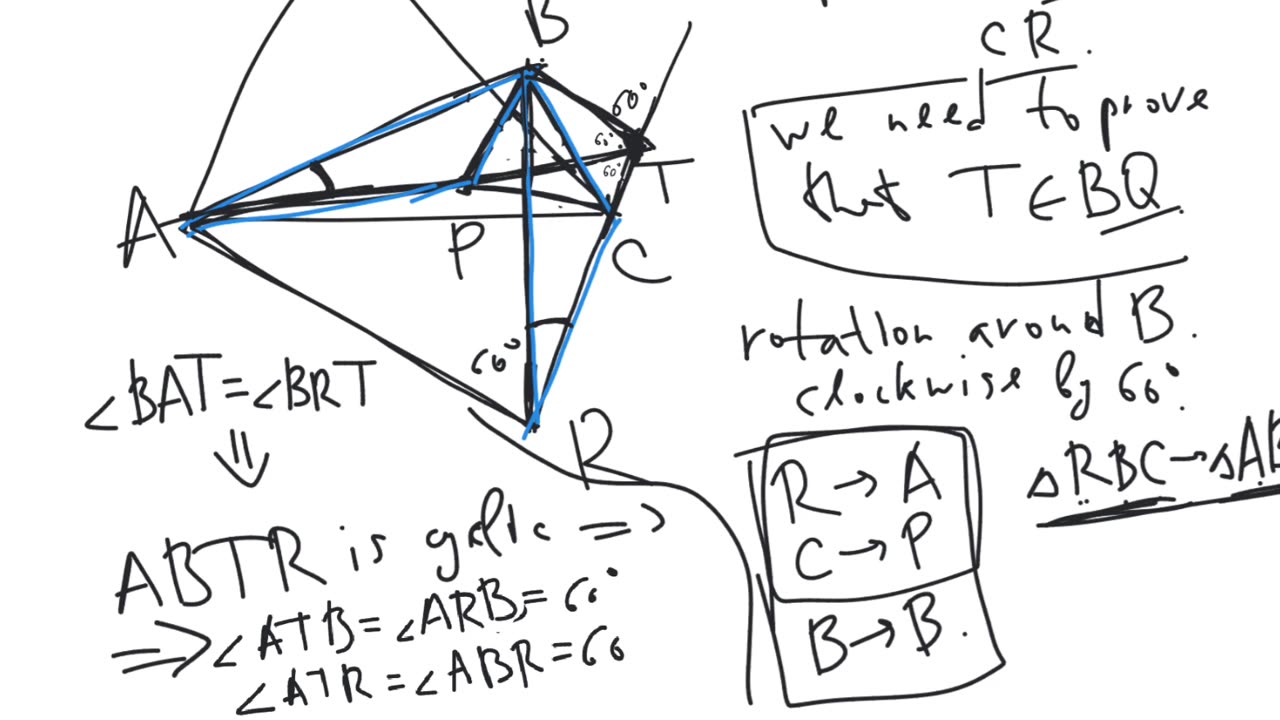
Theorem. Let $ABC$ be a triangle. Let $BCP$, $CAQ$, $ABR$ be equilateral triangles constructed on the sides of the triangle $ABC$ to the inside. Then the lines $AP$, $BQ$, $CR$ intersect at a single point, which is called the second Fermat-Torricelli point of the triangle $ABC$.
Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry
The same video on YouTube:
https://youtu.be/DJHU1Kob1Hw
The same video on Telegram:
https://t.me/mathematical_bunker/137
Loading comments...
-
 LIVE
LIVE
The Big Mig™
5 hours agoThe Big Mig Show's Greatest Hits w/ Americas Future, Karmageddon, Operation Gideon,..
185 watching -
 1:32:33
1:32:33
VapinGamers
4 hours ago $5.21 earnedTools of the Trade - EP12 The Art of Story Telling with MidnightinTheMountains - !rumbot !music
23.6K2 -
 3:09:50
3:09:50
SOLTEKGG
3 hours ago🔴LIVE - Battlefield 6 - Going Pro in RED SEC
16.1K1 -
 LIVE
LIVE
Midnight In The Mountains™
5 hours agoThe Midnights Play Arc Raiders | Loot Scoot and KILL | Crypto Wallet up n running GO JOIN THE BETA!
97 watching -
 53:25
53:25
X22 Report
6 hours agoMr & Mrs X - Trump Is Using The Same Tactic As Our Founding Fathers To Rebuild America - EP 17
89K28 -
 3:15:31
3:15:31
PudgeTV
3 hours ago🟣 Arc Raiders - Gaming on Rumble | Going Topside w My Daughter’s Husband
14K1 -
 2:05:43
2:05:43
LFA TV
23 hours agoRUMBLE RUNDOWN WEEK 7 with SHAWN FARASH 11.22.25 9AM
148K9 -
 3:23:01
3:23:01
ttvglamourx
4 hours ago $1.15 earnedGLAMOURX VS CALL OF DUTY LOBBIES !DISCORD
18.4K3 -
 LIVE
LIVE
DannyStreams
6 hours agoSaturday Morning Tarky
48 watching -
 1:12:53
1:12:53
Wendy Bell Radio
9 hours agoPet Talk With The Pet Doc
33.3K22