Premium Only Content
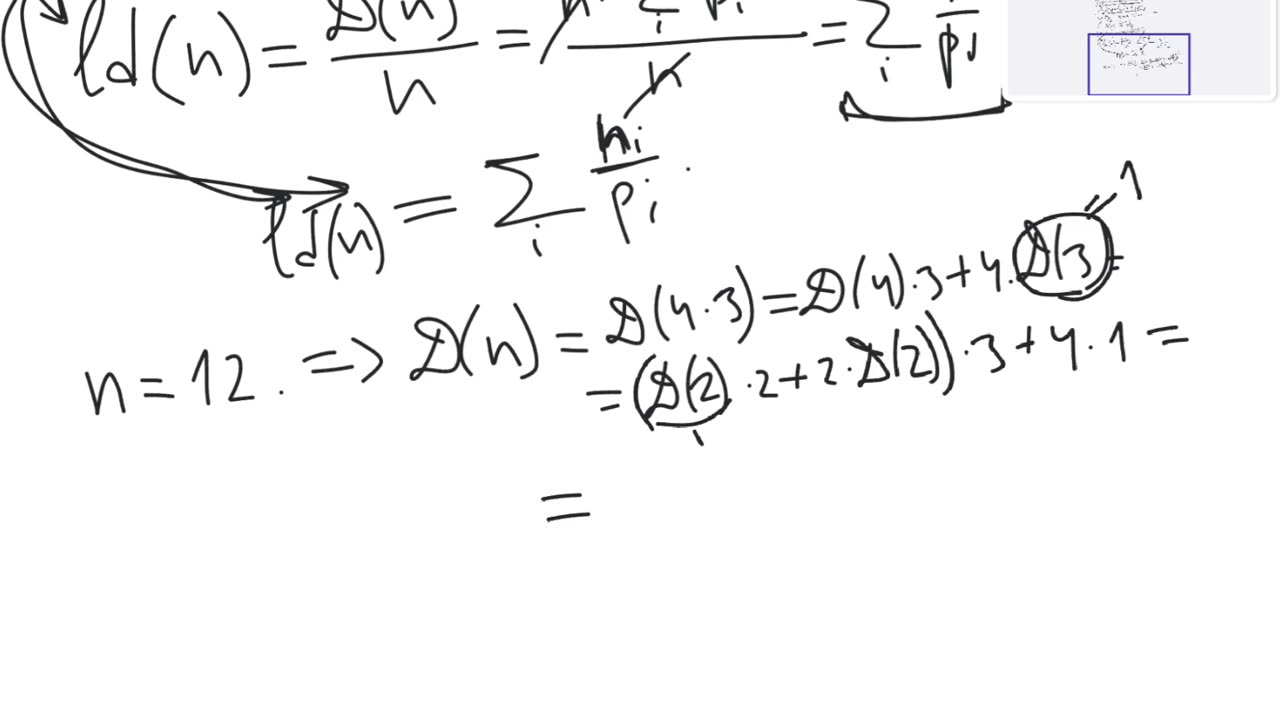
Arithmetic logarithmic derivative | number theory | advanced level
Episode 108.
Arithmetic logarithmic derivative | number theory | advanced level.
Branch of mathematics: number theory.
Difficulty level: advanced.
The arithmetic derivative is a function $D$ from natural numbers to natural numbers defined by the 2 properties:
1. For any prime number $p$, we have $D(p)=1$.
2. For any 2 natural numbers $m$ and $n$, we have $D(m \cdot n) = D(m) \cdot n + m \cdot D(n)$.
The arithmetic logarithmic derivative is defined as $ld(n) = \frac{D(n)}{n}$.
Theorem. For any 2 natural numbers $m$ and $n$, we have $ld(m \cdot n) = ld(m) + ld(n)$.
Theorem. If $n=\prod_{i}{p_i}$ is the expression of $n$ into the product of prime numbers (not necessarily distinct), then $ld(n) = \sum_{i}{\frac{1}{p_i}}$.
Mathematics. Number theory.
#Mathematics #NumberTheory
The same video on YouTube:
https://youtu.be/3jPy41jM7qw
The same video on Telegram:
https://t.me/mathematical_bunker/133
-
 31:07
31:07
Camhigby
3 days agoLeftist Claims Gender Goes By Identity, Then FLOUNDERS When Asked This Question!
132K62 -
 LIVE
LIVE
Shield_PR_Gaming
2 hours ago11/22/25 I Let's Level up on Battlefield and other games as well!
629 watching -
 10:21
10:21
MetatronGaming
8 hours agoI spent $200 for this Premium PS5 Controller. Is it worth it?
3.41K5 -
 13:46
13:46
Nikko Ortiz
16 hours agoYour Humor Might Be Broken...
34K4 -
 9:26
9:26
MattMorseTV
1 day ago $32.94 earnedPam Bondi is in HOT WATER.
48K183 -
 16:38
16:38
MetatronGaming
14 hours agoAnno 117 Pax Romana looks INCREDIBLE
76.5K8 -
 LIVE
LIVE
DillyDillerson
3 hours agoCAN'T SLEEP | Solo Raids | Trying to level up my workshop | Tips and help are welcome!
110 watching -
 LIVE
LIVE
DynastyXL
3 hours ago🔴 LIVE NOW – ARC RAIDING - BADLY! - NEW RUMBLE WALLET - THOUGHTS?
100 watching -
 2:20:13
2:20:13
Side Scrollers Podcast
21 hours agoVoice Actor VIRTUE SIGNAL at Award Show + Craig’s HORRIBLE Take + More | Side Scrollers
62.2K20 -
 LIVE
LIVE
EXPBLESS
1 hour agoShowcasing New Game | (Where Winds Meet) #RumblePremium
37 watching