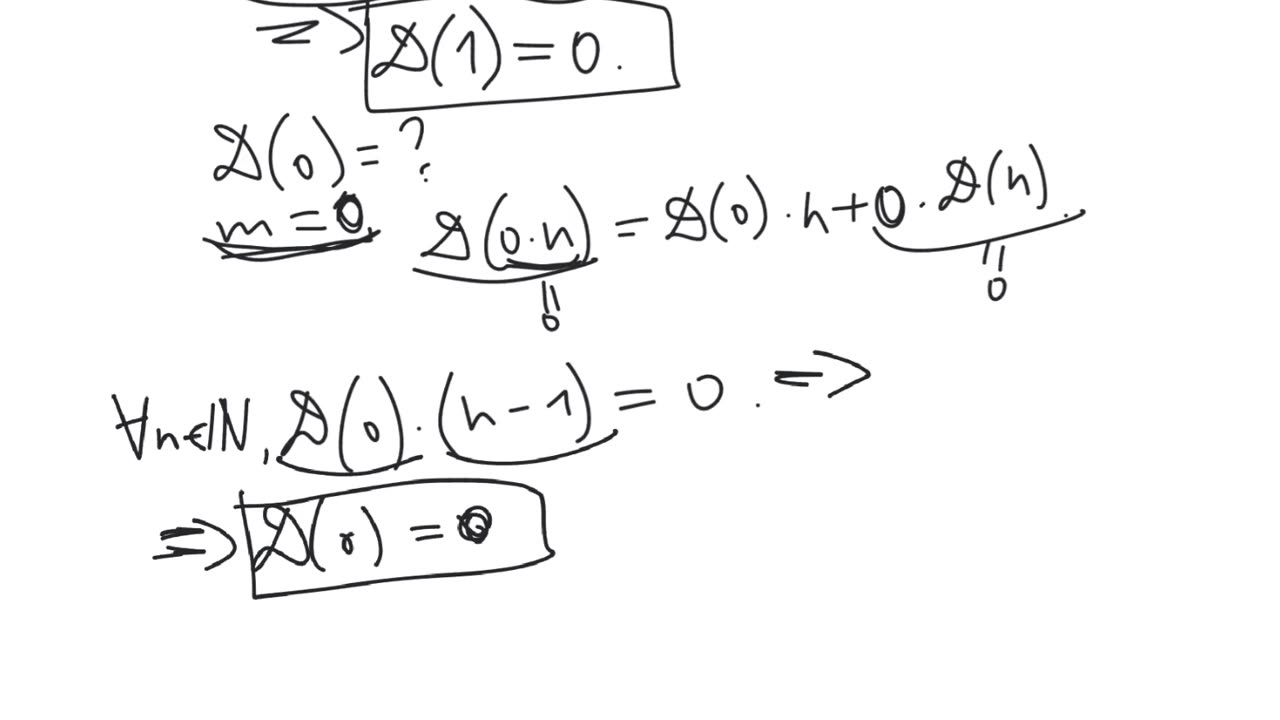
Extending the arithmetic derivative to negative numbers | number theory | advanced level

Episode 105.

Extending the arithmetic derivative to negative numbers | number theory | advanced level.

Branch of mathematics: number theory.
Difficulty level: advanced.

The arithmetic derivative is a function $D$ from natural numbers to natural numbers defined by the 2 properties:
1. For any prime number $p$, we have $D(p)=1$.
2. For any 2 natural numbers $m$ and $n$, we have $D(m \cdot n) = D(m) \cdot n + m \cdot D(n)$.

It can be proved that $D(1)=0$.

It can be extended to all integer numbers (to negative numbers and zero) like this: $D(0)=0$ and $D(-n)=-D(n)$ for any natural number $n$.

Mathematics. Number theory.
#Mathematics #NumberTheory

The same video on YouTube:
https://youtu.be/RDZzw4XnnY4

The same video on Telegram:
https://t.me/mathematical_bunker/130