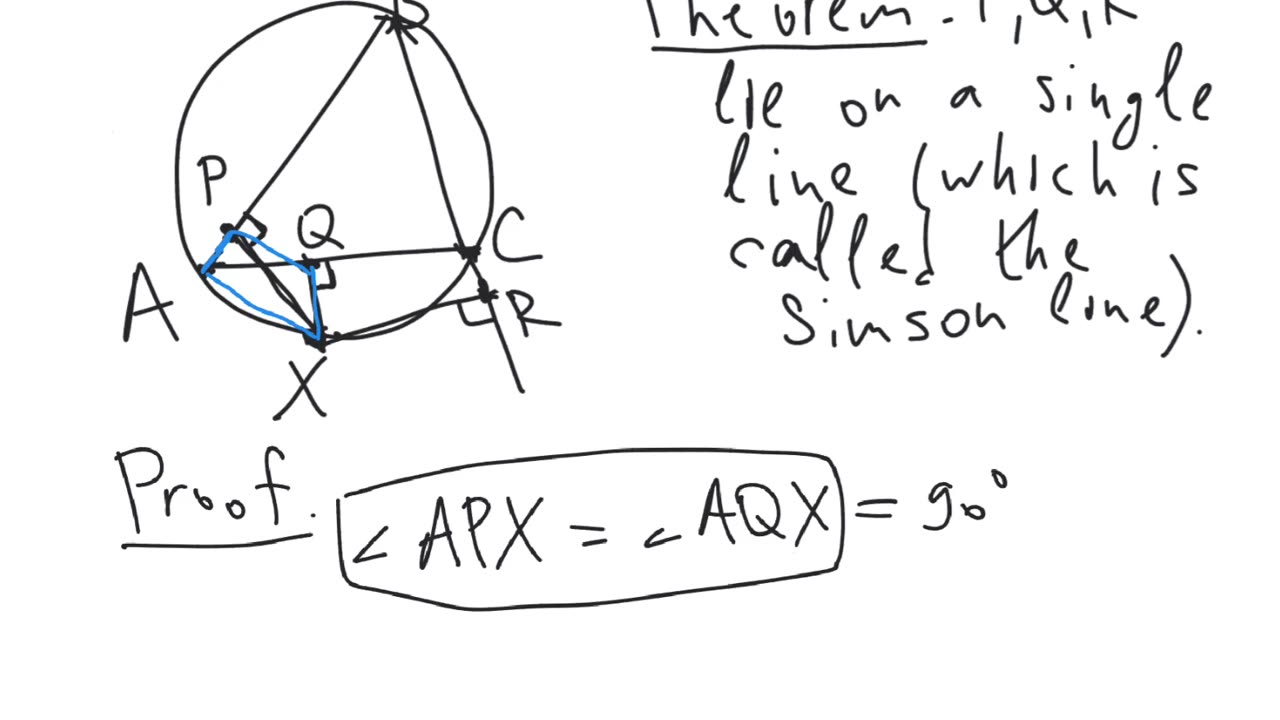
The Simson line | plane geometry | intermediate level

Episode 99.

The Simson line | plane geometry | intermediate level.

Branch of mathematics: plane geometry.
Difficulty level: intermediate.

Theorem. The feet of the altitudes from an arbitrary point on a circumcircle of a triangle to the lines containing the sides of that triangle lie on a single line (which is called the Simson line).

Theorem. Let $ABC$ be a triangle. Let $X$ be an arbitrary point on the circumcircle of the triangle $ABC$. Let $XP$, $XQ$, $XR$ be the altitudes from $X$ to the lines $AB$, $BC$, $CA$ respectively. Then the points $P$, $Q$, $R$ lie on a single line (which is called the Simson line).

Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry

tags:
mathematics,geometry,plane geometry,classical geometry,Euclidean geometry,triangle,line,circle,circumcircle,altitude,perpendicular,collinear,Simson,Simson line

The same video on YouTube:
https://youtu.be/J6bQaWAXJUg

The same video on Telegram:
https://t.me/mathematical_bunker/122