Premium Only Content
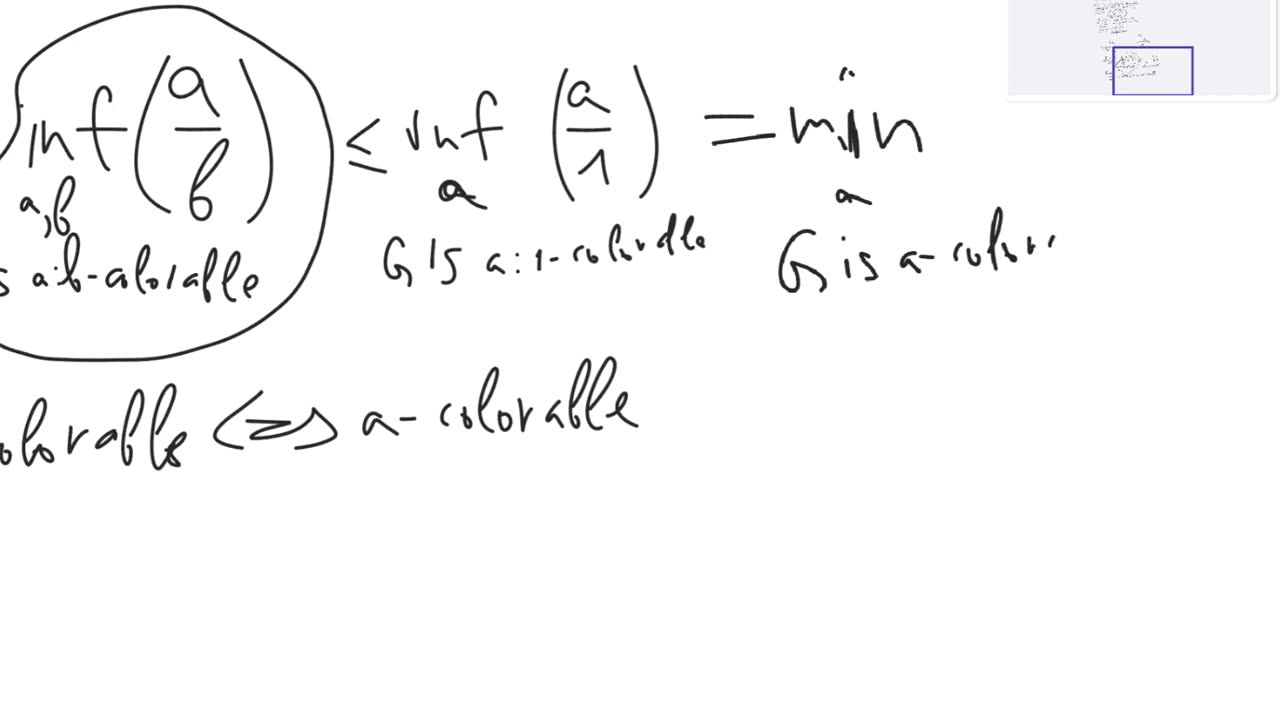
Fractional colorings and the fractional chromatic number of graphs | graph theory | advanced level
Episode 56.
Fractional colorings and the fractional chromatic number of graphs | graph theory | advanced level.
Branch of mathematics: graph theory.
Difficulty level: advanced.
Definition. A fractional $a:b$-coloring of graph $G$ is an assignment of a set of $b$ colors to each vertex of $G$ out of the total of $a$ colors such that for any two adjacent vertices their sets of colors are disjoint.
Definition. A graph is said to be fractionally $a:b$-colorable if there exists a fractional $a:b$-coloring of it.
Definition. The fractional chromatic number of graph $G$, denoted by $\Chi_f(G)$, is $inf_{a,b, \text{$G$ is fractionally $a:b$-colorable}}{\frac{a}{b}}$.
Theorem. For any graph $G$, the fractional chromatic number is less or equal than the chromatic number: $\Chi_f(G) \leq \Chi(G)$.
Theorem. There exists a graph with fractional chromatic number strictly less than the chromatic number.
An example of such a graph is $C_5$, the cycle of length 5. We have $\Chi_f(C_5) \leq \frac{5}{2} < 3 = \Chi(C_5)$.
Mathematics. Discrete Mathematics. Combinatorics. Graph theory.
#Mathematics #DiscreteMathematics #Combinatorics #GraphTheory
The same video on YouTube:
https://youtu.be/0mPbj8vkJek
The same video on Telegram:
https://t.me/mathematical_bunker/80
-
 5:31:43
5:31:43
EricJohnPizzaArtist
4 days agoAwesome Sauce PIZZA ART LIVE Ep. #70: Movie Night featuring Dark Helmet!
37.4K8 -
 2:06:00
2:06:00
Joker Effect
4 hours agoMASSIVE UPDATES ON MY CHANNEL... what does 2026 look like? CHATTIN WITH WVAGABOND (The Captain).
22K2 -
 2:24:34
2:24:34
vivafrei
15 hours agoEp. 292: Bondi's Betrayal & Comey Judge Caught Lying! Crooks Acted Alone? Judicia Activism & MORE!
201K170 -
 8:06:14
8:06:14
GritsGG
9 hours ago#1 Most Warzone Wins 4015+!
142K2 -
 5:14:53
5:14:53
Due Dissidence
12 hours agoTrump SMITTEN By Mamdani, MTG RESIGNS, Hurwitz DOUBLES DOWN on CENSORSHIP, RFK Jr "Poetry" EXPOSED
36.4K32 -
 39:40
39:40
Tactical Advisor
9 hours agoUnboxing New Tactical Packs | Vault Room Live Stream 046
75.6K6 -
 3:30:58
3:30:58
elwolfpr
7 hours agoElWolfPRX Enters the Storm: First Winds
20.7K -
 14:59
14:59
MetatronHistory
23 hours agoAncient Bronze Was Not the Way You Think
44.3K16 -
 LIVE
LIVE
Misfit Electronic Gaming
9 hours ago $1.14 earned"LIVE" WolfPack hunting "ARC RAIDERS" Come Hang out with me.
43 watching -
 5:36:21
5:36:21
DeadMomAlive
12 hours agoSuper Hero Sundays Wonder Woman! BIRTHDAY WEEK!!!!!
29.6K2