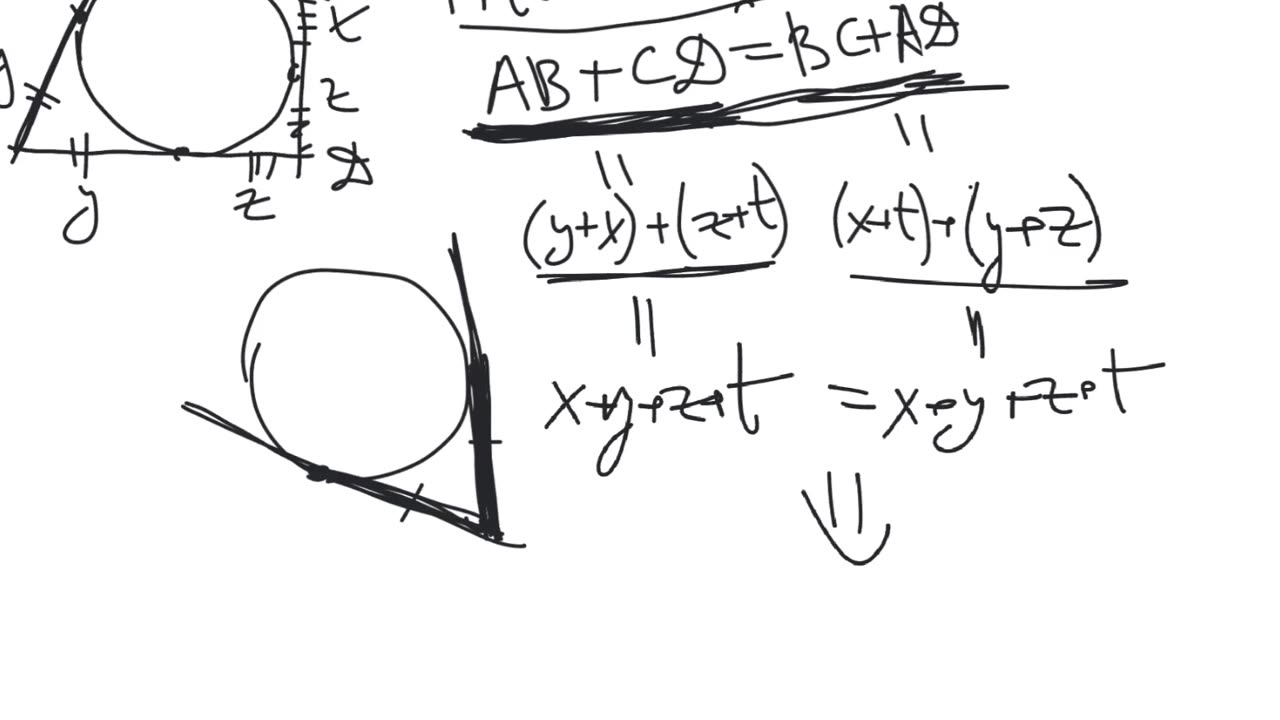
Tangential quadrilaterals, the sums of opposite sides, Pitot's theorem | plane geometry | elementary

Episode 54.

Tangential quadrilaterals, the sums of opposite sides, Pitot's theorem | plane geometry | elementary.
Tangential quadrilaterals (= circumscribed quadrilaterals) and the sums of their opposite sides (Pitot's theorem) | plane geometry | elementary level.

Branch of mathematics: plane geometry.
Difficulty level: elementary.

Definition. A quadrilateral is said to be tangential (or circumscribed) if there exists a circle that touches all of its sides (all of its sides are tangents to this circle).
Pitot's theorem. If a quandrilateral $ABCD$ if tangential, then the sums of its opposite sides are equal to each other, that is, $AB+CD=BC+DA$.
Theorem (the converse statement to the Pitot's theorem). If, for a quadrilateral $ABCD$, we have $AB+CD=BC+DA$, then it is tangential.

Mathematics. Geometry. Plane geometry.
#Mathematics #Geometry #PlaneGeometry

The same video on YouTube:
https://youtu.be/yS5SxIOjOno

The same video on Telegram:
https://t.me/mathematical_bunker/78