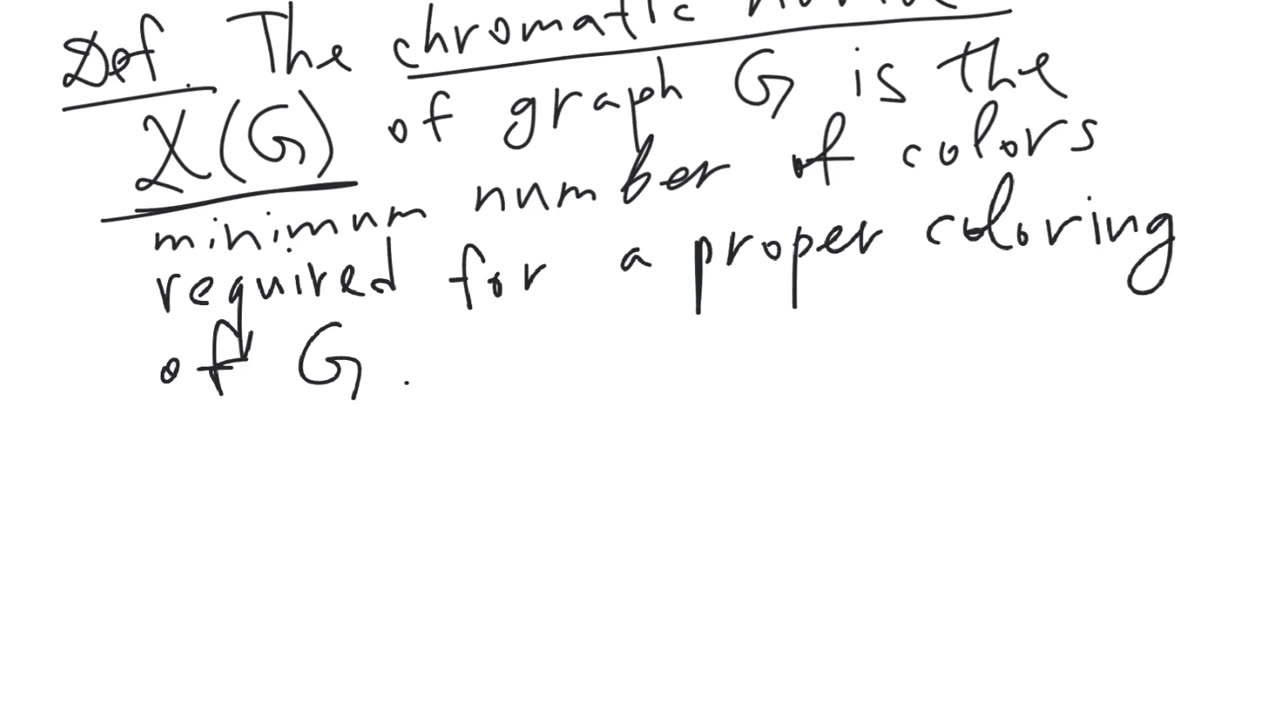
Proper colorings and the chromatic number of graphs | graph theory | elementary level

Episode 51.

Proper colorings and the chromatic number of graphs | graph theory | elementary level.

Branch of mathematics: graph theory.
Difficulty level: elementary.

Definition. A coloring of vertices of a graph is said to be proper if any 2 adjacent vertices are colored in different colors.
Definition. A graph is said to be $r$-colorable if there exists a proper coloring of this graph in $r$ colors.
Definition. The chromatic number of a graph $G$, denoted by $\Chi(G)$, is the minimum number of colors for which there exists a proper coloring of the graph $G$.

The chromatic number of a graph is equal to 1 if and only if it has no edges.
The chromatic number of $K_n$ (the complete graph on $n$ vertices) is equal to $n$.
For all other graphs, the chromatic number is somewhere in between: $1 \leq \Chi(G) \leq n$, where $n$ is the number of vertices of $G$.
The bipartite graphs are 2-colorable and so their chromatic number is less or equal than 2.

Mathematics. Discrete Mathematics. Combinatorics. Graph theory.
#Mathematics #DiscreteMathematics #Combinatorics #GraphTheory

The same video on YouTube:
https://youtu.be/JCo_1v6cF0U

The same video on Telegram:
https://t.me/mathematical_bunker/75