Premium Only Content
This video is only available to Rumble Premium subscribers. Subscribe to
enjoy exclusive content and ad-free viewing.
Ore's theorem about Hamiltonian graphs | graph theory
1 year ago
24
Health & Science
mathematics
graph
graph theory
combinatorics
discrete mathematics
Hamiltonian
Hamiltonian cycle
cycle
Hamiltonian graph
Ore
Episode 41.
Ore's theorem about Hamiltonian graphs | graph theory.
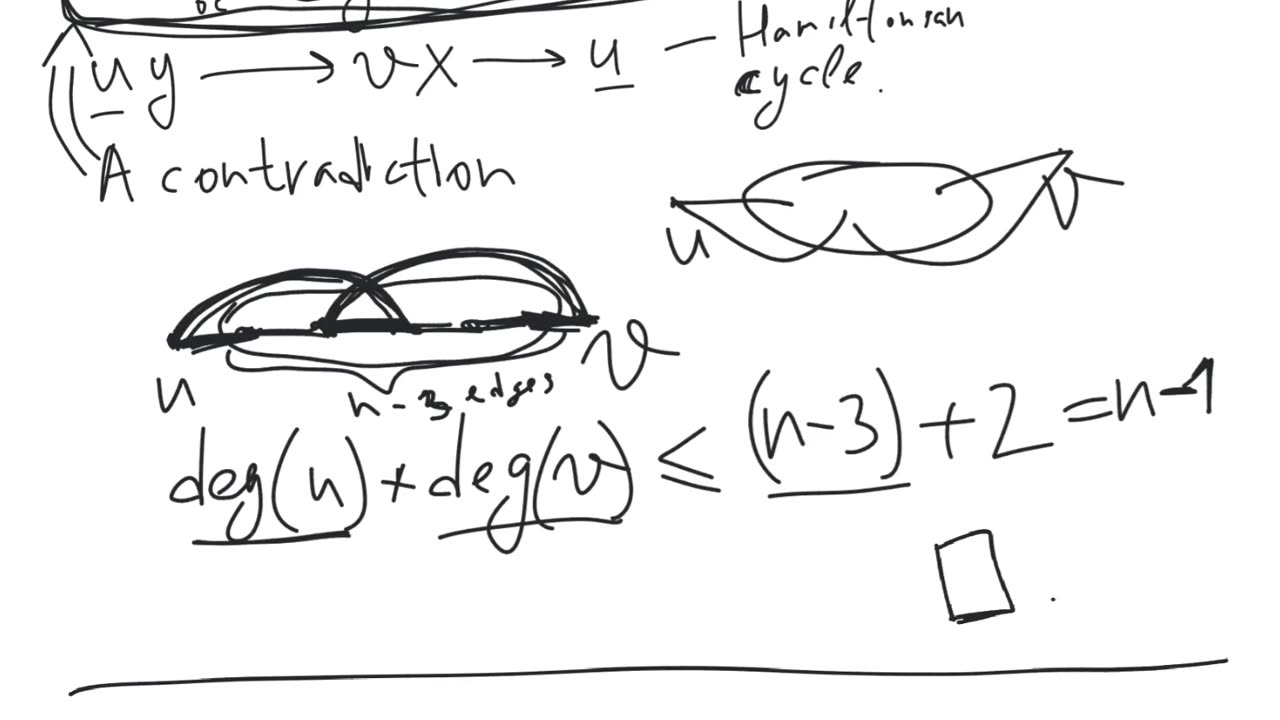
Definition. A Hamiltonian cycle in a graph is a cycle that passes through all vertices of the graph.
Definition. A graph is said to be Hamiltonian if it has a Hamiltonian cycle.
Ore's theorem. For any graph $G$ on $n$ vertices, where $n \geq 3$, if for any pair of non-adjacent vertices $u$ and $v$ we have $deg(u) + deg(v) \geq n$, then the graph $G$ is Hamiltonian.
Mathematics. Discrete Mathematics. Combinatorics. Graph theory.
#Mathematics #DiscreteMathematics #Combinatorics #GraphTheory
The same video on YouTube:
https://youtu.be/Fm4Wr-RjT2M
The same video on Telegram:
https://t.me/mathematical_bunker/65
Loading comments...
-
 23:46
23:46
iCkEdMeL
1 hour ago $1.18 earned🔴 Anna Kepner Case: 3AM Warning and Cabin Screaming Reveal Terrifying Timeline
2.36K -
 LIVE
LIVE
HomieQuest
4 hours agoLive Streaming!
70 watching -
 26:47
26:47
Degenerate Jay
5 hours ago $2.51 earnedPlaying Fallout 3 For The First Time Ever - Here's My Thoughts
12.6K2 -
 LIVE
LIVE
ItsMossy
1 hour ago🍃DEVS ARE CRACKING DOWN🍃maybe a video?🍃shrooms aren't real dude🍃ARC RAIDERS RAIDERING SO HARD🍃
32 watching -
 59:25
59:25
Jeff Ahern
3 hours ago $9.74 earnedThe Saturday Show with Jeff Ahern
75.7K15 -
 29:53
29:53
Afshin Rattansi's Going Underground
2 days agoBRICS MUST Replace the US’ Authoritarian International Financial System! (Prof. Steve Keen)
10.3K16 -
 31:27
31:27
Robbi On The Record
3 days ago $11.40 earnedWhat the Bible say about Astrology.. The Conversation Culture Has Been Avoiding | ft. JT Follows JC
44.9K10 -
 17:38
17:38
Professor Nez
4 hours ago🚨THIS IS A NATIONAL SECURITY EMERGENCY: Stephen Miller with CHILLING WARNING for AMERICA
44.2K110 -
 LIVE
LIVE
tminnzy
3 hours agoBLACK OPS 7 MULTIPLAYER ROAD TO MASTER PRESTIGE
86 watching -
 47:10
47:10
The Rubin Report
8 hours agoWhat Really Happened on ‘The View’ & ‘Curb Your Enthusiasm’ | Cheryl Hines
191K49