Premium Only Content
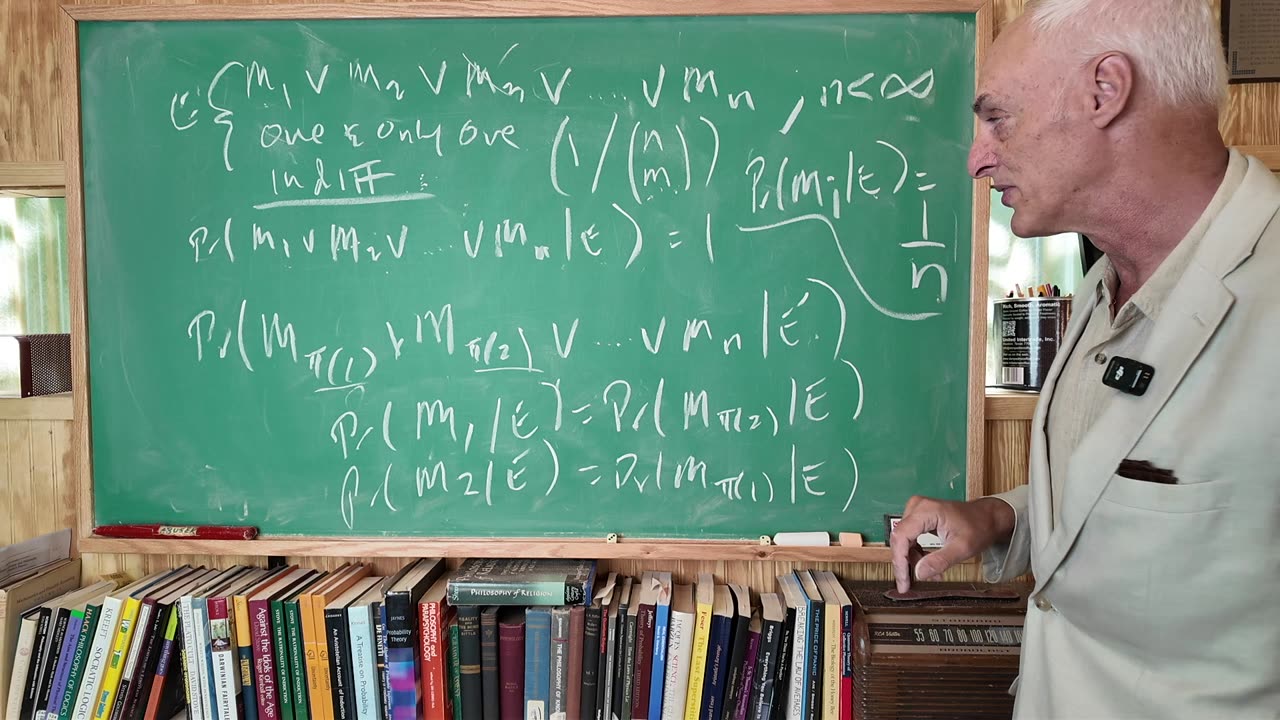
Class 13: No "Fair" Dice & Jaynes Symmetry
Lesson 13: No "Fair" Dice & Jaynes Symmetry
Uncertainty & Probability Theory: The Logic of Science
We learn that adding "fair" to the evidence of a die toss gives a circular argument: it assumes what it sets out to prove, that the probability is symmetric. We examine Jaynes's attempt to provide a proof of equi-probability, but we see that fails because of the same circularity. So does a proof by Diaconis, which you can read on the blog. Next time we do Stove's proof - which works!
Homework: We did Pr(M_6|E) = 1/6, and we did Pr(M_6|E + "fair") = 1/6 (a circular argument!). Now give us Pr(M_6|E + "unfair") = ?
The Infamous Coin Flipping Machine!
https://youtu.be/8XX0iRAN--8
All questions will be answered in the following Monday's lecture.
Written lecture: https://www.wmbriggs.com/post/51979/
https://wmbriggs.substack.com/
Permanent class page: https://www.wmbriggs.com/class/
-
 9:26
9:26
Jamesons Travels
1 day agoShawn Ryan CLOWNS Intel Expert & It GETS WEIRD!
6.89K2 -
 LIVE
LIVE
Jewels Jones Live ®
21 hours agoTRUMP'S GOLDEN AGE | A Political Rendezvous - Ep. 105
1,320 watching -
 1:14:28
1:14:28
Michael Franzese
12 hours agoThe Hidden Cause of LA's Deadliest Fires in 2025?
39.4K79 -
 3:59:45
3:59:45
Bitcoin Sports Network
5 hours agoMax & Stacy Invitational Day 2 Part 1 - LIVE from El Salvador
75.3K8 -
 1:34:30
1:34:30
The Criminal Connection Podcast
5 days ago $1.47 earnedEL PACO: Gypsy Family Wars, Bare Knuckle Boxing, Assassinations and Spirits!
26.8K -
 51:43
51:43
Brewzle
1 day agoI Found Some AWESOME Stores Bourbon Hunting in Des Moines, IA
28K1 -
 1:16:54
1:16:54
Kyle Rittenhouse Presents: Tactically Inappropriate
22 hours ago $1.44 earnedReplacing Matt Gaetz Pt. 2
14.6K8 -
 16:08
16:08
inspirePlay
23 hours ago $0.51 earnedCan You Sniff Out the Golf Imposters Before They Wreck the Score?
13.2K3 -
 22:57
22:57
RTT: Guns & Gear
20 hours ago $3.43 earnedPSA Dagger vs. Bear Creek Arsenal BC-102 | The Better Pistol For The Poors
39.4K10 -
 8:28
8:28
MichaelBisping
7 hours agoBISPING: "Islam WILL RETIRE after UFC 311!?" | Makhachev Wants Belal or Shavkat at WELTERWEIGHT
22.1K4