Name: Laboratory Project: Logistic Sequences
Uploaded: 2022-12-15T19:22:31+00:00
Duration: 21 min 58 s
Description: In this video I go over some mathematics for a change after going all year working on my game changing #AntiGravity Part 6 video. In this video I look at the “Laboratory Project” on Logistic Sequences

1 year ago

family friendly matheasy math easy easymath easy math math online calculator calculator free calculator online tools free online tools

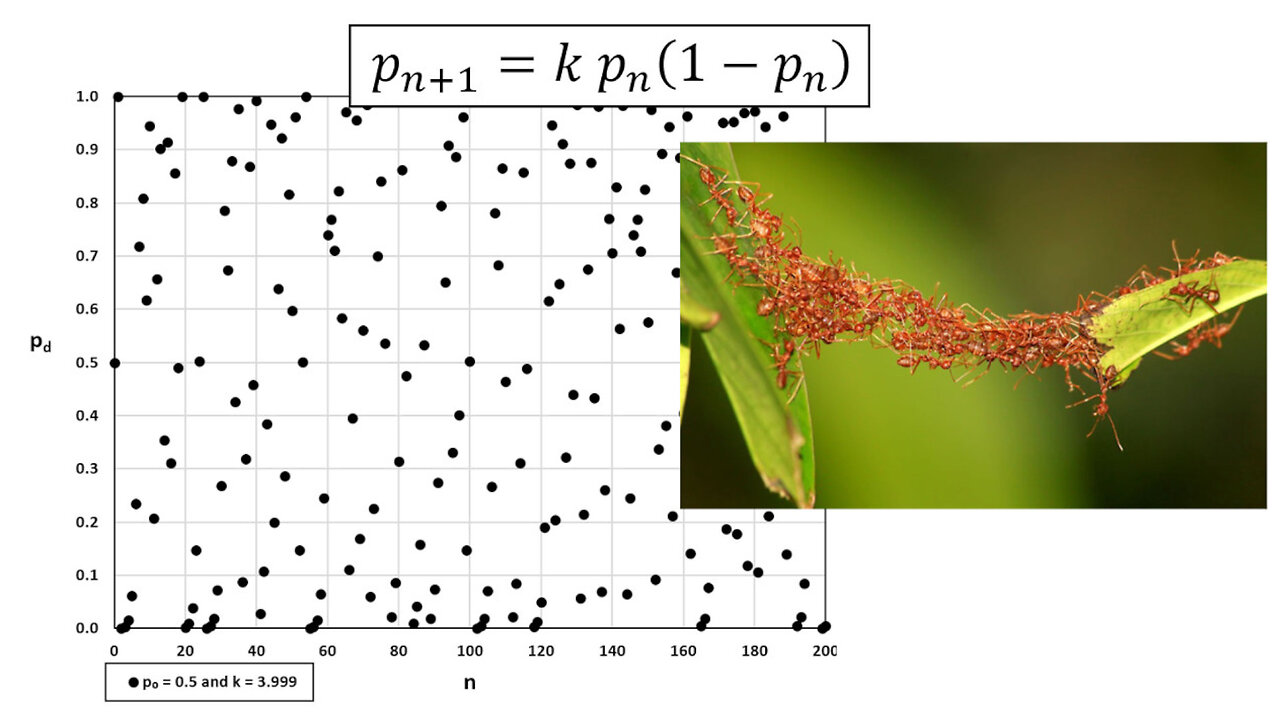
In this video I go over some mathematics for a change after going all year working on my game changing #AntiGravity Part 6 video. In this video I look at the “Laboratory Project” on Logistic Sequences; note that laboratory projects are very interesting math projects at the end of some sections in my calculus book titled Early Transcendentals by James Stewart. The logistic sequence is defined by the logistic difference equation:

Current population = (a constant k) * (previous population)*(1 – previous population)

Note that this equation is similar to the logistic differential equation which I covered earlier and is given by the following formula.

Population growth = (a constant k) * population (1 – population / carrying capacity K)

The logistic sequence involves individual discrete values for the population size and is often preferred for modeling insect populations where mating and death occur periodically. In this project I take a look at modeling the logistic equation using Microsoft Excel spreadsheet to compare how the populations change with changing initial populations and constant k. Interestingly for some values of k there appears to be a leveling off of the population into 1 or more branches. But for other larger values of k the model gives very chaotic and spread out values for the population. The link to the Excel sheet is listed below so make sure to download it and play around with the logistic sequence model!

Download the notes in my video:

PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIh8N8XBPGW5vi1TjDKw
Excel File: https://1drv.ms/x/s!As32ynv0LoaIh8N-Iy9FpTaG99wgJA?e=vQl3RQ

View video notes on the Hive blockchain: https://peakd.com/mathematics/@mes/laboratory-project-logistic-sequences