Premium Only Content
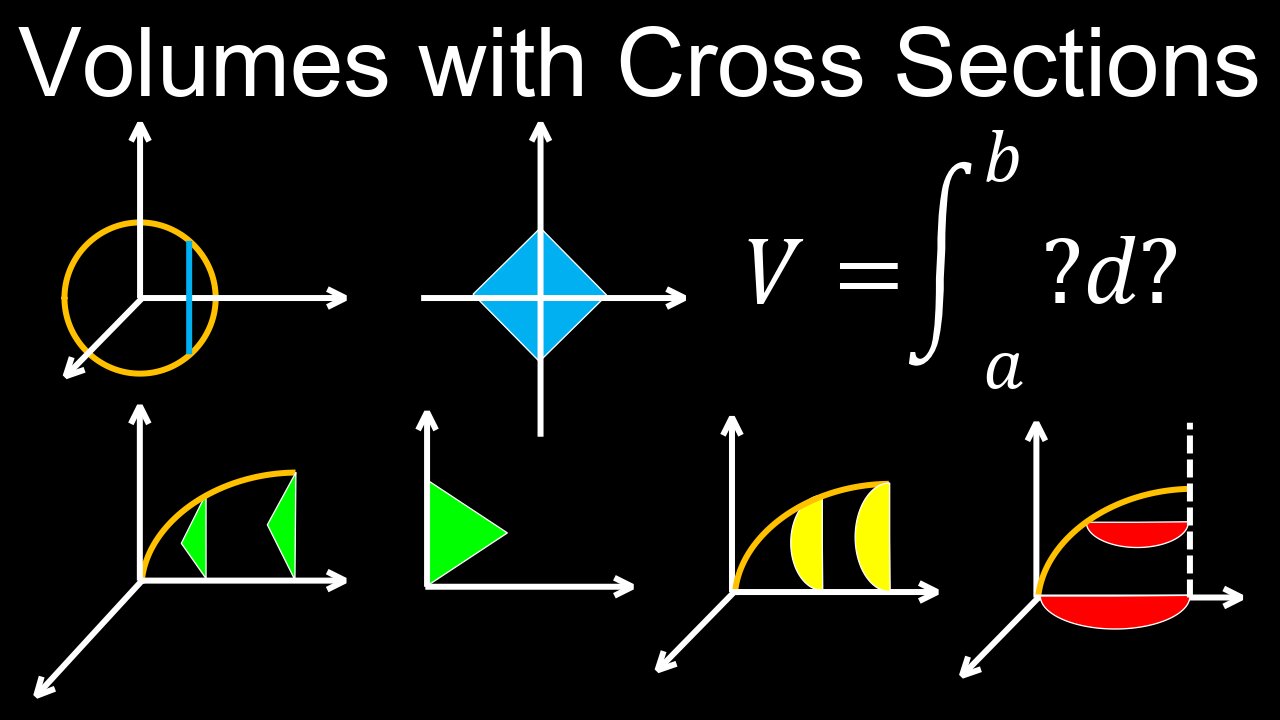
Volumes with Cross Sections, Squares, Rectangles, Triangles and Semicircles - Calculus
In calculus, volumes using cross-sections are found by integrating the area of a slice across a region, expressed as \(V=\int _{a}^{b}A(x)\,dx\) or \(V=\int _{c}^{d}A(y)\,dy\). To use this method, you must: 1) Determine the base of the solid and the shape of its cross-sections perpendicular to an axis (e.g., squares, rectangles, triangles), 2) Find the formula for the area, \(A\), of one cross-section in terms of the integration variable (e.g., \(A(x)\)), and 3) Integrate this area function over the appropriate bounds to sum the volumes of all the infinitesimal slices, yielding the total volume.
💡Steps for Calculating Volume with Cross-Sections
• Sketch the Solid and Its Base: Start by sketching the region that forms the base of the solid and the shape of its cross-sections.
• Identify the Cross-Sectional Area Function:
⚬ Choose the variable of integration (either \(x\) or \(y\)).
⚬ Determine the formula for the area, \(A\), of a single cross-section based on the shape of that slice (e.g., \(A=s^{2}\) for a square).
⚬ Express this area, \(A(x)\) or \(A(y)\), as a function of only that chosen integration variable.
• Determine the Limits of Integration: Find the upper and lower bounds (\(a\) and \(b\), or \(c\) and \(d\)) for your integration based on the region of the base.
• Set up and Evaluate the Integral:
⚬ The volume is then given by the definite integral: \(V=\int _{a}^{b}A(x)\,dx\) or \(V=\int _{c}^{d}A(y)\,dy\).
⚬ Evaluate the integral to find the total volume of the solid.
💡Example: Square Cross-Sections
• If the base is a region bounded by curves, and the cross-sections perpendicular to the x-axis are squares, the area \(A(x)\) of a cross-section is the square of the side length, \(s(x)\), found from the base.
• So, \(A(x)=[s(x)]^{2}\).
• The volume is then \(V=\int _{a}^{b}[s(x)]^{2}\,dx\), where \(a\) and \(b\) are the limits along the x-axis.
💡Key Concept:
• Infinite Summation: This method works by approximating the volume as a sum of infinitely many thin slices (each with volume Area × thickness) and then using the definite integral to find the exact sum.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1GQtYzPXeZpvnm7EdpOAPfEyr-VSltAse/view?usp=drive_link
• Answers: https://drive.google.com/file/d/1urkbDfPaDPsymE8T58TZZJHgeUw-P-qx/view?usp=drive_link
💡Chapters:
00:00 Volumes with cross sections, squares and rectangles, with example
02:41 Triangle and semicircle cross sections, with examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 17:59
17:59
GritsGG
13 hours ago15 Win Streak on Warzone! Journey to 4000 Wins!
4.31K -
 7:40
7:40
Blabbering Collector
2 days agoLEAKED: Draco Malfoy, Hooch, Neville Longbottom! | Harry Potter HBO Show Update, Wizarding News
39.5K3 -
 LIVE
LIVE
Lofi Girl
3 years agolofi hip hop radio 📚 - beats to relax/study to
217 watching -
 2:28:53
2:28:53
Inverted World Live
9 hours agoMurder Tourism, Truth Police, & ChatGPT Weddings | Ep. 141
249K13 -
 2:58:44
2:58:44
TimcastIRL
9 hours agoTrump DOJ Opens Probe Into Democrat Swalwell For Mortgage Fraud | Timcast IRL
216K156 -
 2:51:50
2:51:50
Laura Loomer
8 hours agoEP156: Trump Sounds The Alarm On The Nigerian Christian Genocide
76.1K72 -
 1:11:27
1:11:27
Flyover Conservatives
1 day agoDAVID GREEN: “God Owns It All”: How Hobby Lobby Thinks About Money, Time & Eternity w/ Bill High | FOC Show
41.1K5 -
 2:39:00
2:39:00
DLDAfterDark
7 hours ago $13.52 earnedThe Armory - God, Guns, and Gear - A Conversation About Preparedness
46.5K4 -
 23:42
23:42
Robbi On The Record
8 hours ago $3.64 earnedMAGA 2.0? BTS of Michael Carbonara for Congress
40.4K6 -
 4:46:47
4:46:47
Drew Hernandez
1 day agoSHAPIRO COOKS HIMSELF: SAYS YOU DON'T DESERVE TO LIVE WHERE YOU GREW UP?
63.5K32