Premium Only Content
Riemann Sums, Formula, Using Calculator, Examples, Practice Problems - Calculus
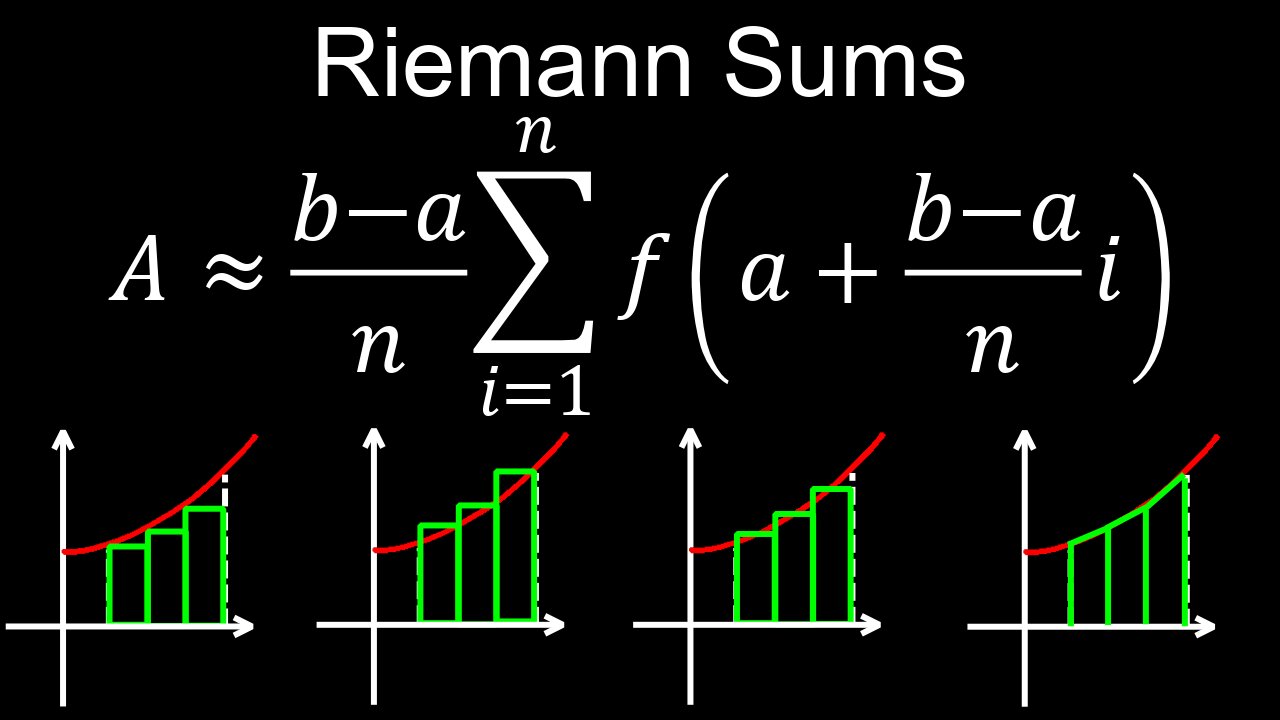
A Riemann sum approximates the area under a curve by dividing the region into a series of rectangles and summing their areas. The width of each rectangle is a subinterval, and its height is determined by evaluating the function at a specific point within that subinterval, such as the left endpoint, right endpoint, or midpoint. By increasing the number of rectangles, the Riemann sum becomes a more accurate approximation of the exact area under the curve, which is found by taking the limit as the number of rectangles approaches infinity.
💡How Riemann Sums Work
• Divide the Interval: The interval over which you want to find the area is divided into smaller, equally-sized subintervals.
• Construct Rectangles: For each subinterval, a rectangle is formed with the x-axis as its base.
• Determine Rectangle Height: The height of each rectangle is found by evaluating the function at a chosen point within its subinterval. Common choices include:
◦ Left Endpoint Rule: The height is determined by the function's value at the left-most point of the subinterval.
◦ Right Endpoint Rule: The height is determined by the function's value at the right-most point of the subinterval.
◦ Midpoint Rule: The height is determined by the function's value at the midpoint of the subinterval.
• Calculate Rectangle Area: The area of each individual rectangle is calculated by multiplying its width (the subinterval's width) by its height.
• Sum the Areas: The Riemann sum is the total of the areas of all these rectangles.
💡The Relationship to Integration
• A Riemann sum is an approximation of the definite integral. As the number of rectangles increases, the approximation becomes more precise. When the number of rectangles approaches infinity, the Riemann sum converges to the exact area under the curve, which is the value of the definite integral.
💡Purpose of Riemann Sums
• Approximation: Riemann sums provide a way to estimate the area under a curve when an exact antiderivative might be difficult or impossible to find.
• Foundation of Integration: They serve as a fundamental concept in calculus, illustrating how a continuous function's area can be broken down and added up.
• Building Intuition: By visualizing the process of subdivision, approximation, and summation, Riemann sums help in understanding the underlying principles of integral calculus.
💡Worksheets are provided in PDF format to further improve your understanding:
• Questions Worksheet: https://drive.google.com/file/d/1nyZAxMFIv3phTs8a9uQiZ7WKvrQ4fBKt/view?usp=drive_link
• Answers: https://drive.google.com/file/d/16wbbNzLH-O0LGu6SEvM5Nq9gNQlpoR-H/view?usp=drive_link
💡Chapters:
00:00 Intro to Riemann sums
01:26 Left Riemann sum
02:42 Right Riemann sum
03:33 Midpoint Riemann sum
04:47 Trapezoidal sum
06:20 Worked examples
🔔Don’t forget to Like, Share & Subscribe for more easy-to-follow Calculus tutorials.
🔔Subscribe: https://rumble.com/user/drofeng
_______________________
⏩Playlist Link: https://rumble.com/playlists/Ptm8YeEDb_g
_______________________
💥 Follow us on Social Media 💥
🎵TikTok: https://www.tiktok.com/@drofeng?lang=en
𝕏: https://x.com/DrOfEng
🥊: https://youtube.com/@drofeng
-
 LIVE
LIVE
ZWOGs
2 hours ago🔴LIVE IN 1440p! - ARC RAIDERS SERVER SLAM - Come Hang Out!
44 watching -
 9:22
9:22
Colion Noir
8 hours agoArmed Woman Drags Gunman Out of Store Before Firing Two Shots
79.7K40 -
 1:04:17
1:04:17
Jeff Ahern
4 hours ago $1.23 earnedThe Saturday Show with Jeff Ahern
22K7 -
 LIVE
LIVE
Reidboyy
5 hours agoCamo King Grinds 100% Completion for Battlefield 6 *SECRET* Mastery Camo (All Badges + Camos 100%)
9 watching -
 LIVE
LIVE
Biscotti-B23
2 hours ago🔴 LIVE NEW INFO ON KAIGAKU & ZENITSU INFINITY CASTLE 🔥 DEMON SLAYER HINOKAMI CHRONICLES 2
7 watching -
 LIVE
LIVE
NeoX5
3 hours agoPixel Art Horror | Shocktober | Rumble Gaming
23 watching -
 44:34
44:34
Chris Harden
2 days ago $1.52 earnedWhat Happened to Rock Island, Illinois?
24.5K12 -
 30:56
30:56
Advanced Level Diagnostics
6 days ago $0.91 earned2004 Chevy Silverado - Won't Shut Off!
24K2 -
 7:05
7:05
Spooky Grandpa's Scary Stories
7 months agoThose Who Linger - Halloween, Ghost Stories, Horror, Haunted, Cemetery, Folklore
18K17 -
 2:23
2:23
Memology 101
1 day ago $1.69 earnedAOC spits completely made-up BULLSH*T during UNHINGED anti-Republican rant
18.6K50